федеральное агентство железнодорожного транспорта
Федеральное государственное бюджетное образовательное учреждение
высшего образования
«Петербургский государственный университет путей сообщения
Императора Александра I»
(ФГБОУ ВО ПГУПС)
Факультет «Автоматизация и интеллектуальные технологии»
Кафедра «Методы и приборы неразрушающего контроля»
Пояснительная записка
к курсовой работе
на тему: «Обработка и обнаружение акустических сигналов»
Обучающийся группы ПБ-613 |
________________ |
Сабитов И.А. |
|
Подпись, дата |
|
Преподаватель |
________________ |
Чурова В.В. |
|
Подпись, дата |
|
|
|
|
Санкт-Петербург
2020
Обозначения и сокращения
с.в. |
- |
случайная величина |
СКО |
- |
среднее квадратическое отклонение |
ФНЧ |
- |
фильтр нижних частот |
ФВЧ |
- |
фильтр верхних частот |
ПФ |
- |
полосовой фильтр |
РФ |
- |
режекторный фильтр |
КИХ |
- |
конечная импульсная характеристика |
АЧХ |
- |
амплитудно-частотная характиристика |
ФЧХ |
- |
фазо-частотная характеристика |
БПФ |
- |
быстрое преобразование Фурье |
Оглавление
1.Исследование параметров случайного процесса 3
Расчет числовых характеристик 3
1.2.Спектральный анализ сигнала 6
2. Выбор метода предварительной обработки сигнала 10
2.1. Этапы разработки цифрового фильтра 10
2.2. Спецификация требований к фильтру 10
2.3. Вычисление коэффициентов фильтра……………………….……………………………………………………………..11
2.4. Реализация фильтра в среде Mathlab………………………………………………………………………………………15
3.Разработка алгоритма обнаружения сигнала 18
4.Разработка блок-схемы устройства цифровой обработки сигнала 23
4.1. Расчет параметров аналого-цифрового тракта. 24
4.2. Расчет объема внутренней памяти для хранения данных 25
Список рекомендуемой литературы 26
1 Исследование параметров случайного процесса
Числовые параметры (числовые характеристики) позволяют с помощью небольшого набора чисел охарактеризовать основные особенности случайного процесса. К числовым характеристикам случайных величин (с.в.) относятся: математическое ожидание, мода, медиана, начальные и центральные моменты, среднее квадратическое отклонение (СКО) и т.д. Математическое ожидание и дисперсия (или СКО) – чаще всего применяемые числовые характеристики. Когда числовые характеристики определяются по опытным данным ограниченного объема, используют понятие оценки числовой характеристики, т.е. ее приближенного значения.
1.1 Расчет числовых характеристик
1.1 Расчет числовых характеристик
Оценка
для математического ожидания 
дискретного сигнала
|
(1.1) |
Оценка
дисперсии
рассчитывается
по выражению
|
(1.2) |
Среднее квадратическое отклонение
= |
(1.3) |
Энергия сигнала по временной области
|
(1.4) |
В таблице 1.1 приведены результаты расчета параметров исходного сигнала по выражениям (1), (2), (3) и (4).
Таблица 1.1 – Числовые параметры исходного сигнала
Параметр сигнала |
Значение |
Оценка мат ожидания |
-1.128 · 10-4 |
Оценка дисперсии |
0.0273 |
Оценка СКО |
0.165 |
Энергия сигнала |
6.866 · 103 |
Длительность сигнала |
5.688 |
Текст программы в Matlab для расчета значений таблицы 1.1 и построения графика представленного на рисунке 1.1.
Текстпрограммы clear; clc; fx=load('Data4.txt'); n=length(fx); mx=mean(fx);%мо% s=0; for i=1:n s=s+(fx(i)-mx)^2; end Dx=s/(n-1);%дисперсия% c=sqrt(Dx); E=sum(fx.^2);%энергия% Fd=44100; dt=1/Fd; T=dt*(n-1); y=fx; t=0:dt:T; plot(t,y) title('Зависимость "Амплитуда-время"') xlabel('Время,с'); ylabel('Амплитуда,В'); set(gcf,'color','w'); grid on; y1=mx; y2=mx+c; y3=mx-c; hold on plot([t(1) t(end)],[y1 y1],'r'); plot([t(1) t(end)],[y2 y2],'g'); plot([t(1) t(end)],[y3 y3],'g'); legend('исходный сигнал','Оценка m_x','Оценка \sigma_x'); save('fx.mat', 'fx', 'Fd', 't');
|
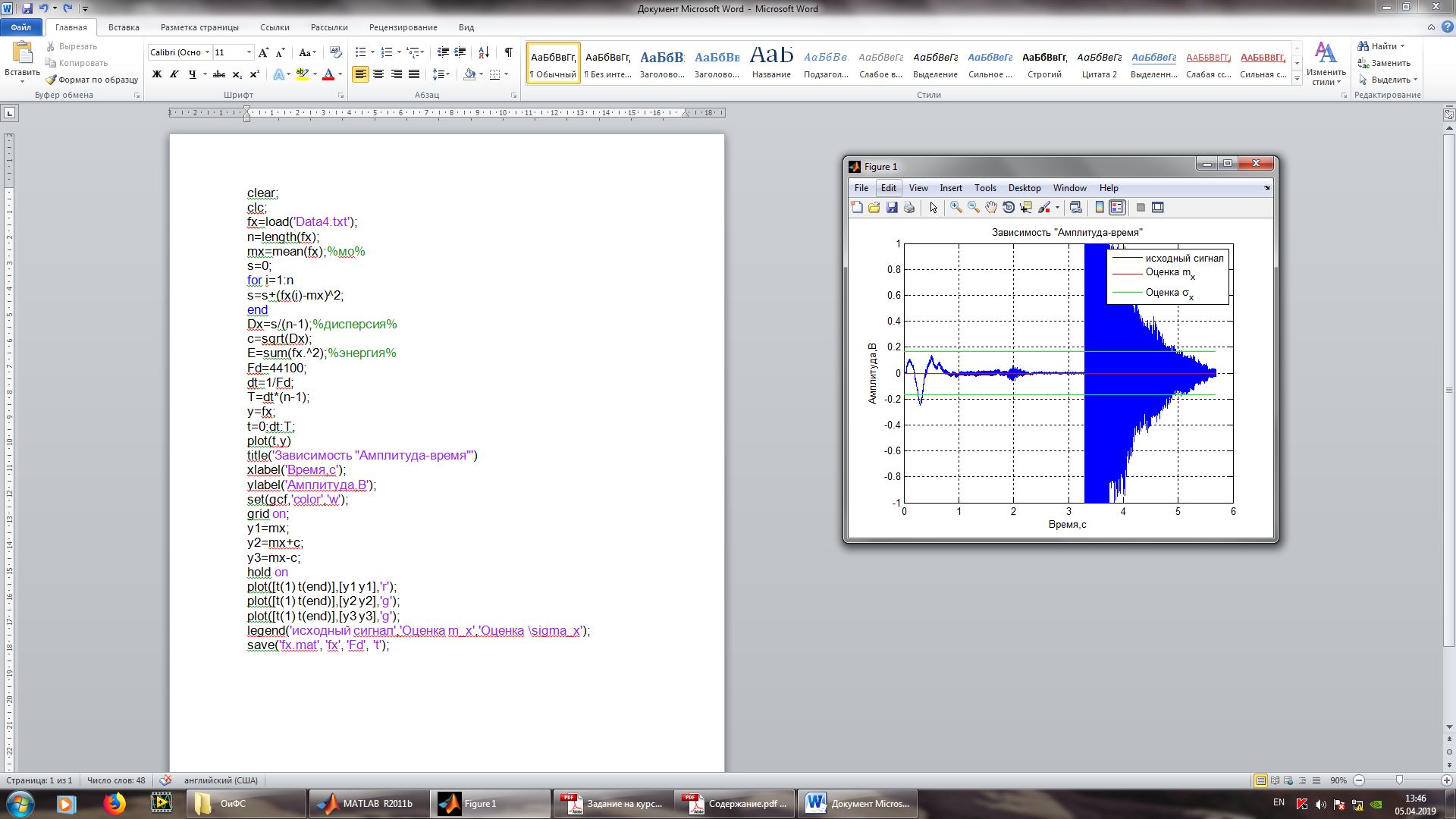
Рисунок 1.1– График исходного сигнала