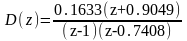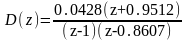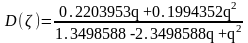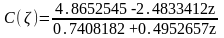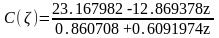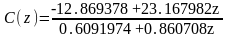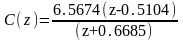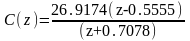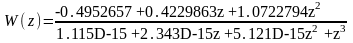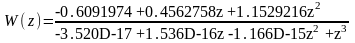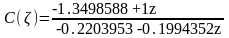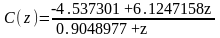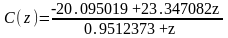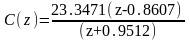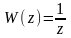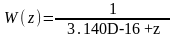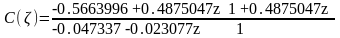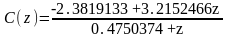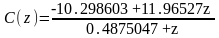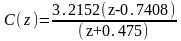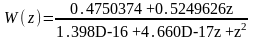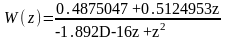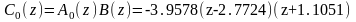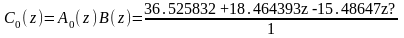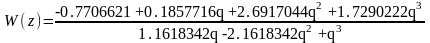Л8

Отчёт по лабораторной работе №8

Синтез цифровых регуляторов методами теории

дискретных систем

Вариант: 13

1. Модель объекта

Непрерывная модель объекта:

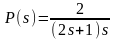
Дискретная передаточная функция объекта (здесь и далее в левом столбце – данные для исходного интервала квантования, справа – для интервала, который в 2 раза меньше заданного):

T = 0.6 с	T = 0.3 c

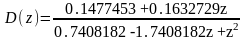
Дискретная передаточная функция объекта в формате «нули-полюса»:

Дискретная передаточная функция объекта в переменной :

2. Апериодическое управление (управление с конечной длительностью переходных процессов

Дискретная передаточная функция цифрового регулятора (от переменной ):

Характеристический полином замкнутой системы (от переменной ):

 () = 1 -1.110D-16q² -1.110D-16q³

 () = 1 +4.441D-16q² +2.220D-16q³

Характеристический полином не совпадает с желаемым.

Дискретная передаточная функция цифрового регулятора (от переменной z):

Дискретная передаточная функция регулятора в формате «нули-полюса»:

Выводы (сокращаются ли регулятором нули и полюса объекта в произведении D(z)·C(z)? Если да, какие именно?):

Сокращаются все, кроме полюса третьей степени.

Сокращаются все, кроме полюса третьей степени.

Характеристический полином замкнутой системы (от переменной z):

 (z) = 0.4952657 +0.7408182z	 (z) = 0.6091974 +0.860708z
Характеристический полином не совпадает с желаемым.

Корни характеристического полинома:

-0.6685388 Система устойчива, потому что корни по модулю меньше 1.

-0.7077864 Система устойчива, потому что корни по модулю меньше 1.

Дискретная передаточная функция замкнутой системы:

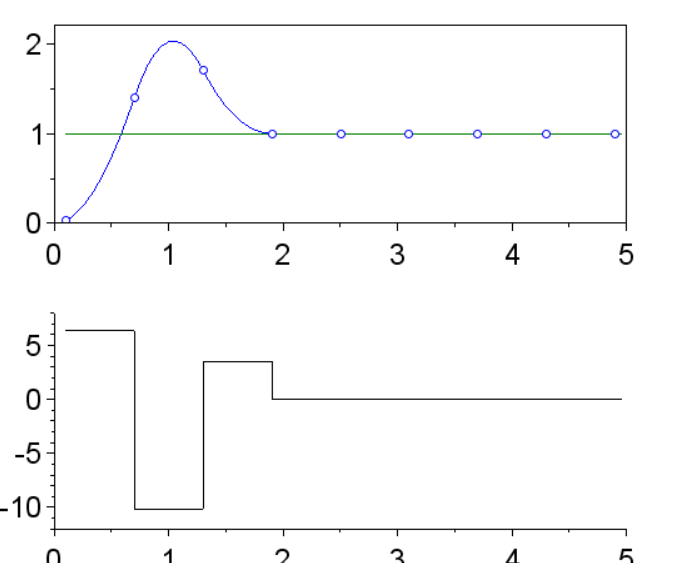
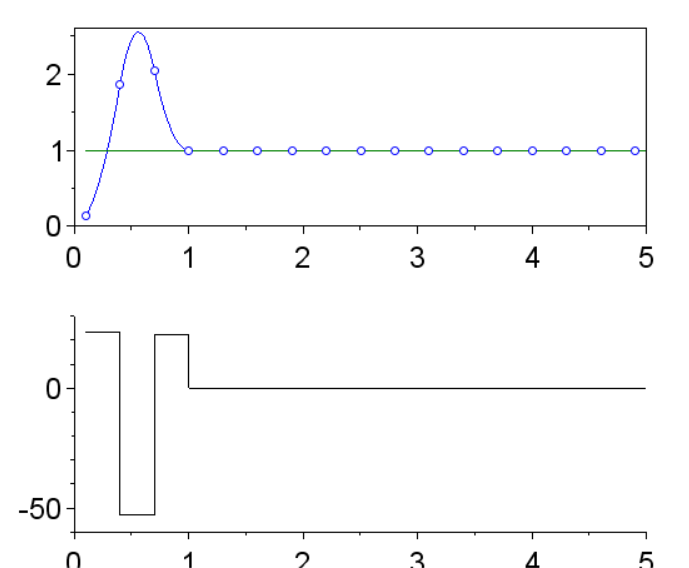
Переходные процессы:

Перегулирование и время переходного процесса:

 = 102.47857 %, tпп = 1.78 c.

 = 155.19142 %, tпп = 0.94 c.

Выводы:

1) обеспечивается ли переходный процесс с конечной длительностью?

2) для двух интервалов квантования сравните а) величину сигнала управления; б) перерегулирование; в) время переходного процесса.

2. Процессы минимальной длительности

Модель входного сигнала:

Дискретная модель входного сигнала:

Цифровой регулятор, обеспечивающий процесс минимальной длительности:

Дискретная передаточная функция регулятора в формате «нули-полюса»:

Выводы (сокращаются ли регулятором нули и полюса объекта в произведении D(z)·C(z)? Если да, какие именно?):

Сокращаются все, кроме старшей степени.

Сокращаются все, кроме старшей степени.

Характеристический полином замкнутой системы (от переменной z):

(z) = 0.9048977 +z

(z) = 0.9512373 +z

Корни характеристического полинома:

-0.9048977 Система устойчива, потому что корни по модулю меньше 1.

-0.9512373 Система устойчива, потому что корни по модулю меньше 1.

Дискретная передаточная функция замкнутой системы:

Переходные процессы:

Выводы:

Удалось обеспечить процесс с конечной длительностью в моменты квантования.

Есть скрытые колебания.

Уменьшение периода квантования не помогает избавиться от скрытых колебаний

У сигнала управления увеличилась частота моментов квантования.

Что вызывает скрытые колебания (как их можно предсказать?):

Скрытые колебания появляются, когда сокращается пара «нуль-полюс» .

2. Процессы минимальной длительности (без компенсации «опасных» нулей)

Цифровой регулятор, обеспечивающий процесс минимальной длительности:

Дискретная передаточная функция регулятора в формате «нули-полюса»:

Выводы (сокращаются ли регулятором нули и полюса объекта в произведении D(z)·C(z)? Если да, какие именно?):

Сокращаются все, кроме старшей степени

Сокращаются все, кроме старшей степени

Характеристический полином замкнутой системы (от переменной z):

(z) = 0.4750374 +z

(z) = 0.4875047 +z

Корни характеристического полинома:

-0.4750374 Система устойчива, потому что корни по модулю меньше 1.

-0.4875047 Система устойчива, потому что корни по модулю меньше 1.

Дискретная передаточная функция замкнутой системы:

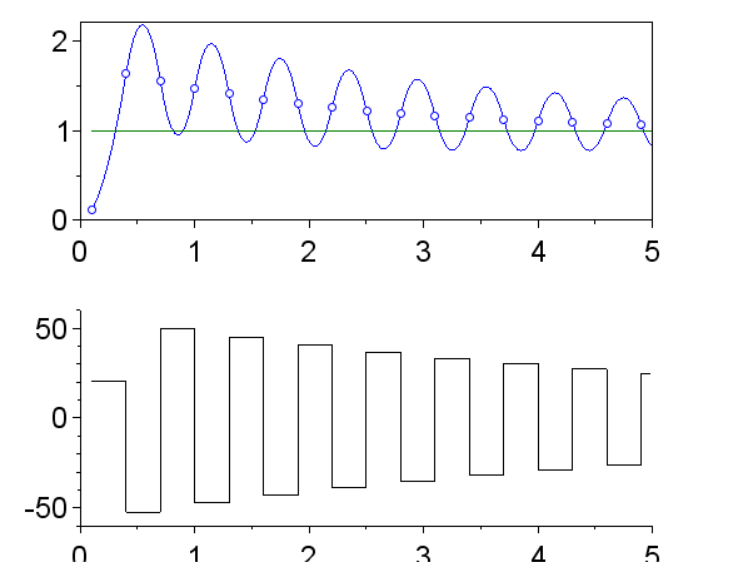
Переходные процессы:

Выводы:

Удалось обеспечить процесс с конечной длительностью в моменты квантования.

Есть скрытые колебания.

В сигнале управления не наблюдается колебаний.

Увеличивается количество моментов колебаний.

2. Синтез цифрового регулятора по эталонной модели

Параметры желаемого переходного процесса:

t_пп = 1 с,  = 15 %

Эталонная модель:

W_m(s) =

Эталонная модель в дискретной форме:

,

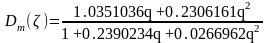
Полиномы регулятора с двумя степенями свободы:

с компенсацией всех устойчивых нулей	без компенсацией «опасных» нулей
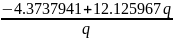
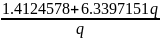
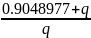
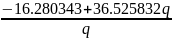
a0() = a1() = b() =	a0() = a1() = b() =

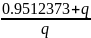
Дискретные передаточные функции блоков регулятора (в плоскости z):

, ,

, ,

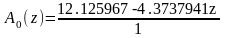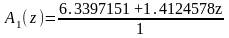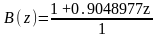
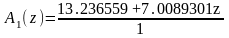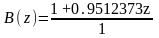
Дискретная передаточная функция регулятора в контуре в формате «нули-полюса»:

Выводы (сокращаются ли регулятором нули и полюса объекта в произведении D(z)·C₀(z)? Если да, какие именно?):

Не сокращаются.

Не сокращаются.

Характеристический полином замкнутой системы (в плоскости z):

 (z) = 1.3498588q -2.3498588q² +q³

 (z) = -15.4865(z-2.2436)(z+1.0513)

Корни характеристического полинома:

1.3498588 + 0.i 1. + 0.i 0. + 0.i Система неустойчива, потому что корни по модулю больше 1.

1.1618342 + 0.i 1. + 0.i 0. + 0.i Система неустойчива, потому что корни по модулю больше 1.

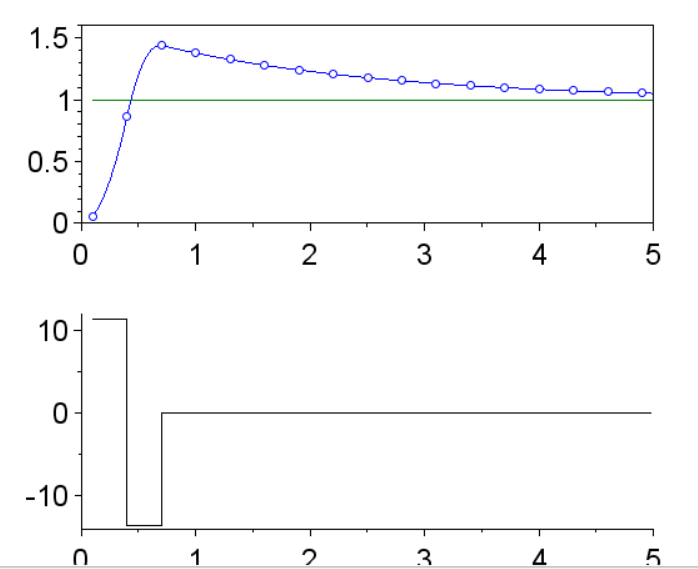
Дискретная передаточная функция замкнутой системы:

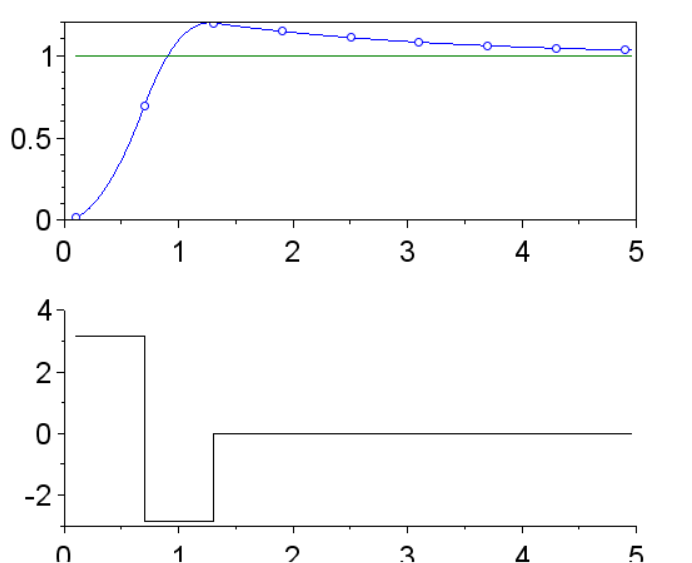
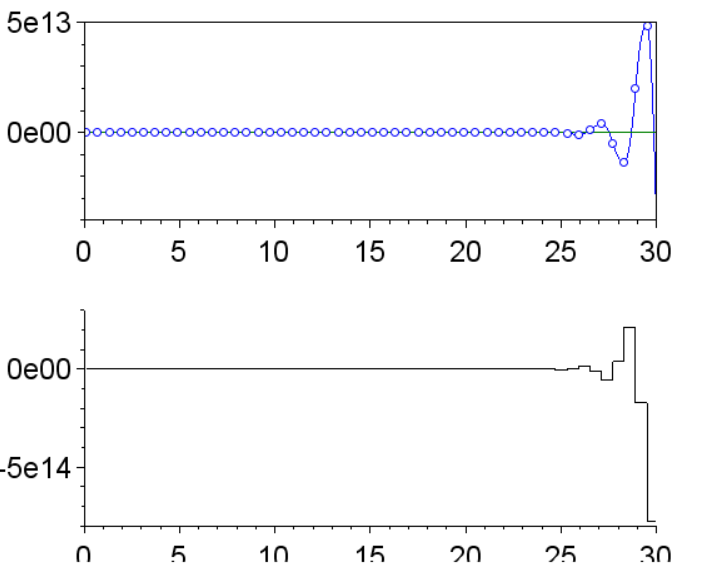
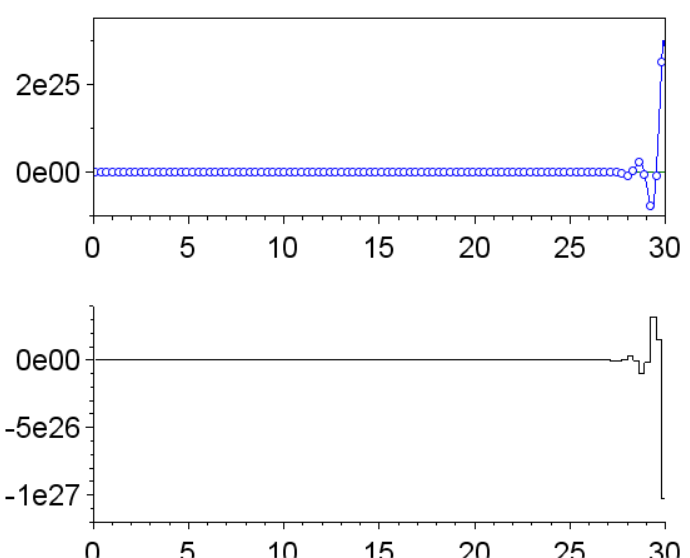
Переходные процессы:

Выводы:

Сравните переходные процессы в двух системах:

Удалось обеспечить соответствие эталонной модели в моменты квантования.

Нет скрытых колебаний.

Сигнал управления колеблется в последнем отрезке интервала.

Что вызывает скрытые колебания (как их можно предсказать?):

Чтобы в построенной системе не было скрытых колебаний, нужно при факторизации просто считать «опасные» нули и полюса (с отрицательными вещественным частями) «неустойчивыми», и не сокращать их