шпоры мехмат / 1.1 Внешние силы и их классификация

Внешняя сила — это мера взаимодействия между телами. В задачах сопротивления материалов внешние силы считаются всегда заданными. К внешним силам относятся также реакции опор (связей). Внешние силы делятся на объемные и поверхностные. Объемные силы при­ложены к каждой частице тела по всему его объему. Примером объемных сил являются силы веса и силы инерции. Часто задают простой закон изменения этих сил по объему. Объемные силы определяются их интенсивностью, как предел отношения равнодействующей сил в рассматриваемом элементарном объеме к величине этого объема, стремящего к нулю: lim V 0 V F и измеряются в Н/м³.

Поверхностные силы делятся на сосредоточенные и распределенные. Сосре­доточенными считаются силы, приложенные к малой поверхности, размеры которой малы по сравнению с размерами тела. Однако при расчете напряжений вблизи зоны приложения силы нагрузку следует считать распределенной. К сосредоточенным нагрузкам относят не только сосредоточенные силы, но и пары сил, примером которых можно счи­тать нагрузку, создаваемую гаечным ключом при закручивании гайки. Сосредоточенные усилия измеряются в кН. Распределенные нагрузки бывают распределенными по длине и по площади . К распределенным нагрузкам относят давление жидкости, газа или другого тела. Распределенные силы измеряются, как правило, в кН/м (распределенные по длине) и кН/м² (распределенные по площади).

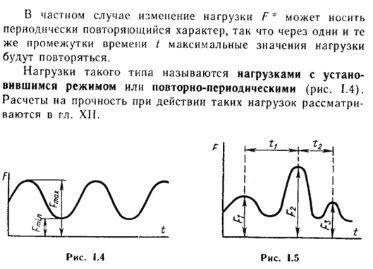
Все внешние нагрузки можно разделить на статические и динамические. Статическими считаются нагрузки, в процессе приложения которых возникающие силы инерции малы и ими можно пренебречь. Если силы инерции велики (к примеру – землетрясение) – нагрузки считаются динамическими. Примерами таких нагрузок также могут служить внезапно приложенные нагрузки, ударные и повторно-переменные. Внезапно приложенные нагрузки передаются на сооружение сразу полной своей величиной (к примеру давление колес локомотива, входящего на мост). Ударные нагрузки возникают при быстром изменении скорости соприкасающихся элементов конструкции, например» при ударе бабы копра о сваю при ее забивке. Повторно-переменные нагрузки действуют на элементы конструкции, повторяясь значительное число раз. Таковы, например, повторные давления пара, попеременно растягивающие и сжимающие шток поршня и шатун паровой машины. Во многих случаях нагрузка представляет собой комбинацию нескольких видов динамических воздействий.

Внутренние силы

В результате действия внешних сил в теле возникают внутренние силы. Внутренняя сила — силы взаимодействия между частями одного тела, возникающие под действием внешних сил.

Внутренние силы являются самоуравновешенными, поэтому они не видны и не влияют на равновесие тела. Определяют внутренние силы методом сечения.

Внешние нагрузки приводят к следующим видам напряженно-деформированного состояния:

• Срез

• Изгиб

• Кручение

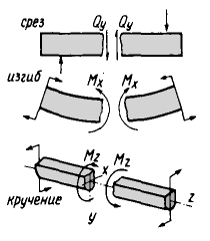
Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.

Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).

Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.

П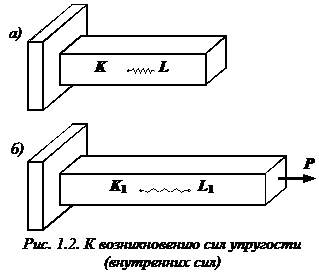 риложим теперь к стержню растягивающую силу  (рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение  , а частица L – в положение  . Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений.

Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.

Разрежем стержень, находящийся в равновесии под действием некоторой системы сил  (рис. 1.3, а) на две части плоскостью, перпендикулярной к его оси z.

Отбросим одну из частей стержня и рассмотрим оставленную часть.

Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменим действие отброшенной части внутренними силами (рис. 1.3, б).

Полученную бесконечную систему сил по правилам теоретической механики можно привести к центру тяжести поперечного сечения. В результате получим главный вектор R и главный момент M (рис. 1.3, в).

Разложим главный вектор и главный момент на составляющие по осям x, y (главные центральные оси) и z.

Получим 6 внутренних силовых факторов, возникающих в поперечном сечении стержня при его деформировании: три силы  (рис. 1.3, г) и три момента  (рис. 1.3, д).

Сила N - продольная сила

– поперечные силамы,

момент относительно оси z ( ) – крутящий момент

моменты относительно осей x, y ( ) – изгибающие моменты.

Запишем для оставленной части тела уравнения равновесия (уравновесим):

.

Из уравнений определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня.