шпоры мехмат / 10.1 Моменты инерции сечений- осевые, полярные, центробежные. Их свойства
.docxОсевым моментом инерции сечения относительно оси x называется сумма произведений элементарных площадок dA на квадрат их расстояний до данной оси, численно равная интегралу
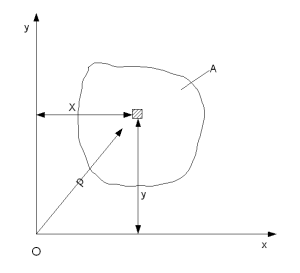
где у — расстояние от элементарной площадки dA до оси х (смотри рисунок), х — расстояние от элементарной площадки dA до оси у.
Полярным моментом инерции сечения относительно данной точки (называемого полюсом ) называется сумма произведений элементарных площадок dA на квадрат их расстояний до этой точки:
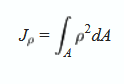где
– расстояние от площадки dA
до полюса, относительно которой
вычисляется полярный момент инерции.
Центробежным моментом инерции сечения относительно осей x и y называется сумма произведений элементарных площадок dA на их расстояния до этих осей:
где
x,у — расстояние от элементарной площадки
dA до осей х и y (смотри рисунок).
Центробежный момент инерции может быть положительным, отрицательным и, в частном случае, равным нулю. Если взаимно перпендикулярные оси x и y или одна из них являются осями симметрии фигуры, то относительно таких осей центробежный момент инерции равен нулю. Jxy=0.
Полярный момент инерции относительно какой – либо точки равен сумме осевых моментов инерции относительно двух взаимно перпендикулярных осей, проходящих через эту точку.
J
=Jx+Jy
Некоторые свойства моментов инерции сечения
Размерность – длина4 ( обычно см4)
Осевой и полярный моменты инерции – величины всегда положительные, так как координаты произвольной площадки входят в формулы в квадрате.
При повороте осей сумма осевых моментов инерции не изменяется.
Jx1+Jy1=Jx+Jy
Полярный момент инерции относительно точки равен сумме осевых моментов инерции относительно двух взаимно перпендикулярных осей, проходящих через эту точку: Jp=Jx+Jy
Момент инерции составного сечения равен сумме моментов инерции элементов этого сечения.