шпоры мехмат / 5.2 Определение напряжений при совместном действии изгиба и растяжения (сжатия)

5.2 определения напряжений при совместной действии изгиба и растяжения (сжатия)

В инженерной практике часто имеют место случаи одновременного действия на стержень поперечных и продольных нагрузок, причем последние могут быть приложены внецентренно. Такой случай показан на рис. 11.26. При этом внутренние усилия в заделке равны:

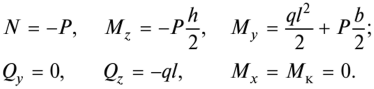
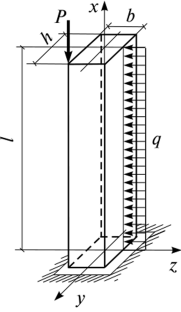
Рис. 11.26

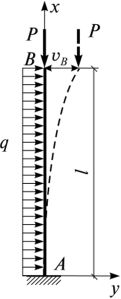
Рис. 11.27

В общем случае растяжения или сжатия с изгибом внутренние усилия определяются раздельно от действия всех составляющих нагрузок. Нормальные напряжения в поперечных сечениях определяются по общей формуле

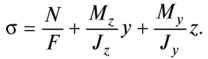
Приравняв это выражение нулю, получим уравнение нулевой линии

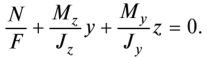
Положив в этом уравнении последовательно у = 0 и z = О, получим формулы для определения отрезков, отсекаемых нулевой линией на осях координат:

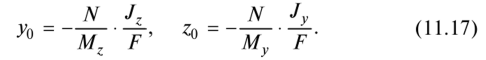
Как и во всех рассмотренных выше случаях сложного сопротивления, наибольшие растягивающие и сжимающие напряжения действуют в точках сечения, наиболее удаленных от нулевой линии. Для сечений типа прямоугольника и двутавра это противоположные угловые точки сечения. Значения наибольших и наименьших напряжений в угловых точках можно определить по формулам:

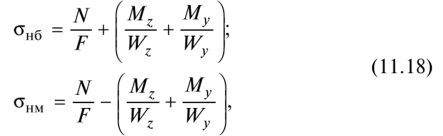
где величины изгибающих моментов M_z и М_у надо взять по абсолютной величине.

Напомним, что во всех предыдущих решениях использовался принцип независимости действия сил, позволяющий определять внутренние усилия для недеформированного состояния стержня. Строго говоря, это возможно только при малых деформациях. В противном случае принцип независимости действия сил использовать нельзя.

Рассмотрим, например, консольный стержень в условиях сжатия с изгибом (рис. 11.27). Если стержень обладает значительной гибкостью и прогибы от поперечной нагрузки достаточно велики, то сила Р вызывает дополнительный изгиб, а изгибающий момент в заделке от ее действия равен М = Pv_B. Для негибких стержней этот момент незначителен и его можно не учитывать. Для гибких стержней необходимо проводить расчет по так называемой деформированной схеме с учетом влияния продольных сил на изгиб.

---------------------------------------------------------------------------------------------------------------------------------------------------

2 вариант ответа на этот вопрос, по мне если есть время то можно прочитать и его но я выбрал бы первый ( 2 сыроват и мало инфы)

---------------------------------------------------------------------------------------------------------------------------------------------------

На основании принципа независимости действия сил нормальное напряжение в любой точке поперечного сечения стержня можно определить как алгебраическую сумму трех напряжений: от изгиба в двух взаимно перпендикулярных плоскостях и от действия продольной силы, т.е.

Подставляя в (11.10) значение напряжений из (5.4) и (10.23), получим

Каждое из слагаемых должно быть подставлено в (11.11) со своим знаком, определяемым но соответствующим эпюрам нормальных напряжений или, что то же самое, по характеру деформации бруса.

В случае плоского изгиба формула (11.11) принимает вид

Условие прочности проверяется для наиболее напряженной точки сечения из известного соотношения

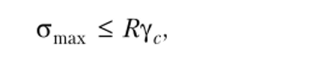
которое для общего случая принимает вид

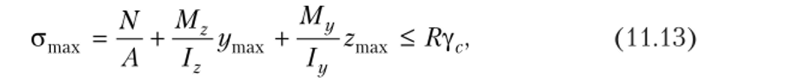
а для случая плоского изгиба