шпоры мехмат / 20.2 Порядок расчёта рамных конструкций методом сил

1. После подсчёта по формуле (16.1) числа лишних неизвестных в раме выберем основную систему (о.с.), изобразим и обозначим лишние неизвестные усилия.

2. Удовлетворяя требованиям кинематического соответствия основной и заданной систем, приравняем в них перемещения по направлению отброшенных связей (16.2).

3. Используя принцип независимости действия сил, составим уравнения совместности деформаций — канонические уравнения метода сил (16.4). Построим эпюры изгибающих моментов для всех единичных и грузового состояний.

Коэффициенты канонических уравнений определим по формуле

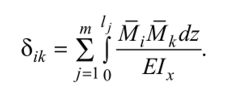
Если i - к, то эти коэффициенты называют главными, у них повторяющиеся индексы б,, (8ц, 8₂2, 833, ...). Коэффициенты 8„ всегда положительные, они не бывают нулями. Если i ^ к, то такие коэффициенты называют побочными (в отличие от главных, стоящих на главной диагонали системы канонических уравнений (16.4)). 8,* > О, 8,д < 0, 8,а = 0. На основании теоремы Максвелла 8,а = 8а,.

Грузовые перемещения находим по формуле Мора (15.32):

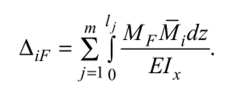
Для вычисления коэффициентов и свободных членов канонических уравнений используем правило Верещагина (15.33), формулу Симпсона (15.35) или формулу для перемножения трапеций (15.36). Найденные единичные и грузовые перемещения проверим (об этом подробнее речь пойдет позже).

4. Найдём лишние неизвестные, решив систему канонических уравнений известными для системы линейных алгебраических уравнений методами: методом последовательного исключения неизвестных, с помощью сокращенного алгоритма Гаусса, используя определители или компьютерные подпрограммы. Найденные неизвестные проверим подстановкой их в исходные канонические уравнения.

5. Используя принцип независимости действия, построим окончательную эпюру изгибающих моментов для заданной рамы (рис. 16.6, а), определив её ординаты по формуле: 

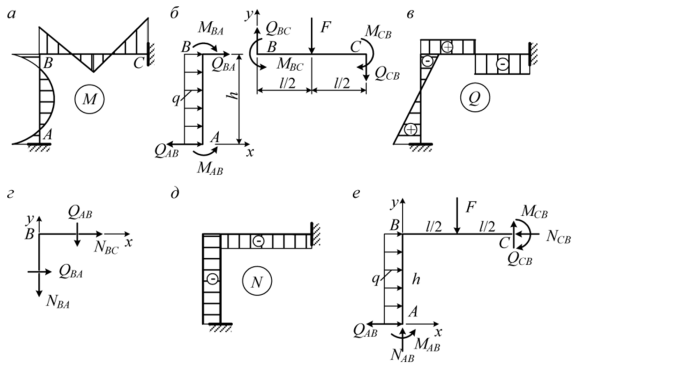
Обозначив узлы рамы А, В, С, разделим раму на отдельные стержни АВ, ВС, загруженные внешними нагрузками, концевыми изгибающими моментами, взятыми из эпюры М (она построена на растянутых волокнах), и концевыми поперечными силами, предполагая их положительными (рис. 16.6, б). Из условий равновесия ИтотВ = 0, ИтотА = 0 для стержня АВ находим Q_Ab и Qba- Записав уравнение Snpjc = 0, проверим результаты. Из условий равновесия ЕтотС = 0, ИтотВ = 0 для стержня ВС находим Q_Bc и Qcb- Записав уравнение Епр.у = 0, проверим и эти результаты. Затем построим эпюру Q для заданной рамы (рис. 16.6, в).

Вырежем жёсткий свободный узел В и загрузим его внешними сосредоточенными силами (в рассматриваемом случае их нет), концевыми поперечными силами, взятыми из эпюры Q, с учётом их знаков и концевыми продольными силами, предполагая их положительными (рис. 16.6, г). Из условий равновесия: Dnpj: = 0, Хпр.у = О находим Nbc и Nba- Построим эпюру N для заданной рамы (рис. 16.6, д).

Выполним статические проверки рамы «в целом», для чего раму (рис. 16.6, ё) отделим от опор, загрузим внешними нагрузками и реакциями, взятыми из эпюр (рис. 16.6, а, в, д). Должны выполняться следующие уравнения: ?пр.х = 0, Dnp.y = 0, ЕтотЛ - 0. Кроме того, должны выполниться кинематические проверки (они будут описаны позже).

Начиная расчёт рамы по методу сил, необходимо задать соотношения жёсткостей элементов рамы, а в ряде случаев — и сами жёсткости. После раскрытия статической неопределимости рамы и определения внутренних усилий в ней проверяют прочность элементов рамы и при недостаточной или избыточной прочности уточняют соотношения жёсткостей элементов рамы и повторяют расчёт. Таким образом, расчёт оказывается многоцикловым. В учебных целях ограничиваются одним расчётом (циклом).