шпоры мехмат / 17.1 Внут. силов. факторы при изгибе. Опред. изгиб. момента и поперечн. силы в сечен. и постр. эпюр. Контроль правильн. постр. эпюр
.docxПри плоском поперечном изгибе в балке возникают два вида внутренних усилий (рис.6.1,в): поперечная сила Qy , где y – ось симметрии (главная центральная ось) и изгибающий момент Mx. , где x – другая главная центральная ось сечения, нормальная к оси симметрии. В раме при плоском поперечном изгибе возникают три усилия: продольная N, поперечная Q силы и изгибающий момент M.

Для их определения используют метод сечений. Поперечная сила Q в сечении балки равна алгебраической сумме проекций на плоскость сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения.
Правило знаков для поперечных сил Q:

Изгибающий момент М в сечении балки равен алгебраической сумме моментов относительно центра тяжести этого сечения всех внешних сил, действующих по одну сторону от рассматриваемого сечения.
Правило знаков для изгибающих моментов M:

Метод сечений (см. рис. 2) состоит в том, что брус, находящийся в равновесии под действием системы внешних сил, мысленно рассекают на две части (рис. 2, а), и рассматривают равновесие одной из них, заменяя действие отброшенной части бруса системой внутренних сил, распределенных по сечению (рис. 2, б). Заметим, что внутренние силы для бруса в целом, становятся внешними для одной из его частей. Причем во всех случаях внутренние усилия уравновешивают внешние силы, действующие на отсеченную часть бруса.

В соответствии с правилом параллельного переноса сил статики приведем все распределенные внутренние силы к центру тяжести сечения. В результате получим их главный вектор R и главный момент M системы внутренних сил (рис. 2, в). Выбрав систему координат Oxyz так, чтобы ось z являлась продольной осью бруса и проецируя главный вектор R и главный момент M внутренних сил на оси, получим шесть внутренних силовых факторов в сечении бруса: продольную силу N, поперечные силы Qx и Qy, изгибающие моменты Мx и My, а также крутящий момент Т. По виду внутренних силовых факторов можно определить характер нагружения бруса. Если в поперечных сечениях бруса возникает только продольная сила N, а другие силовые факторы отсутствуют, то имеет место «растяжение» или «сжатие» бруса (в зависимости от направления силы N). Если в сечениях действуют только поперечная сила Qx или Qy - это случай «чистого сдвига». При «кручении» в сечениях бруса действуют только крутящие моменты Т. При «чистом изгибе» - только изгибающие моменты М. Возможны также комбинированные виды нагружения (изгиб с растяжением, кручение с изгибом и др.) – это случаи «сложного сопротивления». Для наглядного представления характера изменения внутренних силовых факторов вдоль оси бруса строят их графики, называемые эпюрами. Эпюры позволяют определить наиболее нагруженные участки бруса и установить опасные сечения.
Если говорить в общем, то метод сечений
мы всегда применяли на практике или
ргр. Тип проводим сечения между
действующими силами и ищем Q(как
сумму всех сил) и M(как
сумму моментов) на том z,
который мы отсекли (например z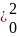 )
)
Построение эпюр производится под графиком условия в соответствии с произвольным масштабом, но равным для Q и М
Контроль правильности построения эпюр Q и M
Если поперечная сила положительная Q>0, то эпюра M имеет вниз сходящую линию (см. пример 1)
Если Q – отрицательная (Q<0), то эпюра М на этом участке имеет восходящую линию.
Если Q меняет знак с «+» на «-», то эпюра М меняет также направление (М имеет Мmax в этой точке)
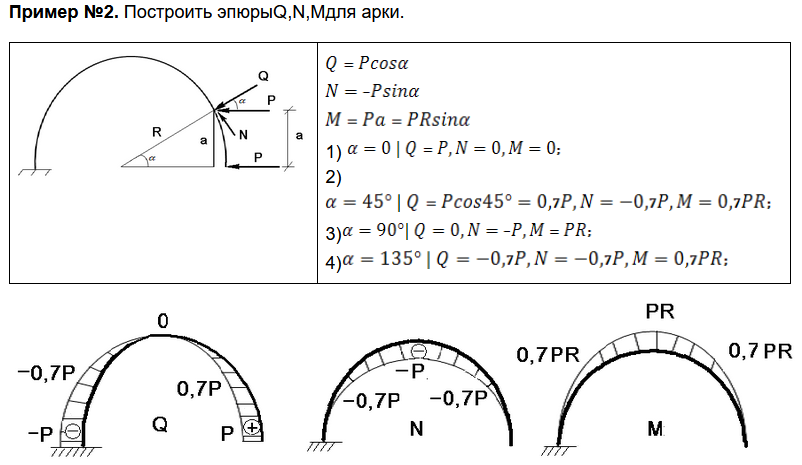
Если Q меняет знак с «-» на «+», то M имеет значение Mmin ( см. пример 2).
Под сосредоточенными силами на эпюре Q имеем скачок равный величине силы, а на эпюре М – перелом.
Под моментом на эпюре М имеем скачок на величину момента.
На участках нагруженных равномерно распределенной нагрузкой на эпюре Q имеем прямую наклонную линию, а на эпюре М – параболическую кривую ( см. пример 2) выгнутую в сторону действия нагрузки q.
На участках нагруженных неравномерно распределенной нагрузкой эпюры Q и М очерчены кривыми линиями.
.