Лекции по ТПС

Возможен и иной подход к решению задачи оценки погрешности разложения в ряд Котельникова непрерывных сигналов, спектр которых не является финитным. Практически интересной является ситуация, когда такой сигнал представляется в виде ряда (7.25), где в качестве полосы частот F фигурирует некоторая произвольно определяемая величина. При этом коэффициентами ряда являются не величины s1(k/2F) (7.26), а выборочные значения исходного сигнала , т.е. возникает необходимость оценки погрешности представления этого сигнала функцией s2(t) вида:

(7.27)

Очевидно, что функции и s2(t) совпадают лишь в случае, когда спектр исходного сигнала является финитным и расположен в пределах полосы частот 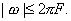В противном случае представление сигнала в форме (7.25) неизбежно приводит к погрешности, которая характеризуется величиной относительной среднеквадратической ошибки вида:

, (7.28)

где - спектр функции s2(t).

Спектр также является финитным и расположен, как спектр , в полосе частот Однако, в отличие от спектра , функция 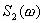в пределах этой полосы частот в общем случае не совпадает с функцией . Действительно, вычислим преобразование Фурье функции s2(t) в (1-62). Имеем

или

61

(7.29)

Заметим далее, что имеет место соотношение:

Тогда сумма под знаком интеграла может быть выражена:

так что (7.29) переписывается в виде:

(7.30)

Окончательно получаем:

62

Как показывают расчеты, в большинстве случаев, представляющих практический интерес, когда спектр в области 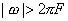убывает достаточно быстро, справедлива следующая оценка:

.

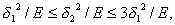ИСПОЛЬЗОВАНИЕ ТЕОРЕМЫ КОТЕЛЬНИКОВА ДЛЯ ПЕРЕДАЧИ СИГНАЛОВ ЖАТС

Разложение Котельникова было получено при предположении, что спектр функции ограничен частотой fв , т.е. функция имеет бесконечную длительность. Реальные сигналы имею бесконечную длительность и, следовательно, теоретически бесконечный спектр. Однако для них можно указать некоторую полосу частот, в которой сосредоточена основная мощность сигнала и которая содержит всю существенно необходимую информацию о сигнале. Разложение Котельникова для сигналов конечной длительности (финитных сигналов) будет иметь характер приближения соотношения

Таким образом, передачу непрерывных сигналов с ограниченной полосой частот можно свести к передаче N 2 fвT чисел – ее мгновенных значений в дискретных точках отсчета. Практически это может быть осуществлено следующим образом. На передающей стороне периодическая последовательность коротких импульсов модулируется по высоте (амплитуде) и поступает в канал. На приемном конце эта последовательность подается на идеальный (физически не-

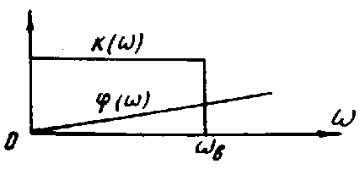
Рис. 7.4

Отклик такого фильтра на очень короткий импульс, дельта-функцию, определяется выражением

где t' – момент появления импульса на входе. Последовательность импульсов на входе' создает последовательность откликов на выходе с амплитудами, пропорциональными амплитудам импульсов на входе, т.е. обеспечивает воспроизведение модулирующего сигнала.

На практике для восстановления сигнала (АИМ) используются реальные фильтры нижних частот с граничной частотой fв . В этом случае для выделения модулирующего сигнала необходимо частоту следования импульсов

Теорема Котельникова лежит в основе всех видов импульсной модуляции и методов временного уплотнения каналов.

Теорема Котельникова позволяет также количественно подойти к оценке пропускной способности систем ЖАТС при заданных сигналах. Пусть, например, сообщение передается с помощью набора элементарных сигналов вида 'да' и 'нет'. Принимая за единицу пропускной способности канала число элементарных посылок за 1сек (эта единица называется ''бодом''), получим, что по каналу с полосой частот fв можно передавать не более 2 fв бод. Следовательно, в этом случае пропускная способность или, точнее, скорость передачи не может быть больше 2 бод на 1 Гц полосы частот.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. В чем заключается практическое применение теоремы Котельникова?

64

2.Какие виды погрешностей возникают при восстановлении сигнала рядом Котельникова?

3.Какой из видов погрешностей принципиально неустраним при восстановлении сигнала рядом Котельникова?

4.Каким должен быть выбран интервал дискретизации гармонического сигнала частотой F, чтобы восстановить его по взятым отсчетам?

5.Чему равна пропускная способность канала в бодах, наивысшая частота которого равна 3400 Гц, при передаче по нему информации импульсами постоянного тока положительной и отрицательной полярности?

ЛЕКЦИЯ 8. СИГНАЛЫ И ПОМЕХИ КАК СЛУЧАЙНЫЕ ПРОЦЕССЫ. РАСПРЕДЕЛЕНИЯ ВЕРОЯТНОСТЕЙ

Детерминированное, т.е. заранее известное сообщение не содержит информации, поэтому источник реальных сообщений следует рассматривать как устройство, которое осуществляет выбор из некоторого множества возможных сообщений. При этом конкретно реализованное сообщение выбирается из множества сообщений с определенной вероятностью.

Ансамбль - это множество на котором задана вероятностная мера. Ансамбли сообщений и сигналов могут быть конечны (в дискретном случае) или бесконечными.

Случайным (стохастическим) процессом X(t), или случайной функцией времени, называется множество W реализаций xr(t) с заданной на нем вероятностной мерой – плотностью распределения вероятностей, где индекс r определяет принадлежность реализации данному множеству.

Чтобы использовать эту возможность необходимо установить вполне определенное соответствие между каждой реализацией сообщения и каждой реализацией сигнала. Поскольку помехи также являются случайными процессами, постольку по реализации принятого сигнала можно лишь с некоторой вероятностью судить о том, какое именно сообщение было передано.

Случайный процесс X(t) считается полностью заданным, если для любого набора моментов времени t1, t2, ..., tn и любых значений сигнала x1, x2, ..., xn можно вычислить вероятность того, что в указанные моменты времени сигнал X(t) принимает значения не превышающие x1, x2,..., xn

F( x1, x2,..., xn; t1, t2,..., tn)=P{X(t1) x1, X(t2) x2, ..., X(tn) xn },

65

где P{X(t1) x1, X(t2) x2, ..., X(tn) x1}- совместная вероятность событий записанных в скобках.

X(tk) - случайная величина, так называемое, сечение случайного процесса в момент времени tk.

Функция F(x1, x2, ..., xn; t1, t2, ..., tn)- n-мерная функция распределения вероятностей (ФРВ) процесса. Ее аргументами являются x1, x2, ..., xn, а t1, t2,..., tn- играют роль параметров.

Если существуют частные производные функции распределения по всем xk, можно определить n-мерную плотность распределения вероятностей (ПРВ) путем дифференцирования ФРВ по всем аргументам

В частном случае одномерного распределения (n=1) получаем: w(x,t) 0 при всех значениях x ;

w(x,t)dx 1;

0 F(x,t) 1;

F( ,t) 1; F( ,t) 0;

x

w( ,t)d F(x,t).

Стационарный - это случайный процесс, у которого определенная группа вероятностных характеристик (математическое ожидание, дисперсия, плотность распределения вероятностей) не изменяется при сдвиге начала отсчета, т.е. при замене аргумента t на (t+ ), где произвольный интервал времени.

Различают стационарность в узком (строгом) и широком смыслах.

66

Процесс стационарен в узком смысле когда n-мерные распределения вероятностей не изменяются во времени (точнее не зависят от выбора момента начала отсчета), т.е., если говорить о ПРВ, то для любого n и справедливо

w(x1, x2 ,...,xn;t1,t 2 ,...,t n) w(x1, x2 ,...,xn;t1 ,t 2 ,...,t n ) Процесс назы-

вают стационарным в широком смысле, когда его среднее значение ( математическое ожидание) и дисперсия, вообще не зависят от времени, а корреляционная функция зависит лишь от t 2

Процесс стационарный в узком смысле стационарен и в широком, но не наоборот.

По виду закона распределения вероятностей случайные процессы делятся на две группы: гауссовские (нормальные) и негауссовские.

Нормальным называется процесс, у которого любая n-мерная ПРВ определяется в виде:

связанные между собой.

В одномерном случае для нестационарного процесса:

Для стационарного процесса формула упрощается:

Случайные процессы могут быть трех типов: совершенно случайные, марковские и немарковские.

Совершенно случайный процесс (белый шум)- процесс, последующие значения которого статистически не зависят от предыдущих. Такой процесс полностью определен одномерной ПРВ.

Марковский - процесс, у которого зависимость текущего значения от предыстории не распространяется далее непосредственно предшествующего мо-

67

мента. Такой процесс определяется одномерной начальной ПРВ и ПРВ перехода из состояния в состояние.

Немарковские - все остальные случайные процессы.

ЧИСЛОВЫЕ ХАРАКТЕРИСТИКИ СЛУЧАЙНЫХ СИГНАЛОВ (ПОМЕХ)

Среднее по ансамблю значение случайного процесса (математическое ожидание)

где M[ X (t)] символ операции определения математического ожидания.

Математическое ожидание - детерминированная функция времени. Разность между случайным процессом и его математическим ожиданием называют цен-

трированным процессом X X (t) X (t) ;

Значение m X (t) при каждом значении аргумента t равно математическому ожиданию значения случайной функции X(t) при данном t.

Дисперсия - случайного процесса (центральная моментная функция второго порядка) - математическое ожидание квадрата соответствующего центрированного процесса:

Дисперсия характеризует степень рассеяния возможных реализаций случайного процесса от его среднего значения, физический смысл которой - средняя мощность случайного процесса: сигнала или помехи.

Часто используют среднее квадратическое отклонение σХ(t), физический смысл которой – действующее значение напряжения:

σХ2(t) = D[X(t)].

Средний квадрат — это моментная функция второго порядка, математическое ожидание квадрата самого (не центрированного) случайного процесса.

У стационарных случайных процессов, как было отмечено выше ранее, m X (t) = тх, σХ2(t) = σХ2.

68

Если стационарный эргодический процесс является напряжением или током на нагрузке сопротивлением 1 Ом, средний квадрат является полной средней мощностью процесса, квадрат математического ожидания — мощностью постоянной составляющей, а дисперсия — среднюю мощностью переменной составляющей.

Важно для практики правило "Трех сигм": с той или иной вероятностью р можно утверждать, что значения непрерывного случайного процесса X(t) не выходят за пределы тх ± З σХ.. Согласно неравенству Чебышева, вероятность р не может быть меньше 8/9, а для нормального процесса р ~ 0,997.

Кроме среднего значения по ансамблю, можно определить среднее значение случайного процесса по времени - постоянную составляющую реализации.

Постоянные составляющие от времени не зависят, но являются случайными величинами, поскольку их значения зависят от реализации сигнала.

Стационарный процесс называют эргодическим, если для него усреднение по времени по одной достаточно продолжительной реализации приводит к тому же результату, что и статистическое усреднение, т. е. постоянная составляющая равна математическому ожиданию, мощность переменной составляющей равна дисперсии и т. п.

Стационарность — необходимое, но не достаточное условие эргодичности. Эргодичность требует того, чтобы результаты усреднения по времени различных реализаций совпадали друг с другом и с результатом усреднения по множеству.

Эргодичность заключается в том, что реализации процесса "похожи" друг на друга.

Эргодичность существенно упрощает определение распределений вероятностей и числовых характеристик, поскольку они могут быть определены по одной реализации (не надо производить усреднение по множеству), например, определение одномерной интегральной функции сводится к измерению относительного времени пребывания реализации х(t) ниже заданного уровня анализа.

ПРИМЕРЫ РАСПРЕДЕЛЕНИЙ ВЕРОЯТНОСТЕЙ СИГНАЛОВ И ПОМЕХ В СИСТЕМАХ ЖАТС

Флуктуации фазы полезного сигнала в системах контроля состояний рельсовых линий (КРЛ) с когерентными приемниками в летний период являются нормальными стационарными процессами со средним значением 73,6о и средним квад-

69

ратическим значением 0,83°. В осенний период для флуктуации фазы может быть использовано ПРВ Вейбулла с параметрами α = 31,11 и β = 75,84.

Распределение максимальных значений выбросов помех при электротяге постоянного тока подчиняется гамма-распределению с параметрами α = 16,31 и

β = 4,12.

ПРВ длительности импульсных помех в каналах КРЛ с частотами настройки 25 и 175 Гц также хорошо аппроксимируется гамма-распределением, а ПРВ интервала в потоке помех — логарифмическая нормальная (при 25 Гц) и экспоненциальная (при 75 Гц).

При исследовании радиолокационных измерителей параметров движения отцепов на сортировочных горках для ПРВ сигналов, отраженных от движущихся отцепов, используют распределения Накагами и Вейбулла, а для ПРВ выбросов их огибающих — логарифмически нормальный закон. ПРВ амплитуды огибающей отраженного сигнала описывается распределением Накагами.

При исследовании сетей железнодорожной технологической радиосвязи метрового диапазона выявлено, что пространственные флуктуации напряженности поля характеризуются распределением вероятностей амплитуд основных поляризационных компонентов, подчиняющихся закону Рэлея—Райса, а ПРВ результирующей амплитуды напряженности электрического поля вторичного излучения описывается законом Рэлея.

Для анализа систем железнодорожной связи большое значение имеет правильный выбор модели речевого сообщения.

Наиболее хорошо зарекомендовала себя при анализе русскоязычных речевых сообщений аппроксимация ПРВ

W(x) R e- x e- x .

При использовании реализации сообщения устной речи продолжительностью 1 час, с частотой дискретизации 44100 Гц и разрешением 16 бит (динамический диапазон разбивался на 216=65536 уровней) уточнены значения коэффициентов:

R=3,396/σх; β=102,845/σх; α=7,272/σх.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1. Какой процесс (сигнал или помеха) называется случайным?

70