Лекции по ТПС

Характеристики корректора выбираются такими, чтобы в полосе частот входного сигнала выполнялись условия (рис. 6.4):

Необходимым условием коррекции линейных искажений является неравенство нулю амплитудно-частотной характеристики корректируемого четырехполюсника в области корректируемых частот.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Что понимается под импульсной характеристикой системы с постоянными параметрами?

2.Какая система является линейной?

3.Как связаны между собой импульсная характеристика и передаточная функция линейной системы?

4.Какие причины вызывают нелинейные искажения сигналов?

5.Каким требованиям должна удовлетворять передаточная функция четырехполюсника системы передачи, что он не вносил нелинейных искажений сигнала?

ЛЕКЦИЯ 7. ПРЕДСТАВЛЕНИЕ ДЕТЕРМИНИРОВАННОГО СИГНАЛА РЯДОМ КОТЕЛЬНИКОВА

Реальные сигналы имеют ограниченную полосу частот. Такие сигналы обладают замечательным свойством, впервые уставленным В. А. Котельниковым и выраженным в его теореме, играющей фундаментальную роль в теории и технике передачи сигналов.

Если в общем случае непрерывная функция времени определяется на конечном интервале бесчисленным множеством своих мгновенных значений (рис.7.1), то функции времени с ограниченным спектром согласно теореме Котельникова на конечном интервале определяются конечным множеством своих значений.

51

Рис.7.1

Отсутствие в функции частот выше некоторой граничной накладывает определенные ограничения на ее изменение в достаточно малом интервале времени t . Поэтому через точки, изображающие мгновенные значения функции и взятые через определенный интервал времени друг от друга, можно провести кривую одним единственным способом.

Теорему В. А. Котельникова можно сформулировать в следующем виде:

Любой сигнал f(t), спектральная плотность которого отлична от нуля в полосе частот 0 fв , можно точно восстановить (интерполировать) по ее отсчетам

Функциями разложения в ряде Котельникова являются так называемые функции отсчетов

Таким образом, в момент времени t k t сумма ряда (7.1) определяется лишь k-ым слагаемым, все остальные члены ряда в этот момент времени обра-

52

щаются в нуль. Разложение функции в ряд Котельникова иллюстрируется на рис.7.2.

Рис.7.2

Функции отсчета ортогональны на бесконечном интервале времени, т.е.

53

отлична от нуля в полосе частот 0 в . Тогда для этой функции обратным преобразованием Фурье получим

Подставляя (7.11) в (7.7) и меняя порядок суммирования и интегрирования, получим

54

функция вне рассматриваемого интервала [-T/2,T/2] удовлетворяет соотношению

при 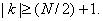(7.15)

Заметим, что из этого условия вовсе не следует тождественное равенство нулю функции во всех точках области | t |>T/2, так как это противоречило бы условию финитности спектра .

В общем случае, условие (7.15) не выполняется, так что имеет место отличная от нуля погрешность аппроксимации. Введем функцию вида:

характеризующую рассматриваемую погрешность. Из (7.15) имеем:

.

Тогда ошибка аппроксимации (7.15) на бесконечном интервале времени с учетом условия ортогональности функций определяется выражением:

(7.16)

Очевидно, что величина зависит от проведения функции в области | t |>T/2 и может достигать больших значений, если функция не убывает достаточно быстро при Положим, что можно определить некоторый интервал [-T0/2,T0/2] так, чтобы существовало целое положительное число m, для которого

. (7.17)

Таким образом, при достаточно больших m можно считать, что в интервале [-T0/2,T0/2] сосредоточена основная часть энергии сигнала .

При имеем:

(7.18)

56

Относительная среднеквадратическая ошибка аппроксимации (7.15), равная отношению величины к полной энергии E сигнала , может быть оценена с учетом очевидного неравенства:

откуда

(7.19)

С целью оценки порядка величины /E c учетом (1-51) положим

(7.20)

Тогда окончательно получаем:

(7.21)

Таким образом, выбирая величину T можно с заданной точностью (в смысле величины /E) передать сигнал с помощью конечного числа отсчетных значений N=2FT. При этом следует отметить, что на практике обычно приходится иметь дело с сигналами , основная часть энергии которых сосредоточена на конечном интервале времени, так что определение величины m не вызывает затруднений.

Оцененная ошибка определяется погрешностью аппроксимации (7.21) как на интервале [-T/2, T/2], так и вне этого интервала. Представляет интерес оценка степени отличия функции и внутри интервала [-T/2, T/2], т.е. в конечном счете, оценка ошибок, имеющих место при передаче представляющей наибольший, в том или ином смысле, интерес части исходного непрерывного сигнала , имеющего бесконечную длительность. С этой целью произведем оценку величины используя неравенство Коши:

Замечая, что при целых k

57

получаем:

Для значений t в интервале [-T/2, T/2] имеем:

откуда

(7.22)

Относительная ошибка аппроксимации в интервале [-T/2, T/2] может быть оценена следующим образом:

(7.23)

Вид функции для двух значений и приведен на рис. 7.3 а, б.

58

Рис.7.3

Здесь же пунктиром показана зависимость

от безразмерного параметра t/T. Как видно из рис. 7.1, погрешность аппроксимации на значительной части рассматриваемого интервала [-T/2, T/2] не пре-

вышает величины 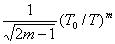при любых значениях интервала дискретизации

, а в моменты дискретизации, как и следовало ожидать, равняется нулю. При этом оценка погрешности аппроксимации увеличивается по мере приближения к краям рассматриваемого интервала, что также вполне естественно, поскольку влияние отброшенных членов ряда наиболее сильно сказывается именно в областях интервала [-T/2, T/2], близких к моментам дискретизации, соответствующим максимальным значениям отброшенных членов ряда.

Вообще говоря, с уменьшением интервала дискретизации при фиксированном значении t ошибка аппроксимации должна уменьшаться, поскольку при этом уменьшается влияние отброшенных членов ряда, максимальные значения которых соответствуют моментам дискретизации вне интервала [-T/2, T/2]. То обстоятельство, что максимальные значения оценки в промежутках между моментами дискретизации остаются практически постоянными при уменьшении для фиксированных значений t на значительной части интервала [-T/2, T/2] и увеличиваются для значений t вблизи границ этого интервала (см. рис. 7.1), указывает на несовершенство полученной оценки. Однако при достаточно больших значениях m и T>T0 оценка (7.21) оказывается вполне удовлетворительной.

Погрешность, вызванная ограничением ширины спектра сигнала

59

Перейдем теперь к рассмотрению погрешностей, обусловленных тем, что спектр реальных сигналов не является финитным. Одним из возможных подходов к решению этой задачи является следующий. Выделим некоторую полосу частот в пределах которой сосредоточена наиболее существенная (в том или ином смысле) часть энергии сигнала , и введем в рассмотрение сигнал s1(t) с финитным спектром S1( ) вида

(7.24)

Сигнал s1(t) может быть разложен в ряд Котельникова в форме:

(7.25)

причем коэффициенты ряда (7.25) выражаются в виде:

(7.26)

Относительная среднеквадратическая погрешность представления исходного сигнала функцией s1(t) (7.25) равна:

(7.27)

При соответствующем выборе величины F ошибка (7.27) может быть сделана сколь угодно малой, если спектр убывает по модулю при стремлении к бесконечности.

60