Лекции по ТПС

янию Хэмминга соответствует не самое большое расстояние Евклида , и т.д.

Таблица 38.1. Соответствие расстояний Хэмминга и Евклида для сигналов ФМн-8

Таким образом, поскольку манипуляционный код Грея для сложных сигналов не обеспечивает оптимального согласования кодека и модема, необходимо

найти методы дальнейшего повышения свободного евклидова расстояния и, соответственно, энергетической эффективности .

СОГЛАСОВАНИЕ НА ОСНОВЕ РАЗБИЕНИЯ АНСАМБЛЯ НА ВЛОЖЕННЫЕ ПОДАНСАМБЛИ

В начале 80 х гг. Унгербоек (Ungerboeck G.) опубликовал статью, в которой, анализируя СКК на базе ансамбля ФМн-8 и сверточного кода со скоро-

стью , сформулировал ряд правил построения СКК. Поэтому СКК построенные по этим правилам (Trellis-Coded Modulation – ТСМ), часто называют СКК Унгербоека.

По способу согласования модуляции и кодирования СКК Унгербоека относятся к конструкциям, полученным на основе разбиения ансамбля сигналов на вложенные подансамбли. Разбиение осуществляется таким образом, что подан-

самбли содержат равное количество сигналов, расстояния между соседними

сигналами подансамблей одинаковы, минимальные расстояния 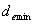между сигналами подансамблей увеличиваются с каждым шагом разбиения; при этом левая ветвь разбиения кодируется символом «0», а правая «1». Считывание кодовой комбинации, соответствующей сигнальной точке на амплитудно-фазовой плоскости, осуществляется снизу вверх. Разбиение для ансамбля сигналов ФМн- 8 представлено на рис. 38.4.

Как следует из рис. 38.4, исходный ансамбль разбивается на подансамбли

данном примере три этапа, заключающихся в разбиении каждого из подансамблей предыдущего этапа на 2 равноэлементных подансамбля.

Рис.38.4

В общем случае количество этапов полного разбиения ансамбля из сигналов на вложенные подансамбли определяется выражением:

т. е. совпадает с кратностью ансамбля .

В ансамбле из сигналов кратности каждой сигнальной точке соответствует блок двоичных символов . Соответствие между кодовым блоком и сигнальной точкой на плоскости определяет манипуляционный код.

Достижение наибольшей помехоустойчивости непосредственно связано с увеличением евклидова расстояния между передаваемыми сигнальными последовательностями. Решетчатая диаграмма сверточного кода, ребра которой промаркированы сигнальными точками, полностью отображает весь набор разрешенных сигнальных последовательностей. Таким образом, величина свободного

евклидова расстояния зависит от маркировки ребер решетчатой диаграммы сигнальными точками (канальными символами).

Унгербоек на примере ансамбля сигналов ФМн-8 сформулировал четыре необходимых правила маркировки ребер сигнальными точками:

–все сигнальные точки используемого ансамбля сигналов должны встречаться с одинаковой частотой и с определенной степенью регулярности и симметричности;

312

–переходы из одного и того же состояния соответствуют сигналам из подансамблей В0 или В1;

–переходы в одно и то же состояние соответствуют сигналам из подансамблей В0 или В1;

–параллельные переходы между состояниями соответствуют сигналам из подансамблей С0 или С1, или С2, или С3.

Как показывает анализ, СКК Унгербоека имеют несколько более высокие частотно энергетические характеристики по сравнению с традиционными СКК, при той же сложности реализации. Это определило их бурное внедрение в технике связи. Но известные правила построения СКК Унгербоека, хотя и снижают размерность переборной задачи синтеза, но не обеспечивают гарантированное построение СКК с максимальными частотно-энергетическими характеристиками. В то же время, основной целью работ в области синтеза систем сигналов и СКК является поиск таких способов их формирования и обработки, которые при заданных ограничениях на сложность устройств формирования и приема, временные задержки, позволяли бы приблизиться к известной шенноновской границе.

При построении многомерных СКК возникает проблема выбора манипуляционного кода, поскольку известные методы его построения (правила построения кодов Грея и разбиения ансамбля на вложенные подансамбли Унгербоека) не всегда позволяют согласовать евклидовы и хэмминговы расстояния. Именно с этим связаны многие проблемы построения многомерных СКК.

Синтез многопозиционных ансамблей сигналов и СКК, построенных на их основе, является одним из направлений решения более общей задачи статистического согласования вероятностных характеристик передаваемого информационного сигнала и вероятностных характеристик канала. В рамках этих традиционных задач, такое согласование осуществляется на уровне канальных символов или их блоков (супербукв канала). При этом подходы к построению алфавита таких супербукв (ансамблей сигналов и СКК) могут существенно отличаться между собой, но направлены на решение этой общей проблемы.

Известно, что ансамбль сигналов, соответствующий полному двоичному коду длины в пространстве соответствующей размерности , построенный заменой «1» на «–1», а «0» на «+1», соответственно, обладает практически идеальным манипуляционным кодом. Минимальным хэмминговым расстояниям таких ансамблей соответствуют ребра -мерного куба, которые характеризуются и минимальными евклидовыми расстояниями.

313

Кодовые комбинации и соответствующие им координаты сигнальных векторов приведены в табл. 38.2; графическое изображение ансамбля представлено на рис. 38.5.

При приеме сигналов такого ансамбля минимальная ошибка (ошибочный прием одной координаты сигнальной точки) приводит к неправильному приему одного бита информации. Ошибочный прием двух координат сигнальной точки приводит к искажению двух бит информации и так далее. Однако, если рассмот-

реть зависимость между хэмминговыми и евклидовыми расстояниями для такого ансамбля, то можно выявить следующую закономерность, связывающую эти две величины:

где – радиус сферы.

Таблица 38.2. Взаимосвязь кодовых комбинаций манипуляционного кода и координат сигнальных векторов

Таким образом, взаимосвязь между евклидовыми и хэмминговыми расстояниями в многомерном ансамбле сигналов нелинейная, хотя большему хэмминговому расстоянию будет соответствовать большее евклидово расстояние.

Если мощность и энергия сигналов являются постоянными величинами, не зависящими от номера, то ансамбли таких сигналов считают сигналами поверх- ностно-сферической упаковки.

314

Рис.38.5

В противном случае ансамбли сигналов рассматривают как объемные упаковки. Сохранение манипуляционного кода, принятого для простого трехмерного куба, в значительной мере сохраняет пропорциональность между евклидовыми и хэмминговыми расстояниями и поэтому будет наилучшим и для наиболее плотного ансамбля. Для других комбинаций манипуляционных кодов для сигнальных векторов изначально не будет соблюдаться взаимная пропорциональность между евклидовыми и хэмминговыми расстояниями.

Таким образом, практически невозможно создать идеальный манипуляционный код и, следовательно, целесообразно строить манипуляционные коды, у которых хотя бы частично выполняется взаимосвязь между евклидовыми и хэмминговыми расстояниями.

КОНТРОЛЬНЫЕ ВОПРОСЫ

1.Что называют эффективностью систем ЖАТС и как она определяется количественно?

2.Как можно осуществить обмен эффективности между и ?

3. Как изменится энергетическая эффективность системы передачи дискретных сообщений при уменьшении требуемой вероятности ошибки? Уменьшится она или увеличится? Покажите это на примере двоичного канала.

4. Какой общий вывод о связи между помехоустойчивостью и эффективностью можно сделать для систем с ФМн, ЧМн и АМн двоичными сигналами?

5. На какой основе могут быть построены системы передачи, в которых достигается повышение как энергетической, так и частотной эффективности?

315

ЛИТЕРАТУРА:

Перечень основной учебной литературы

1.Горелов Г.В., Фомин А.Ф., Волков А.А., Котов В.К. Теория передачи сигналов на железнодорожном транспорте. – М., Транспорт, 1999 – 415с. и электронный ресурс: Теория передачи сигналов на железнодорожном транспорте. / учеб. для вузов ж.-д. трансп. - Электрон. дан. — М.: УМЦ ЖДТ, 2013. — 532 с.

— Режим доступа: http://e.lanbook.com/book/58968.

2.Котов В.К., Останькович О.Д., Сидорович Д.Ю. Математические методы обработки сигналов в системах железнодорожной автоматики и связи. // Учебное пособие по курсу ТПС. – СПб.: ПГУПС, 2013. – 53 с.

3.Котов В.К. Определение параметров сигналов и устройств системы передачи информации. // Учебное пособие к курсовому проектированию. – СПб.: ПГУПС, 2020. – 64с.

Перечень дополнительной учебной литературы

1.Мощенский Ю.В. Теоретические основы радиотехники. Сигналы. [Электронный ресурс]: учеб. пособие / Ю.В. Мощенский, А.С. Нечаев. — Электрон. дан. — СПб.: Лань, 2016. — 216 с. — Режим доступа: http://e.lanbook.com/book/87585.

2.Лебедько Е.Г. Теоретические основы передачи информации. [Электронный ресурс]: моногр. — Электрон. дан. — СПб.: Лань, 2011. — 352 с. — Режим до-

ступа: http://e.lanbook.com/book/1543.

3.Магазинникова А.Л. Основы цифровой обработки сигналов. [Электронный ресурс]: учеб. пособие — Электрон. дан. — СПб.: Лань, 2016. — 132 с. — Режим доступа: http://e.lanbook.com/book/76274.

316