Лекции по ТПС

Тогда информационная эффективность для гауссовского непрерывного канала может быть найдена по формуле:

(36.7)

.

Согласно теореме Шеннона, при соответствующих способах передачи и приема величина может быть сколь угодно близкой к единице. При получаем предельную зависимость между и :

Наглядно данная зависимость представляется в виде кривой на плоскости (рис. 36.1). Эта зависимость, часто называется границей (пределом) Шеннона: она отражает наилучший обмен между и в непрерывном канале. Анализ соотношения (36.6) и предела Шеннона показывает, что повышение частотной

эффективности (т.е. снижение затрат полосы ) требует увеличения энергетических затрат (снижения энергетической эффективности).

291

Рис.36.1

Для непрерывного канала частотная эффективность изменяется в пределах от 0 до ∞, в то время как энергетическая эффективность ограничена сверху:

.

Аналогичные предельные зависимости можно получить и для других моделей канала, если в (36.2) и (36.3) вместо скорости подставить выражение для пропускной способности соответствующего канала. Предельные зависимости - номограммы позволяют определить системы, удовлетворяющие заданным требованиям по энергетической и частотной эффективности, и установить, насколько эти показателя близки к предельным.

ЭФФЕКТИВНОСТЬ АНАЛОГОВЫХ И ЦИФРОВЫХ СИСТЕМ ПЕРЕДАЧИ ИНФОРМАЦИИ

В системах передачи дискретных сообщений сигнал формируется с помощью кодирования и модуляции. При этом кодирование осуществляется обычно в два этапа: кодирование источника с целью сокращения его избыточности и кодирование канала с целью уменьшения вероятности ошибки за счет введения избыточности кода. При этом выражение (36.1) для информационной эффективности системы передачи дискретных сообщений можно представить в виде произведения:

292

канала; – эффективность модема, зависящая от вида модуляции и способа обработки сигнала в канале.

Средняя скорость передачи информации в системе при использовании мно-

где – скорость помехоустойчивого кода. Тогда энергетическая эффективность

(36.10)

,

частотная эффективность может быть найдена по формуле

(36.11)

,

где – энергия сигнала; – энергия, затрачиваемая на передачу одного бита информации.

Значения можно определить по известным формулам или графи-

кам, рассчитанным для вероятности ошибки .

На рис. 36.1 приведены предельные кривые 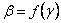для симметричных двоичных дискретных и дискретно-непрерывных каналов (ДНК). При этом выходом ДНК считается согласованный фильтр в оптимальной схеме приема дис-

кретных сообщений при примитивном кодировании ().

Для двухпозиционных систем 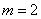предельное значение полосы пропускания канала равно частоте манипуляции. В этом случае частотная эффективность

В двоичных симметричных каналах с различными видами модуляции максимум

энергетической эффективности достигается при , при этом удельная скорость передачи стремится к нулю. Предельные значения показателей эффективности достигаются при R=C и при малой вероятности ошибки. Для определения β и γ могут использоваться приближенные формулы:

где – размерность сигнала, в -позиционной системе. В табл.36.1 приведены значения m и формулы для приближенных расчетов γ некоторых ансамблей сигналов.

Таблица 36.1. Формулы для приближенных расчетов частотной эффективности некоторых ансамблей сигналов

Ансамбль

сигналов

Вреальных системах вероятность ошибки всегда имеет ненулевое значение

и. В этих случаях при заданном значении можно определить отдельно и и построить кривые .

Вкоординатах и каждому варианту реальной системы будет соответствовать точка на плоскости (рис.36.2). Все эти точки располагаются ниже предельной кривой Шеннона и ниже предельной кривой соответствующего канала. Ход этих кривых зависит от вида модуляции, метода кодирования и способа обработки сигналов. На рис. 36.2 указано число позиций дискретного сигнала . Кривые рассчитаны на основании формул оценки помехоустойчивости различ-

294

при вероятности ошибки на бит 1∙10-5. При этом занимаемая полоса частот для ЧМн , а для ФМн (АМн).

Анализ рис. 36.2 показывает, что в системах с ЧМн при увеличении числа позиций энергетическая эффективность увеличивается, а частотная эффективность уменьшается. В системах с ФМн и ОФМн, наоборот, с увеличением коэффициент уменьшается, а – увеличивается. Таким образом, условия обмена на за счет изменения числа позиций сигналов в системах связи с ЧМн и ФМн различны.

Представленные на рис. 36.2 результаты позволяют определить системы, удовлетворяющие заданным требованиям по энергетической и частотной эффективности, и установить, насколько эти показатели близки к предельным.

После выбора системы по показателям и , информационная эффективность вычисляется с использованием формулы (36.7).

Например, для сигналов АМн-2 показатель информационной эффективности составляет , а для ЧМн-2 ; для ФМн-2 , а для ФМн- 4 .

295

Рис.36.2

Анализ предельных кривых показывает, что эффективность дискретных систем передачи можно существенно повысить, если вместо двоичных применять многопозиционные сигналы ().

Эффективность передачи непрерывных сообщений в значительной степени зависит от вида модуляции. Для сравнительного анализа различных видов моду-

ляции обычно используют выигрыш по отношению сигнал/шум () и коэффициент использования пропускной способности каналов передачи информации ()

(36.13)

296

В табл. 36.2 приведены данные сравнительного анализа эффективности раз-

личных видов модуляции, полученные при дБ и пик-факторе для гауссовского канала при оптимальной обработке сигналов.

Таблица 36.2. Значения выигрыша и информационной эффективности некоторых систем передачи непрерывных сообщений

Анализ показывает, что наибольшая информационная эффективность достигается при однополосной модуляции, однако значение обобщенного выигрыша для этого вида модуляции () свидетельствует о том, что в системе отсутствует выигрыш по помехоустойчивости. Одноканальные системы ЧМ и ФИМ примерно равноценны. В этих системах, а также в цифровых системах с ИКМ, высокая помехоустойчивость может быть достигнута с помощью увеличения ширины спектра сигнала, т.е. за счет частотной избыточности. При больших индексах ФМ и ЧМ приближаются по помехоустойчивости к идеальной системе (выигрыш составляет десятки и сотни раз), но информационная эффективность таких систем мала (0,12 – 0,17) из-за большой частотной избыточности. Основными способами повышения эффективности передачи непрерывных сообщений являются устранение избыточности, статистическое уплотнение и применение цифровых видов модуляции.

297

Аналоговые системы ОМ, AM и узкополосная ЧМ обеспечивают высокую частотную эффективность при сравнительно низкой энергетической эффективности. Применение этих систем целесообразно в каналах с хорошей энергетикой

(при больших значениях ) или в тех случаях, когда требуемое значе-

ние мало. Цифровые системы обеспечивают высокую -эффективность при достаточно хорошей -эффективности. В каналах с ограниченной энергетикой

(при малых значениях ) преимущества цифровых систем особенно заметны.

При высоком качестве передачи, когда требуемые значения велики, широкополосная ЧМ и цифровые системы обеспечивают примерно одинаковую эффективность.

В многоканальных системах эффективность связи снижается за счет несовершенства системы разделения сигналов.

Расчеты показывают, что наиболее эффективным является метод временного разделения каналов; менее эффективен метод частотного разделения. При временном разделении пропускная способность не зависит от числа каналов, т.к. в каждый момент времени передается только один сигнал. При ЧРК пропускная способность канала с ограниченной средней мощностью сигнала также не зависит от числа каналов. При разделении по форме между n парциальными каналами делится только мощность, полоса частот и время передачи используются одновременно всеми сигналами. В этом случае информационная эффективность уменьшается с увеличением n, причем амплитудное ограничение сигнала слабо влияет на эту зависимость.

Показатели частотной, энергетической и информационной эффективности для систем с множественным доступом определяются на основании суммарной скорости передачи системы ЖАТС, зависящей от методов формирования и обработки информационных сигналов в парциальных каналах и методов доступа.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Какие критерии эффективности используются для оценки эффективности систем передачи информации?

2.Что характеризует предел Шеннона?

3.От чего зависит эффективность аналоговых систем передачи информации, при каком виде модуляции достигается наибольшая информационная эффективность?

298

4.Как можно повысить эффективность дискретных систем передачи информации?

5.За счет чего снижается эффективность в многоканальных системах передачи информации?

ЛЕКЦИЯ 37. ВЫБОР СИГНАЛОВ И ПОМЕХОУСТОЙЧИВЫХ КОДОВ

Эффективность систем передачи дискретных сообщений можно существенно повысить путем применения многопозиционных сигналов и помехоустойчивых (корректирующих) кодов.

Многопозиционные сигналы

Ансамбль сигналов , где , на отрезке можно представить:

(37.3)

(37.5)

,

коэффициент взаимной корреляции рассматриваемых сигналов.

На рис. 36.2 приведены -диаграммы для некоторых ансамблей многопозиционных сигналов. Центральное место на рис.36.2 занимают кривые для систем с сигналами ФМн-4, которые относятся к классу многопозиционных при 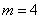. В цифровых сетях система ФМн-4 является наиболее распространенной и принята в качестве стандарта, поэтому при сравнительной оценке эффективности систем она принята за эталон. Если начало координат перенести в точку, соответствующую ФМн-4, то в новой системе координат по вертикальной оси будет отсчитываться энергетический выигрыш рассматриваемых систем по сравнению с ФМн-4, а по горизонтальной оси – выигрыш по удельной скорости. В этой системе координат все возможные системы связи можно условно разделить на четыре группы, соответствующие четырем квадрантам на плоскости.

Малоэффективные системы (III квадрант), имеющие относительно ФМн-4 проигрыш по 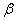и , например, АМн-2, ЧМн-2. Системы с высокой энергетической эффективностью (II квадрант), обеспечивающие выигрыш по и проигрыш по (системы с помехоустойчивыми кодами). Системы с высокой частотной эффективностью (IV квадрант), обеспечивающие выигрыш по и проигрыш по (системы с многопозиционными ФМн и АФМ сигналами). Высокоэффективные системы (I квадрант), позволяющие получить одновременно выигрыш по обоим показателям и на основе применения сложных сигнально-кодовых конструкций).

Можно выделить также два класса многопозиционных сигналов. К первому относятся так называемые «плотные» сигналы, когда с ростом объема ансамбля 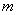при фиксированной размерности 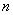расстояние между сигнальными точками уменьшается, а удельная скорость возрастает при соответствующем снижении энергетической эффективности . Примерами таких сигналов служат многопозиционные ФМн и АФМ.

Примером сигналов, у которых сигнальные векторы располагаются на прямой, являются двоичные противоположные сигналы ФМн-2. Им соответствует два симметрично расположенных относительно начала координат вектора дли-

300