Лекции по ТПС

Для получения передаточной функции рекурсивного фильтра принято использовать Z-преобразование:

или в компактном виде

B(z) Y(z) = A(z) X(z),

где A(z), B(z), X(z), Y(z) - Z-преобразования соответствующих числовых последовательностей.

Отсюда следует, что Z-преобразование передаточной функции фильтра (т.е. отношения выходной реакции ко входному воздействию) имеет вид:

271

(33.2)

После подстановки в (33.2) z exp( j Tд ) получим передаточную функцию в явном виде, т.е. в виде зависимости коэффициента передачи от частоты:

H д ( j ) H д (z exp( j Tд )) .

и

H д ( j ) A(z exp( j Tд )) ak exp( j nTд ) .

n

Расчет рекурсивных цифровых фильтров. Расчет (проектирование) ре-

курсивных фильтров существенно сложнее расчета нерекурсивных фильтров. Существует большое количество различных методик, основанных на методиках проектирования аналоговых фильтров и применении математического анализа, связанного с преобразованием Лапласа, Z-преобразованием, теории вычетов.

Рассмотрим наиболее простую и популярную методику, называемую «ча-

стотное преобразование».

Сущность этой методики состоит в трансформации передаточной характеристики H д (z* ) некоего ФНЧ, именуемого «ФНЧ-прототип», в передаточную характеристику H д (z) нужного фильтра (НЧ, ВЧ, полосового, режекторного), с последующей заменой z exp( j Tд ) .

Представим такую методику в виде последовательности “шагов”:

Шаг 1: Исходя из требований к качеству проектируемого фильтра (гладкость в полосе пропускания, фазовая характеристика, допустимый уровень пульсаций в полосах пропускания и запирания), выбирают тип фильтра и порядок фильтра N. При этом следует знать:

272

ФНЧ Баттерворта обеспечивает максимально плоскую характеристику в зоне пропускания, однако плохо передает фронты прямоугольных импульсов. Крутость переходной зоны (из полосы пропускания в полосу запирания) растет с увеличением N.

ФНЧ Бесселя обеспечивает линейность фазовой характеристики в зоне пропускания, что хорошо для фильтрации прямоугольных импульсов (малые выбросы на фронтах отфильтрованных импульсов), крутость переходной зоны меньшая, чем у фильтров Баттерворта.

ФНЧ Чебышева обеспечивает фиксированную пульсацию в зоне пропускания (фильтры типа I) или в зоне запирания (фильтры типа II). Плохо передает фронты прямоугольных импульсов. Крутость переходной зоны большая, чем у фильтров Баттерворта и Бесселя.

ФНЧ Кауэра имеет пульсацию как в зоне пропускания, так и в зоне запирания. Плохо передает фронты прямоугольных импульсов. Крутость переходной зоны большая, чем у фильтров Баттерворта и Бесселя.

Шаг 2. После выбора типа фильтра обращаются к одной из таблиц филь- тров-прототипов, из которых выбирают числовые значения коэффициентов ak и

bk . К таким таблицам «привязан» также числовой параметр fд* fc* - отношение частоты дискретизации к частоте среза фильтра-прототипа. В [1] предлагаются таблицы для fд* fc* 4 , имеющие вид:

Таблица 33.1. Коэффициенты для прототипов ФНЧ Баттерворта N-го порядка

Таблица 33.2. Коэффициенты для прототипов ФНЧ Бесселя N-го порядка

273

Таблица 33.3. Коэффициенты для прототипов ФНЧ Чебышева I-го типа N-го порядка с пульсацией 11% (1дБ)

Таблица 33.4. Коэффициенты для прототипов ФНЧ Кауэра N-го порядка

с пульсацией 15% (1,5дБ)

Рассматривая таблицы, нетрудно видеть что коэффициенты зависят также от некоего индекса i - номера каскада. Дело в том, что рекурсивные фильтры порядка N>2 принято получать путем последовательного соединения фильтров

274

2-го порядка. Поэтому если передаточная функция фильтра-прототипа 2-го порядка имеет вид:

то передаточная функция фильтра-прототипа более высокого порядка получается как произведение передаточных характеристик P частных фильтров:

чете полосового или режекторного фильтра), заменяют переменную z* на функцию переменной z , для чего используют соотношения из табл 33.5.

Таблица 33.5

275

Шаг 4. Полученное аналитическое выражение передаточной характеристики H д (z) упрощают так, чтобы в числителе и знаменателе оказались полиномы переменной z 1 .

Шаг 5. Числитель и знаменатель функции H д (z) делят на такое число, чтобы выполнялось условие b0 1. Результирующие коэффициенты в числителе и знаменателе (после такой нормировки) и образуют искомые множества коэффи-

как корень квадратный из суммы квадратов действительной и мнимой частей комплексной функции H д ( j ) .

В случае, когда АЧХ не устраивает пользователя, производят пересчет коэффициентов для другого типа фильтра либо увеличивают порядок фильтра.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Какой импульсной характеристикой обладают рекурсивные цифровые Фильтры (РЦФ)?

2.Какое преобразование используют для получения передаточной функции РЦФ?

3.В чем состоит сущность методики расчета РЦФ, называемой «частотное преобразование»?

4.Какими особенностями обладают РЦФ нижних частот Баттерворта, Чебышева, Кауэра, Бесселя?

5.Как получить рекурсивные фильтры порядка N>2 из фильтров 2-го по-

рядка?

276

РАЗДЕЛ 5. ПОМЕХОУСТОЙЧИВОСТЬ СИСТЕМ ПЕРЕДАЧИ

ДИСКРЕТНЫХ И НЕПРЕРЫВНЫХ СООБЩЕНИЙ

ЛЕКЦИЯ 34. ПОМЕХОУСТОЙЧИВОСТЬ РАЗЛИЧНЫХ ВИДОВ МОДУЛЯЦИИ ПРИ ПЕРЕДАЧЕ НЕПРЕРЫВНЫХ СООБЩЕНИЙ

С целью сравнения различных видов модуляции представляется естественным в качестве критерия выбрать величину вида:

,

где 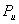- средняя мощность сообщения, - средние мощности сигнала и по-

мехи (в полосе сигнала) на входе приёмника. В случае белого гауссовского шума на входе приемника имеем:

.

Величина называется выигрыш модуляции. Однако использование не всегда оказывается удобным. Например, рассматриваются две системы передачи

информации (два метода модуляции) с полосами и соответственно. При

одинаковых , , и , т.е. при полной эквивалентности систем, имеем:

;

так что , если .

В этом смысле более удобно использование обобщенного выигрыша модуляции вида:

(34.1)

где – максимальная частота полосы частот, занимаемой сигналом.

277

Рассмотрим физический смысл величины . При непосредственной передаче сообщения (без модуляции) имеем:

.

При использовании модуляции:

.

Приравняем в обоих случаях:

,

откуда:

.

Таким образом, величина показывает, во сколько раз можно снизить среднюю мощность сигнала на входе приемника при использовании данного метода модуляции в сравнении с непосредственной передачей сообщения при од-

ном и том же .

Очевидно, что если исходить из одинаковых значений и , то ве-

личина показывает, во сколько раз возрастает величина при использовании данного метода модуляции в сравнении со случаем непосредственной

передачи сообщения. Наконец, отношение обобщенных выигрышей для двух различных методов модуляции показывает, во сколько раз можно снизить (повысить) среднюю мощность полезного сигнала при переходе от одного

метода модуляции к другому при сохранении одной и той же величины . Таким образом, величина характеризует энергетический выигрыш (проигрыш) одного метода модуляции по отношению к другому.

278

Представим в (34.1) в форме:

ПОМЕХОУСТОЙЧИВОСТЬ АНАЛОГОВЫХ МЕТОДОВ МОДУЛЯЦИИ

Амплитудная модуляция

;

.

Балансная модуляция

Однополосная модуляция

где - преобразование по Гильберту функции

Таким образом, во всех рассмотренных случаях модуляция не дает никакого выигрыша, либо (в случае АМ) приводит к энергетическим потерям вследствие бесполезной траты мощности на передачу несущей частоты. Следует также заметить, что в рассмотренных случаях полученные выражения являются

точными и справедливы при любых значениях .

Частотная модуляция

279

; ,

где - индекс ЧМ.

Это выражение справедливо в области , причем может принимать значения .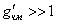

Однако увеличение связано с расширением полосы частот , поскольку для ЧМ:

.

При этом, с увеличением , увеличивается и , так что, начиная с некоторого значения , нарушается условие, при котором справедливо полу-

ченное выражение . При этом происходит резкое уменьшение величины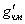

(пороговый эффект).

Введем понятие пороговой мощности сигнала 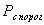. Если , то наступает пороговый эффект. Очевидно,

.

Наличие порогового эффекта при ЧМ иллюстрируется рис 34.1.

Рис.34.1

280