Лекции по ТПС

Принципиально под H t можно понимать любую линейную процедуру по переменной t : дифференцирование, интегрирование со скользящими пределами и т.п.

Итак, по данным наблюдения z(t) требуется определить оценку желаемого сигнала yˆ(t). Для того чтобы определить оптимальный в смысле наименьшей ковариационной матрицы оператор преобразования z(t) и yˆ(t) , воспользуемся принципом некогерентности погрешности оптимального оценивания к исходным данным. Другими словами, вся полезная информация, заключенная в исходных данных, должна быть исчерпана

t

l(t )K z ( )d Ryz ( ),

241

или

n(t) . Например, для решения уравнения Винера-Хопфа (28.4), позволяющего определить интегральную переходную функцию l(t) (или частотную характеристику), необходимо знать автокорреляционную функцию наблюдений K z ( ) и взаимную корреляционную функцию желаемого сигнала и наблюдений Ryz ( ).

Вместо них могут быть априорно заданы спектральные плотности этих сигналов или дифференциальные уравнения, решения которых суть случайные функции с заданными характеристиками. В последнем случае динамическая система называется формирующим фильтром. Например, для задания случайного процесса с автокорреляционной функцией

Kx ( ) 2e

и со спектральной плотностью

нужно иметь формирующий фильтр, заданный уравнением первого порядка x x q,

где q – «белый шум» с интенсивностью

Q 2 2 .

Формирующим фильтром является стационарная многоканальная система, подчиняющаяся матричному дифференциальному уравнению

функциями типа «белый шум». Можно показать, что при условии асимптотической устойчивости формирующего фильтра корреляционные функции всех составляющих вектора x(t) и их взаимные корреляционные функции определяют-

тральные плотности, соответствующие этим корреляционным функциям, имеют вид отношений полиномов от четных степеней частоты.

Уравнение Винера-Хопфа (28.4) имеет строгое аналитическое решение для так называемых марковских процессов различного порядка. Таким образом, представление формирующего фильтра в виде дифференциального уравнения (28.5) является достаточно универсальным, хотя существуют в природе процессы, которые не могут быть представлены таким образом.

Формирующий фильтр (28.5) может «генерировать» и такие сигналы, которые нельзя отнести к стационарным случайным процессам. Иллюстрацией к этому может служить так называемая «модель дрейфа»

x1 (t) x2 (t), x2 (t) x3 (t), x3 (t) 0,

z(t) x1 (t) n(t).

Эта система наблюдаема, хотя наблюдения содержат шум. Видим, что x3 (t) const . Пусть x3 (t) 2a0 , тогда

x2 (t) a1 2a0t,

x1(t) a2 a1t a0t 2.

Неизвестные постоянные составляющие определяют из наблюдений методом наименьших квадратов.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Что понимается под операцией фильтрации сигнала?

2.В чем заключаются операции сглаживания и экстраполирования?

3.Какими исходными данными необходимо располагать для решения уравнения Винера-Хопфа?

4.Что понимается под формирующим фильтром?

5.Для каких случайных процессов имеет решение уравнение Винера-

Хопфа?

243

ЛЕКЦИЯ 29. ФИЛЬТР КАЛМАНА ДЛЯ ДИСКРЕТНЫХ НАБЛЮДЕНИЙ И ДИСКРЕТНОЙ МОДЕЛИ СИГНАЛА

В предыдущих лекциях упоминалась задача оценивания параметра сигнала, не изменяющегося в течение времени наблюдения, равного длительности сигнала. Однако во многих случаях нельзя пренебречь изменением этого параметра. К ним относятся, например, задачи построения следящих систем в радиолокации, радионавигации и радиосвязи, автоматики. В таких системах время наблюдения, как правило, велико, и основной целью анализа последовательно-

сти отсчётов является оценка каких-либо изменяющихся параметров движения объектов или параметров помех, необходимая для обеспечения надежного функционирования системы. При этом с каждым очередным наблю-

ной с сигналом помехи.

В подобных задачах принципиальное значение имеет описание процесса изменения параметра в дискретном времени.

Рассмотрим возможности построения рекуррентных оценок параметра сигнала, представляющего собой марковский случайный процесс, заданных стохастическими разностными уравнениями. Для этого вначале попытаемся решить наиболее простую задачу оценивания скалярной авторегрессионной последовательности

244

цесса. Для дискретного сигнала, представляющего дискретный случайный

Для всех видов задач особый интерес представляют эффективные, с точки зрения вычислений, рекуррентные оценки, которые удается представить в

.

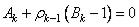, получаем формулу

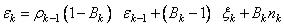, (29.2)

в которой отражены три составляющие ошибки оценивания на -м шаге.

Первое слагаемое учитывает ошибку на предыдущем шаге. Второе определяется величиной изменения параметра, т.е.

245

динамикой случайного процесса. Составляющая ошибки связана с по-

мехой , возникающей при наблюдении . Поскольку все слагаемые (29.2) являются независимыми случайными величинами, то дисперсия ошибки фильтрации будет равна сумме

,

где . В уравнении (29.3) величина является экстраполированной на один шаг оценкой параметра (прогнозом 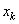) на основе наблюдений . Действительно, до наблюдения имеется

лишь оценка и описание одношагового изменения пара-

метра. Поскольку – последовательность независимых случайных вели-

чин, то лучшим прогнозом будет 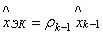. Дисперсия ошибки прогноза

в точности равна . Такой же вывод следует из формулы (2.36) для диспер-

сии ошибки оценивания, если положить . В этом случае 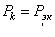, по-

246

приводит к уменьшению дисперсии прогноза.

С учетом приведенных рассуждений определим начальные условия

для алгоритма (29.5). До первого наблюдения 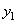известно, что подчиняется нормальному закону распределения с нулевым средним и дисперси-

Анализируя вывод алгоритма фильтрации (29.3), необходимо заметить,

что представление текущей оценки в виде линейной комбинации предше-

ствующей оценки и очередного наблюдения 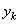резко ограничивает класс возможных процедур. В связи с этим полученный результат (29.3) может рассматриваться как наилучшее (в смысле минимума дисперсии ошибки) правило лишь в довольно узком классе рекуррентных алгоритмов оценивания изменяющегося параметра.

Замечательным достижением Р.Калмана и Р.Бьюси было доказательство строгой оптимальности алгоритма (29.3) в классе любых (не только рекур-

рентных) процедур оценивания параметра , заданного скалярными или векторными уравнениями авторегрессии. Поэтому рекуррентное правило оценивания (29.3), а также его многомерные обобщения, часто называют фильтром Калмана.

247

Рис. 29.1. Структурная схема фильтра Калмана

Анализ соотношения (29.3) и соответствующей ему структурной схемы на рис.29.1 показывает, что в фильтре Калмана реализуется идея предсказа-

ния-коррекции. Предыдущая оценка экстраполируется на один шаг впе-

ред и затем используется для получения оптимальной оценки . При этом из очередного наблюдения вычитается экстраполированное значение 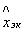и определяется сигнал ошибки , включающий в себя ошибку прогноза и погрешность наблюдения. После умножения сум-

марной ошибки на коэффициент 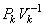, учитывающий дисперсию каждого

из слагаемых, образуется сигнал коррекции. Результирующая оценка 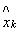получается после добавления сигнала коррекции к экстраполированному зна-

чению .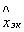

Для иллюстрации особенностей рекуррентного оценивания рассмотрим

зависимости дисперсий ошибки от номера шага , показанные на рис.29.2. При расчетах предполагалось, что изменение парамет-

248

ей (рис. 29.2,а) или нестационарный случайный процесс

с изменяющейся на каждом шаге дисперсией (рис.29.2, б). До начала наблюдений наилучшей оценкой является математическое ожида-

ние с дисперсией . После первого шага дисперсия ошибки уменьшается: . Затем вычисляется дисперсия ошибки

экстраполяции для второго шага наблюдений и т.д. Как следует из графиков рис.29.2,а, при стационарных наблюдениях по мере роста дисперсия ошибки стремится к некоторому установившемуся значению. Если же

гов 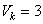, а для нечетных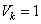, то зависимость величины 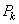от номера шага также носит колебательный характер (рис.29.2, б).

Рис. 29.2. Изменение дисперсии ошибки на первых шагах фильтрации при стационарном (а) и нестационарном (б) шуме

Поскольку установившийся режим часто является основным для фильтра Калмана, рассмотрим этот случай более подробно. При постоянных па-

249

ние . Положительное решение можно записать в виде:

где – отношение дисперсии полезного параметра к дисперсии шума.

На рис.29.3 представлено семейство зависимостей относительной дисперсии ошибки фильтрации в установившемся режиме от величины коэффициента корреляции соседних значений оцениваемого параметра. Как видно из графиков, для получения малых ошибок необходимы либо большие отношения сигнал/шум , либо близкие к единице коэффициенты корреляции . При приведенные графики асимптотически приближаются к прямым линиям с одинаковым наклоном в логарифмическом масштабе (рис.29.3). Для этого случая уравнение (29.5) упрощается:

.

Рис.29.3. Дисперсия ошибки фильтра Калмана

250