Лекции по ТПС

+

Рис. 25.9 Согласованный фильтр сигнала Баркера с N = 7

М – последовательности

Среди фазоманипулированных сигналов особое значение занимают сигналы, кодовые последовательности которых являются последовательностями максимальной длины или М - последовательностями.

М – последовательности принадлежат к разряду двоичных линейных рекуррентных последовательностей и представляют собой набор N периодически повторяющихся двоичных символов. Причем каждый текущий символ dj образуется в результате сложения по модулю 2 некоторого числа m предыдущих символов, одни из которых умножаются на 1, а другие – на 0.

Для j-го символа имеем:

Где а1…аm – числа 0 или 1.

Технически генератор М-последовательности строится в виде регистра (последовательно включенных триггеров) с отводами, с цепью обратной связи и с сумматором по модулю 2. Пример такого генератора приведен на рисунке 25.10. Умножение на а1…аm в (4) означает просто наличие или отсутствие отвода, т.е. связи соответствующего триггера (разряда регистра) с сумматором. В m- разрядном регистре максимальный период равен: Nm – 1. Величина m называется памятью последовательности. Если отводы выбраны произвольно, то не всегда на выходе генератора будет наблюдаться последовательность максимальной длины. Правило выбора отводов, позволяющее получить последовательность с периодом Nm-1, предполагает найти неприводимые примитивные полиномы степени m с коэффициентами, равными 0 и 1. Не равные нулю коэффициенты в полиномах определяют номера отводов в регистре.

211

Так, при m=6 существует 3 примитивных многочлена:

На рисунке 25.10 реализован первый вариант.

Рис.25.10 Генератор М-последовательности с периодом N = 26 – 1 = 63

Особенности автокорреляционной функции М-последовательности

Наибольший интерес представляет нормированная автокорреляционная функция (АКФ). Различают два случая получения такой функции: в периодическом (ПАКФ) и апериодическом режимах. Периодическая АКФ имеет основной, равный единице, пик и ряд боковых выбросов, амплитуды которых 1/N. С ростом N ПАКФ приближается к идеальной, когда боковые пики становятся по сравнения с основным пренебрежимо малы.

Боковые пики АКФ в апериодическом режиме существенно больше боковых пиков ПАКФ. Среднеквадратичное значение боковых пиков (вычисленное

через дисперсию) равно 1/2 0,4/ N .

Усеченные М-последовательности

Разбивая М-последовательность (полный период N) на сегменты длительности Nс, можно получить большое число ШПС, рассматривая каждый из сегментов как самостоятельный сигнал. Если сегменты не перекрываются, то их число равно n = N/(Nc-1). Таким образом, можно получить большое число псевдослучайных последовательностей. Автокорреляционные свойства таких последовательностей значительно хуже, чем у М-последовательности той же длитель-

212

ности и зависят от Nc. Установленно, что у 90% сегментов uб 3 / N c , а у 50%

- 2 / N c .

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Какие сигналы называют широкополосными?

2.В чем преимущество использования широкополосных сигналов?

3.Какие существуют виды широкополосных сигналов?

4.От чего зависит помехоустойчивость широкополосных сигналов?

5.Какие из широкополосных сигналов наиболее чаще применяются в системах передачи информации?

РАЗДЕЛ 4. ОСНОВЫ ТЕОРИИ ОПТИМАЛЬНОГО ПРИЕМА СИГНАЛОВ НА ФОНЕ ПОМЕХ

ЛЕКЦИЯ 26. ЗАДАЧИ ПРИЕМА. КОРРЕЛЯЦИОННЫЕ ПРИЕМНИКИ И СОГЛАСОВАННЫЕ ФИЛЬТРЫ

Задачи оптимального приема

Теория передачи сигналов подразумевает теоретическое обоснование способов и методов передачи информации от источника к получателю с помощью какого-либо переносчика, в частности, радиосигнала. Радиосигнал, как носитель полезной информации, в канале связи от передатчика к приемнику претерпевает изменения, вызванные искажениями при передаче, влиянием помех в канале связи, искажениями при приеме. Если в точке передачи сигнала достаточно просто проконтролировать и откорректировать передаваемый сигнал с целью снижения искажения передатчика, то в точке приема приходится иметь дело с сигналом, искаженным каналом связи случайным образом и по не зависящим от нас обстоятельствам, что приводит к необходимости применять особые способы приема сигнала для снижения возможных ошибок в передаче информации (оптимальный прием сигналов).

Принимаемый сигнал имеет часть параметров, известных априорно (т.е. до передачи). Если известны все параметры сигнала, то нет смысла его принимать (он известен); если все параметры сигнала заранее неизвестны, то принять и выделить его на фоне помех не представляется возможным (неизвестно, что выделять). При малом объеме априорных данных необходимо пользоваться методами адаптивного приема.

213

Оптимальный (идеальный) прием сигналов, обеспечивающий минимальные искажения сообщения, реализуется оптимальный приемником, работающим по оптимальному алгоритму, основанному на априорной информации и выбранных критериях оптимальности.

Оптимальный приемник, который обеспечивает минимальный уровень искажений, принято называть потенциально помехоустойчивым. По определению, помехоустойчивость реальных приемников не может превышать потенциальную для заданных условий, а только приближаться к ней. Сравнивая помехоустойчивость реальных приемников с потенциальной помехоустойчивостью, можно выяснить степень технического совершенства реальных приемников и возможные резервы повышения их помехоустойчивости. Сравнивая значения потенциальной помехоустойчивости при различных видах сигналов, можно определить наилучшие виды передаваемых сигналов.

Решение основных проблем теории оптимального радиоприема базируется на хорошо разработанных методах математической статистики, разработанных А.Н.Колмогоровым, Н.Винером, В.А.Котельниковым и др.

В зависимости от целевого назначения и условий работы различают четыре задачи, решаемых в теории оптимальных методов радиоприема.

Будем рассматривать аддитивную смесь сигнала и помехи:

y(t) = s(t, λ) + n(t),

где λ = λ{λ1...λm} – параметры, от которых зависит сигнал;

n(t) – аддитивная помеха, в общем случае представляется моделью белого нормального центрированного шума.

1. Обнаружение сигнала известной формы (детерминированного сигнала).

Пусть неизвестен сам факт наличия или отсутствия сигнала s(t, λ) в принятом колебании y(t), т.е.

здесь - случайная величина на два значения 0, 1.

Необходимо оценить значение дискретного параметра . В результате решения должна быть получена структурная схема оптимального обнаружения сигнала и определены его количественные характеристики.

2. Различение сигналов известной формы.

214

Предположим, что в принятом колебании y(t) может быть только один из двух сигналов:

Эта задача характерна для систем передачи бинарных сигналов, в частности, в телеграфии. Возможна постановка задачи для большего количества сигналов (радиосвязь, телеуправление).

3. Оценка параметров сигнала.

Пусть какой-нибудь параметр хi сигнала s(t, λ) является случайной величиной с априорной плотностью вероятности Popr(xi). Необходимо с минимальной погрешностью определить значение этого параметра λi в принятой реализации y(t). Это простейшая задача оценки параметров сигнала. Возможна постановка задачи о совместной оценке двух и более параметров. Такие задачи характерны для измерительной техники, радиолокации, радионавигации.

4. Фильтрация сообщений.

Пусть интересующий нас параметр λi полезного сигнала s(t, λ) зависит от времени и представляет собой информационное сообщение – случайный процесс λi(t) с известными статистическими характеристиками. Располагая сведениями о помехе n(t), нужно получить (отфильтровать, выделить наилучшим образом)

оценку ˆ i (t) реализации случайного сообщения λi(t), содержащейся в наблюдаемой реализации y(t).

Задача фильтрации переходит в задачу оценки параметра сигнала, если оцениваемый параметр за время наблюдения Т не успевает существенно измениться.

Задачи фильтрации возникают в радиосвязи и телеметрии (выделение речевого или какого-либо другого сообщения), в телевидении (выделение телевизионного сообщения) и т.д.

Оптимальными приемниками при решении задач обнаружения и различения таких сигналов являются корреляционные приемники и согласованные фильтры, способные обеспечить максимальное отношение сигнал-помеха на выходе приемника при условии, что помеха, действующая на входе приемника, является аддитивной и гауссовской. Поскольку достигаемый ими результат основан на свойствах функции взаимной корреляции между принятым колебанием y(t) и ожидаемым сигналом s(t) на приеме, которая обращается в функцию авто-

215

корреляции при наличии сигнала s(t) в y(t), становится понятным, что форма сигнала на выходе таких приемников не сохраняется.

Согласованный фильтр представляет собой четырехполюсник с линейной зависимостью между напряжением на входе и выходе, импульсная характеристика h(t) которого является реакцией на дельта-импульс и зависит только от параметров и вида четырехполюсника. При воздействии сигнала s(t) на входе четырехполюсника с импульсной характеристикой h(t) сигнал на его выходе определяется интегралом свертки s(τ) и h(t )

sв ых t s h t d

Если импульсная характеристика четырехполюсника s(t ) представляет собой с точностью до постоянного множителя с зеркальное отображение детерминированного сигнала s(t), рисунок 26.1, то сигнал на выходе четырехполюсника определяется сверткой s(t) и cs(t )

которая в данном случае совпадает с функцией автокорреляции, характеризующей взаимосвязь между сигналом s( ) и его зеркальным отображением cs(t ) , сдвинутых на время t . Это означает, что сигнал sвых(t) на выходе четырехполюсника обладает свойствами функции автокорреляции: действует на интервале времени, равном удвоенной длительности сигнала ; симметричен относительно момента времени t t0 , равного длительности сигнала tc; имеет максимум в этот момент времени, численно равный энергии сигнала.

216

Рис.26.1

Четырехполюсник с импульсной характеристикой, являющейся зеркальным отображением детерминированного сигнала, принято называть фильтром, согласованным с этим сигналом или линейным согласованным фильтром (ЛСФ).

При поступлении на вход фильтра сигнала, с которым он не согласован, на его выходе действует сигнал sвых(t), обладающий свойствами функции взаимной корреляции: отсутствием симметрии относительно момента времени t0, равного длительности сигнала tc, максимумом, приходящимся на любой другой момент времени не равным энергии сигнала.

Таким образом, согласованный фильтр, как и корреляционный приемник, вычисляет взаимную корреляцию принятого и ожидаемого полезного сигналов. Различие между ними состоит в том, что в корреляционном приемнике ожидаемый полезный сигнал вырабатывается с помощью опорного генератора в определенные моменты времени, а в согласованном фильтре ожидаемый полезный сигнал представляет собой импульсную характеристику фильтра неизменную во времени, что обеспечивает инвариантность ЛСФ относительно момента прихода сигнала.

Применение нескольких фильтров, каждый из которых согласован с одним из детерминированных сигналов, позволяет построить приемник для различения сигналов известной формы.

Передаточная функция K(j ) согласованного фильтра определяется прямым преобразованием Фурье от импульсной характеристики фильтра s(tс )

K ( j ) c s(tc t)e j t dt c S ( j )e j tc (26.2)

и представляет собой комплексно-сопряженный спектр напряжения сигнала s(t), с которым фильтр согласован.

Из (26.2) следует, что амплитудно-частотная характеристика фильтра определяется амплитудным спектром сигнала s(t)

K ( j ) c S( j ) .

Фазо-частотная характеристика фильтра ( ) противоположна по знаку фа- зо-частотной характеристике ( ) сигнала s(t)

( ) ( ) tc .

217

С учетом (26.3), (26.4) соотношение (26.5) примет вид

Допустим, что помеха представляет собой аддитивный белый гауссовский шум со спектральной плотностью мощности N0/2. Тогда, учитывая, что энергия сигнала связана со спектральной плотностью мощности сигнала теоремой Рэлея

E 1 S ( )d

c 2 м

соотношение (10.6) примет вид

Выражение (26.7) показывает, что отношение сигнал/помеха на выходе фильтра определяется только энергией сигнала и спектральной плотностью мощности белого шума и не зависит от формы сигнала. Это отношение является наилучшим – оптимальным в классе линейных фильтров по критерию сигнал/помеха.

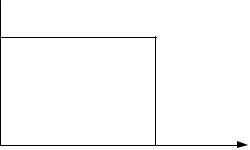
Рассмотрим примеры согласованных фильтров.

Фильтр, согласованный с прямоугольным импульсом постоянного то-

ка. Для передачи данных часто используются импульсы постоянного тока (рис.

26.2).

219

U

А=1

Рис.26.2

Рассмотрим пример построения фильтра, согласованного с такими импульсами.

Спектральная плотность напряжения сигнала определяется как прямое преобразование Фурье от формы импульса s(t)

Передаточная функция фильтра в соответствии с (10.2) имеет вид

Из сравнения (26.8) и (26.9) видно, передаточная функция фильтра совпадает со спектральной плотностью напряжения прямоугольного импульса S( j ) .

Передаточную функцию фильтра представим в виде двух сомножителей:

K ( j ) K1 ( j ) K2 ( j )

грирующей цепи, рис. 26.3. Передаточной функции K 2 ( j ) соответствует параллельная цепь с линией задержки на время Т и вычитающее устройство.

220