Лекции по ТПС

Качество работы декодера зависит от длины блока декодирования - L (ширины окна декодирования), причём чем больше блок декодирования, тем лучше.

Свободным кодовым расстоянием сверточного кода называется d = max dL, которое равно наименьшему весу ненулевого начального блока декодирования при L , обычно свободное кодовое расстояние d (n - k).

Методы кодирования и декодирования. Кодирование свёрточных кодов производится аналогично блочным циклическим кодам с помощью регистров сдвига, у которых структура обратных связей определяется производящим полиномом. Различие состоит в том, что при k0 >1 свёрточный код имеет несколько производящих полиномов и кодер должен иметь соответствующее число регистров сдвига.

На рисунке 21.1 показана структурная кодера свёрточного несистематического кода R=1/2 с использованием двух производящих полиномов.

На вход регистра сдвига кодера из 3 ячеек памяти подаётся двоичная последовательность информационных символов, из которых с помощью регистра сдвига и сумматоров по модулю 2 формируется две двоичных последовательности. Символы этих последовательностей с помощью ключа К поочерёдно подключаются к выходу кодера; скорость переключения должна быть в два раза больше скорости ввода информационных символов.

Если свёрточный код является систематическим, то g1(x) = 1 и в кодере, рисунок 21.1, отсутствует верхний сумматор и информационная последовательность становится частью выходной последовательности без кодирования, что упрощает в последующем процесс её декодирования.

Для декодирования свёрточных кодов используется алгоритм Витерби, последовательное декодирование и синдромное декодирование.

Декодирование по алгоритму Витерби и последовательное декодирование являются оптимальными по критерию максимального правдоподобия и широко используются для двоичных сверточных кодов с малой длиной кодового ограничения в двоичных каналах и каналах с многоуровневыми сигналами.

При реализации алгоритма Витерби возникают определенные трудности, которые связаны с тем, что сложность декодера экспоненциально растет с увеличением кодового ограничения (число состояний декодера равно 2n-1); поэтому значение кодового ограничения кодов, применяемых на практике, не превышает nа 10.

В отличие от алгоритма Витерби при последовательном декодировании производится продолжение и обновление метрики только одного пути, который представляется наиболее вероятным, при этом делается попытка принять реше-

171

ние о декодируемом символе, принятом в начале пути. Если решение принять невозможно (в соответствии с заданным правилом), производится либо движение вперёд, то есть прием очередного символа и обработка метрики данного пути, или возврат назад, если движение вперёд по данному пути является ошибочным (значения метрики увеличиваются). Декодер двигается вперёд и назад, пробуя различные пути, до тех пор, пока не будет принято решение о декодировании символа, расположенного в начале пути.

Основное достоинство последовательного алгоритма заключается в том, что в среднем длина пути, достаточная для правильного декодирования меньше, чем у алгоритма Витерби. Недостатки определяются тем, что длина пути, приводящего к правильному декодированию, является случайной величиной.

Это вызывает затруднения при реализации декодера, так как нельзя определить заранее какой объём памяти потребуется для сохранения метрики рассматриваемого пути, а это значит, что всегда существует вероятность переполнения памяти и сбой декодера.

В практике построения последовательных декодеров применяются два варианта алгоритма последовательного декодирования, позволяющих получить приемлемые для реализации сложность декодирования и объём памяти: алгоритм Фэно и стек-алгоритм. Первый был предложен Р. Фэно в 1963 г. и неоднократно усовершенствовался. Наиболее совершенным считается алгоритм максимального правдоподобия, предложенный К.Ш. Зигангировым и У. Дженилеком, получивший название стек-алгоритм. Эффективность алгоритмов и сложность декодирующих устройств во многом зависит от предъявляемых к ним требований работы в реальном времени.

Перемежение символов. Рассмотренные примеры помехоустойчивых кодов наглядно показывают степень нарастания сложности декодирования при переходе от обнаружения и исправления одиночных ошибок к исправлению пакетов ошибок. Учитывая, что всегда существует вероятность возникновения в канале ошибки такой кратности или пакета ошибок, которые декодер не способен обнаружить и исправить, возникает необходимость в разработке эффективных мер по борьбе с ними преимущественно в каналах радиосвязи. Одним из способов преобразования пакетов ошибок в независимые ошибки является применение устройств перемежения. Перемежение символов передаваемой последовательности состоит в том, что подлежащая передаче кодовая последовательность a11,a12,a13… длины п=n1n2 записывается по строкам в матрицу размером n1n2

172

затем считывается по столбцам в виде последовательности и передается в канал. В результате символы сообщения a11,a12,a13…, которые в исходной последовательности следовали друг за другом, передаются в канал с интервалом n2 символов, который называется глубиной перемежения. Увеличение глубины перемежения повышает эффективность сверточного кодирования, но приводит к задержке передаваемых символов и требует определенного объема памяти устройства перемежения.

На выходе канала происходит обратная перезапись принятой последовательности символов. Запись осуществляется по столбцам, считывание — по строкам. В восстановленной последовательности a11,a12,a13… пакетом ошибок оказываются искажены несмежные, разбросанные по всей длине п=n1n2 символы, что упрощает их исправление сверточным кодом. Существуют различные варианты построения перемежителей, которые используются при каскадном кодировании и турбо кодах.

ПРИМЕНЕНИЕ ПОМЕХОУСТОЙЧИВЫХ КОДОВ В СИСТЕМАХ

ЖЕЛЕЗНОДОРОЖНОЙ АВТОМАТИКИ, ТЕЛЕМЕХАНИКИ И СВЯЗИ

Помехоустойчивые коды в системах ЖАТС используются преимущественно для обнаружения ошибок различной кратности. Это обусловлено во многом спецификой работы систем ЖАТ, отвечающих за безопасность движения поездов.

Всистемах телемеханики используются корректирующие коды с постоянным весом. Кодовые комбинации таких кодов содержат постоянное число единиц и нулей. Общее число разрешенных комбинаций определяется числом сочетаний Cnm, где n — число символов в кодовой комбинации, m— число единиц в ней. Поэтому эти коды называют также кодами на одно сочетание. Коды имеют минимальное кодовое расстояние dmin=2 и обнаруживают однократные ошибки.

Вагрегатной системе диспетчерской централизации (АСДЦ) для обнаружения ошибок используются систематические помехоустойчивые коды: код Бауэ-

173

ра, являющийся разновидностью кода с простым повторением, и код с одной проверкой на нечетность (проверкой по паритету). Принцип кодирования кодом Бауэра состоит в повторении информационной последовательности из k символов, если она содержит нечетное число единиц, и инверсном повторении информационных символов — при четном числе единиц. Например, информационным последовательностям 0111 и 0101 соответствуют кодовые комбинации U1 =01110111 и U2 =01011010. Избыточность кода Бауэра равна 0,5.

Вкомбинациях кода с проверкой на нечетность используется один проверочный символ, при сложении которого с информационными символами по модулю 2 их сумма равняется единице.

Вцифровых системах связи, радиосвязи, микропроцессорных системах ЖАТ, протоколах передачи данных для обнаружения ошибок применяются циклические избыточные коды (CRC — Cyclic Redundancy Check). Коды предназначены для вычисления контрольной суммы, являющейся остатком при делении полинома, соответствующего передаваемой двоичной последовательности, на производящий полином.

Принцип циклической проверки CRC кодами аналогичен принципам кодирования и декодирования циклических кодов и состоит в следующем. На передающей станции определяется остаток от деления информационного полинома (информационной последовательности) на производящий многочлен g(x), который в виде проверочных символов передается после информационных символов в общем блоке данных. На приемной станции выполняется деление принятой последовательности на g(x), и в случае получения остатка отделения принимается решение о наличии ошибки.

В качестве производящего полинома в CRC кодах используются неприводимые полиномы до 32 - й степени включительно (примеры полиномов приведены в таблице 19.2).

Возможности CRC кодов используются для обнаружения ошибок различной кратности и пакетов ошибок.

Например, в модемных протоколах коррекции ошибок и протоколах каналов передачи кадров в сетях передачи данных используется код CRC-16. Код имеет минимальное кодовое расстояние dmin = 4 и позволяет обнаруживать ошибки до третьей кратности включительно и пакеты ошибок длиной до 16символов, ошибки нечетной кратности.

174

Другим примером является применение кода CRC- 4 в цифровых системах передачи для обеспечения контроля цикловой синхронизации.

Для защиты от ошибок в радиоканалах подвижной связи стандарта GSM используются циклические и сверточные коды в сочетании с перемежением, представляющие собой один из вариантов каскадного кодирования— декодирования.

Для исправления независимых ошибок в полноскоростных каналах связи систем GSM используется сверточный код со скоростью 1/2 и к = 5. Декодирование сверточного кода осуществляется по алгоритму Витерби.

В радиоканалах подвижной связи стандарта TETRA используется блочное, сверточное кодирование в сочетании с перемежением и шифрованием.

Широкое применение помехоустойчивые коды нашли в технологиях радиодоступа. Так, например, в технологии WIMAX применяется сверточное кодирование, сверточное турбокодирование (CTC — Convolution Turbo Code) с переменной скоростью кода и повторным кодированием; блочное турбокодирование (BTC — Block Turbo Code); кодирование низкой плотности с проверкой на чет-

ность (LDPC — Low Density Parity Check Code).

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Что означает термин «свертка» в теории сверточных кодов?

2.Способы задания сверточных кодов.

3.Что понимается под свободным кодовым расстоянием?

4.Способы декодирования сверточных кодов.

5.Для чего применяется операция перемежения кодовых символов?

РАЗДЕЛ 3. ЭЛЕМЕНТЫ ТЕОРИИ МОДУЛЯЦИИ И ДЕТЕКТИРОВАНИЯ

ЛЕКЦИЯ 22. МОДУЛИРОВАННЫЕ КОЛЕБАНИЯ И ИХ СПЕКТРЫ

Модуляция заключается в изменении одного или нескольких параметров сигнала переносчика в соответствии с передаваемым сообщением. При использовании в качестве переносчика высокочастотного гармонического колебания модулированный сигнал в общем случае можно представить в виде

s(t) a(t)cos[ (t)t (t)]. (22.1)

175

В зависимости от того, какой из параметров а, ω или φ модулируется, различают три вида модуляции: амплитудную (АМ), частотную (ЧМ) и фазовую (ФМ). Всякое модулированное колебание несинусоидально и имеет сложный спектр. Из сказанного следует, что такие виды модуляции как импульснокодовая и дельта-модуляция не являются таковыми исходя из определения понятия «модуляция».

Рассмотрим перечисленные выше виды классической модуляции более подробно.

АМПЛИТУДНАЯ МОДУЛЯЦИЯ

При амплитудной модуляции по закону управляющего сигнала и(t) изменяется амплитуда колебаний:

a(t) a0 a u(t) a0 [1 mu(t)] (22.2)

тельное изменение амплитуды, называемое коэффициентом модуляции.

АМ колебание записывается в виде

s(t) a0 [1 mu(t)]cos( 0t 0 ) (22.3)

и для случая модуляции чистым тоном (u(t) cos t) имеет вид, показанный на рис.2.8. Очевидно, чтобы не было искажений, коэффициент модуляции должен быть меньше единицы. Из графика для АМ колебаний видно, что

amin a0 (1 m)

176

amax a0 (1 m)

откуда имеем

Определим спектр АМ колебаний при модуляции чистым тоном. Это можно сделать с помощью преобразования Фурье. Однако проще его получить с помощью простых тригонометрических преобразований. Действительно, полагая и(t)=соsΩt, получим

рые называются боковыми частотами. Спектр АМ колебания показан на рис. 22.1. Ширина спектра АМ-сигнала равна 2 .

Рис.22.1

Как известно, гармонические колебания часто представляв в виде векторов. Аналогично можно построить векторную диаграмму для АМ колебания, которая показана на рис.22.2.

177

Рис.22.2

При построении диаграммы предполагалось, что плоскость чертежа вращается по часовой стрелке со скоростью 0 . Поэтому вектор несущего колебания ОА неподвижен относительно оси времени. Векторы боковых колебаний вращаются относительно вектора несущей со скоростью , т.е. в противоположные стороны. Результирующий вектор ОС в результате этого изменяется только по длине, но не по направлению.

В более общем случае, когда модуляция осуществляется сложным периодическим сигналом, который можно разложить в ряд Фурье

выражение для АМ - колебания можно представить в виде

m k )t

2 k 1

Вэтом случае АМ колебание состоит из колебания несущей частоты 0 и

двух боковых полос с суммарными 0 k и разностными 0 k частотами. Спектр такого колебания показан на рис.22.3.cos[( 0ck k0 0 ].a

Рис.22.3

178

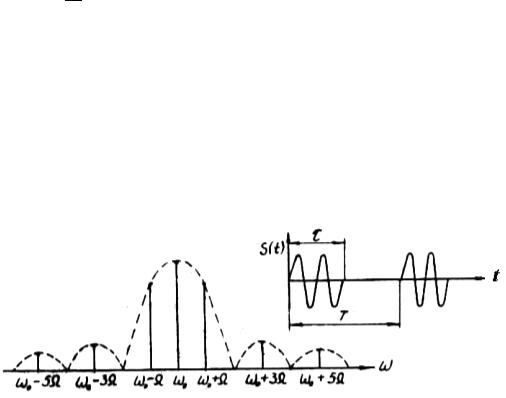
Если спектр модулирующего колебания ограничен сверху частотой ширина спектра модулированного колебания равна 2Fmax

Заметим, что огибающая амплитуд боковых частот с точностью до постоян-

ного множителя m2 a0 , совпадает с огибающей спектра амплитуд модулирующей

функции. Это позволяет легко построить амплитудный спектр АМ колебания, если известен спектр модулирующей функции. Для построения необходимо сместить спектр модулирующей функции по оси частот на величину 0 , получая при этом верхнюю боковую полосу; нижняя боковая полоса будет являться зеркальным отображением верхней относительно частоты 0 .

Проиллюстрируем сказанное на примере амплитудной манипуляции,

рис.22.4.

Рис.22.4

В случае манипуляции модулирующая функция представляет собой периодиче-

Амплитудно-манипулированное колебание при этом записывается в виде

179

Амплитудный спектр манипулированного колебания показан на рис.22.4.

Амплитудно-модулированные колебания являются типичным примером почти периодических сигналов, для которых гармонические составляющие имеют некратные частоты.

Рассмотрим энергетические соотношения при АМ. В соответствии с изменением амплитуды колебания изменяется и средняя за период высокой частоты мощность модулированного колебания.

Мощность сигнала в отсутствии модуляции (мощность несущего колебания) определяется первым членом выражения (22.5) и равна

где T0 2 – период высокочастотного колебания.

0

В режиме модуляции мощность непрерывно изменяется. Ее максимальное и минимальное значения соответственно определяется выражениями

Средняя за период модуляции мощность будет равна

180