Лекции по ТПС

Рис. 20.1

Схемы содержат три триггера (S1,S2,S3), число которых определяется старшей степенью полинома g(х), образующих регистр сдвига, и двух сумматоров по mod2 – по числу знаков сложения в g(х).

Представим полином g(х) в виде g(х)=g0х0+g1х1+g2х2+g3х3 (где g0=g1=g3=1; g2=0) и рассмотрим работу схемы кодера несистематического кода (схема умножения), рис. 20.1. Функционирование схемы определяется уравнениями: S1=Dl; S2=DS1; S3=DS2; U=l+S2+S3, где символом D обозначена запаздывание в работе триггера на один такт. Работа схемы при поступлении на ее вход комбинации l отображена в таблице 20.2, исходное состояние триггеров - нулевое.

Схема не содержит цепей обратной связи, поэтому может давать на выходе импульсы не более (n-k) тактов после подачи последнего импульса на ее вход, комбинация на выходе схемы представляет собой реакцию схемы на входное воздействие в виде последовательности l.

161

В отличие от нее схема кодера систематического кода представляет собой регистр сдвига с обратными связями, то есть является схемой деления на полином g(х). Функционирование схемы кодера, рис.20.2, определяется уравнениями: S1=D(l+ S2+ S3); S2=DS1; S3=DS2, когда первые k тактов ключ К находится в положении 1. Последующие (n-k) тактов, когда ключ К находится в положении 2, на выход схемы подается результат сложения S2+S3.

S1 S2 S3

+ +

2

К

1 L

Рис. 20.2

Работа схемы при поступлении на ее вход комбинации l отображена в таб-

лице 20.3.

Декодирование циклических кодов. Декодирование кодовой комбина-

ции циклического кода осуществляется в два этапа: на первом этапе выполняется обнаружение ошибки (в некоторых системах передачи на этом процесс декодирования завершается), на втором этапе осуществляется исправление ошибки.

Первый этап состоит в делении кодовой комбинации на производящий полином: по определению циклического кода любая кодовая комбинация, принадлежащая коду, кратна производящему полиному. Если деление выполнено без остатка, считается, что в принятой комбинации ошибки не было, либо данной проверкой она не обнаружена. Наличие остатка является признаком ошибки и указывает на искажение кодовой комбинации.

На втором этапе осуществляется определение искаженного символа и его исправление. На этом этапе могут использоваться различные методы декодирования: оптимальные, стандартной расстановки, методы, основанные на выборе синдрома.

К оптимальным методам декодирования относятся методы декодирования по максимуму апостериорной вероятности (МАВ) и по максимуму правдоподобия (МП), минимизирующие среднюю вероятность ошибки

P p(Ui ) p(e /Ui ) .

ется по максимальному значению апостериорной вероятности p(U / ~ ), во вто-

i U j

ром – по максимуму функции правдоподобия p( ~ /U ). Решение принимается по

U j i

всем Ui C, где Ui - переданная кодовая комбинация, принадлежащая множеству

наименьшем числе символов в случае передачи кодовых комбинаций по двоичному симметричному каналу МП является частным случаем МАВ. Оба метода декодирования эквивалентны. Следует отметить, что декодирование, использующее метод стандартной расстановки, является декодированием по максимуму правдоподобия.

163

Реализация этих методов требует значительных ресурсов памяти декодера, равной по объёму числу кодовых комбинаций используемого кода. Поэтому оптимальные методы используются для исправления ошибок малой кратности при небольших параметрах (n,k) кодов.

Процесс декодирования может быть существенно упрощен при использовании методов синдромного декодирования, основанных на свойствах циклических кодов.

Рассмотрим более подробно метод синдромного декодирования кодовых комбинаций кода (7,4), исправляющего ошибки первой кратности и обнаруживающего ошибки первой и второй кратности, с помощью декодера Меггитта.

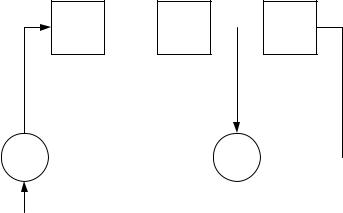
Основным элементом декодера является генератор синдромов (ГС), рис.20.3, который получается из схемы кодера систематического кода (рис.20.2) устранением ключа К.

S1 S2 S3

+ +

Е

Рис.20.3

В схеме декодера ГС выполняет две функции: деление принятой кодовой комбинации на производящий полином; формирование синдрома для исправления одиночной ошибки в любом разряде принятой кодовой комбинации.

Для определения синдрома выполняется деление ошибки вида E=0000001, в которой 1 означает ошибку в старшем разряде кодовой комбинации кода (7,4), на производящий полином. В таблице 20.4 отображен процесс деления генератором синдромов ошибки вида E=0000001. Состояние, в которое пришли триггеры на 8-м такте, означает наличие остатка и представляет собой синдром ошибки первой кратности.

Таблица 20.4

164

Структурная схема декодера Меггитта показана на рисунке 20.4.

Рис.20.4

Декодер работает следующим образом. Кодовая комбинация из 7 символов поступает в буферный регистр и одновременно в регистр генератора синдромов, где производится деление комбинации на производящий полином кода g(x) = x3 +x+1: семь тактов заполняется буферный регистр, семь тактов генератор синдромов делит кодовую комбинацию. Если ошибки в комбинации не было или

165

данной проверкой она не обнаружена, то состояние регистра генератора синдромов на 8-м такте будет нулевым (S1,S2,S3 = 000). При наличии ошибки состояние триггеров S1,S2,S3 будет отлично от нулевого и приведет к срабатыванию логического элемента ИЛИ, который подключается к выходам триггеров генератора синдромов ключом К2 на 8-м такте и обеспечивает фиксацию ошибки в кодовой комбинации. На 8-м такте также размыкается ключ К1 и символы комбинации поступают на выход схемы, а генератор синдромов осуществляет циклический сдвиг составляющих S1,S2,S3 до состояния 001, на которое настроен дешифратор - схема И. На выходе схемы И появляется 1, которая подается на вход сумматора; на второй вход которого поступает искаженный символ.

В таблице 20.5 приведено состояние триггеров S1,S2,S3 генератора синдромов при декодировании искаженной комбинации U= 1111011 (неискаженная комбинация U=1111111). Как видно из таблицы 20.5, на 10-м такте триггеры S1,S2,S3 приходят в состояние 001 и происходит исправление ошибки в третьем разряде кодовой комбинации.

166

Для исправления ошибок большой кратности используются как синдромные методы декодирования, так и субоптимальные методы декодирования, к которым относятся алгебраические методы: прямой, поэтапный, мажоритарный и перестановочные методы. Рассмотрим пример мажоритарного декодирования на примере циклического кода (7,3).

Мажоритарное декодирование циклических кодов. Этот метод основан на возможности составления системы проверок для каждого символа принятой кодовой комбинации. Для их формирования используется проверочная матрица H. Каждая i- я строка матрицы задаёт соотношение, связывающее между собой символы кодовой комбинации (a0, a1, a2, a3, …, an): hi0 a0 + hi1 a1 +…+ hi n-\ an-1 =0, i = 1, 2,3, … , n – k. Совокупность этих соотношений называется контрольными проверками. На их основе формируется система разделённых проверок, удовлетворяющая требованиям: проверяемый символ ai входит в каждую контрольную проверку; любой другой символ aj (j i) входит лишь в одну из проверок в противном случае оценки являются связанными.

Благодаря этим требованиям в системе разделённых проверок каждая ошибка в проверяемом символе ai искажает все проверки, а ошибка в символе aj (j i) искажает только одну проверку, что позволяет принимать решение о значении символа ai по большинству проверок. При использовании мажоритарного метода декодирования для исправления t ошибочных символов необходимо иметь (2 t +1) проверочных соотношений.

Для циклических кодов достаточно задать систему проверок одного из символов кодового слова. Эта же система проверок используется для исправления остальных символов после соответствующей циклической перестановки принятой кодовой комбинации.

На рисунке 20.5 приведена структурная схема мажоритарного декодера для циклического кода (7,3). Код задается порождающим полиномом g(x)=1+x2+x3+x4. По проверочному полиному h(x)=1+х+x3 можно построить матрицу H и систему разделённых проверок

Дополняя систему соотношением a1= a1, получаем разделённые проверки для символа a1 в виде

167

a1 a1,

a1 a2 a4 , (20.4) a1 a5 a6,

a1 a3 a7.

Декодер состоит из буферного регистра и мажоритарного элемента (М). В течение первых 7 тактов кодовая комбинация записывается в буферный регистр. На 8-м такте ключ размыкается, принимается решение о значении символа а1 по большинству проверок, исправленный первый символ считывается с выхода мажоритарного элемента, поступает на выход декодера и через ключ в седьмую ячейку регистра. В результате циклических сдвигов принятой кодовой комбинации в буферном регистре исправляются остальные символы. Таким образом, декодирование кодовой комбинации происходит за 14 тактов.

Мажоритарный метод является одним из наиболее простых методов декодирования, применяемый при декодировании циклических, свёрточных кодов, кодов Рида-Маллера и некоторых других.

КОНТРОЛЬНЫЕ ВОПРОСЫ:

1.Что означает свойство цикличности кода?

2.Дайте определение циклического (n,k) кода?

3.Какими свойствами должен обладать производящий полином циклического (n,k) кода?

4.Какие функции выполняет генератор синдромов в схеме декодера?

5.Какое количество уравнений надо составить при мажоритарном декодировании циклических кодов?

ЛЕКЦИЯ 21. СВЕРТОЧНЫЕ КОДЫ

Общие свойства и способы представления. Сверточные коды – это коды с большой избыточностью, характеризуются простотой реализации кодирующих устройств и наиболее пригодны для исправления пакетов ошибок. Сверточные коды являются разновидностью непрерывных кодов.

Кодовую последовательность таких кодов можно рассматривать как линейную свертку импульсной характеристики кодера с входной информационной по-

168

Скорость кода R=k0/n0 определяет избыточность кода, равную 1- R. Длина кодового слова n при данной скорости R определяется не только n0, но также длиной (или максимальной степенью) производящих многочленов

n n0 max deg gij (x) 1 , (21.2)

i, j

при этом информационная длина кодового слова

kk0 max deg gij (x) 1 ,

i, j

Вместо длины кодового слова часто используется понятие «длина кодового ограничения» nа, которая показывает максимальное расстояние между позициями информационных символов, участвующих в формировании проверочного символа данного кода (например, при R =1/2 длина кодового ограничения равна числу ячеек памяти регистра сдвига кодера)

k 0

nа = max [ deg gij (x)+1] .

i 1

Входная последовательность из k нформационных символов представляется вектором-строкой ,

D(x) = [di(x)] = [d1(x), d2(x), ...dk0(x)];

а кодовое слово на выходе кодера С(x) = [cj(х)] = [ c1(x) ... cn0(x)]. Операция кодирования представляется в виде произведения

С(х) = D(x) G(x)

или

k 0

cj(х) = di(x) gij(x).

i 1

Проверочная матрица H(x) должна удовлетворять условию

G(x) HT(x) = 0,

а вектор синдромов ошибки (синдромных полиномов) равен

S(x) = U(x) HT(x) = [Sj(х)] = [ S1(x) ... Sn0-k0(x)],

то есть (n0 - k0)-мерный вектор-строка из полиномов.

U(x) = C(x) + e(x)

где e(x) вектор ошибок в декодируемой последовательности U(x) .

Очевидно, что S(x) = U(x) HT(x) = e(x) HT(x).

Если свёрточный код является систематическим, то информационные символы на выходе кодера совпадают с информационной последовательностью на

170