- •«Санкт-Петербургский государственный электротехнический университет «лэти» им. В.И.Ульянова (Ленина)» (сПбГэту «лэти»)
- •Выпускная квалификационная работа бакалавра Тема: решение тропических линейных уравнений с трехдиагональными матрицами
- •Санкт-Петербургский государственный электротехнический университет
- •(СПбГэту “лэти”)
- •Задание на выпускную квалификационную работу
- •Реферат
- •Определения, обозначения и сокращения
- •Введение
- •1 Тропические системы линейных уравнений
- •Определение тропической математики
- •Тропические многочлены и матрицы
- •1.3 Решение тропической системы линейных уравнений
- •1.4 Описание алгоритма Григорьева
- •1.5 Пример работы алгоритма Григорьева
- •1.6 Тропические рекуррентные последовательности
- •2 Алгоритм гаусса и трёхдиагональные матрицы
- •2.1 Метод Гаусса-Жордана
- •2.2 Алгоритм Гаусса
- •2.3 Схема выбора главного элемента
- •Трёхдиагональные матрицы и метод прогонки
- •Сравнение алгоритмов гаусса и григорьева
- •3.1 Сравнение шагов алгоритма Гаусса и алгоритма Григорьева
- •3.2 Переупорядочивание строк и столбцов
- •Модификация алгоритма григорьева для трёхдиагональных матриц
- •4.1 Идеи модификации алгоритма Григорьева
- •4.2 Модификация программы
- •5 Экономическое обоснование
- •5.1 Обоснование целесообразности исследования
- •5.2 Трудоёмкость и календарный план
- •5.3 Оценка величины заработной платы и социальных отчислений участников исследования и разработки
- •5.4 Расчёт амортизации
- •5.5 Расчёт себестоимости разработки системы
- •Заключение
- •Список литературы
- •Приложение а
- •Приложение б
1 Тропические системы линейных уравнений
Тропическая математика – появившаяся сравнительно недавно область математики, при этом её развитие идёт очень активно. В связи с тем, что многие классические задачи сводятся к решению систем тропических линейных уравнений, так как имеют и классическую, и тропическую формулировки (и в этом смысле тропическая математика схожа с классической физикой, а классическая математика – с квантовой), она позволяет решать задачи, ответ на которые в классических терминах получать не удаётся.
Системы тропических линейных уравнений применяются при решении тропических дифференциальных уравнений и построении рекуррентных последовательностей, создании нейросетей с тропическими активационными функциями, в оптимизационных и экономических задачах. Доказано, что алгоритм Григорьева имеет неполиномиальную сложность, но на многих входных данных работает примерно за полиномиальное время. Отсюда и появляется задача построения специализации для узких классов матриц и поиска таких данных, на которых эффективность алгоритма выше, чем на остальных.
Определение тропической математики
Полукольцо
– это множество, над которым определены
операции сложения и умножения, причем
они оба ассоциативны ( ),
сложение коммутативно (
),
сложение коммутативно ( ),
а умножение дистрибутивно относительно
сложения (
),
а умножение дистрибутивно относительно
сложения ( – дистрибутивность слева и
– дистрибутивность слева и
 ).
).
Единица
полукольца – это
нейтральный по умножению элемент, т.е.
если
 – полукольцо, то 𝟙
– полукольцо, то 𝟙
 𝟙
𝟙 .
Нулём
называется
нейтральный по сложению элемент
полукольца:
.
Нулём
называется
нейтральный по сложению элемент
полукольца:
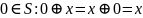 .
.
Если
сложение в полукольце идемпотентно
(т.е. повторное
применение операции даёт тот же результат,
что и первое применение:
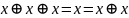 ),
то такая математика называется
идемпотентной
математикой.
),
то такая математика называется
идемпотентной
математикой.
Если
определить операцию сложения как
минимум:
 ,
а умножение – как сложение:
,
а умножение – как сложение:
 ,
то множество, над которым они определены,
будет называться тропическим
полукольцом. Тропическая математика
является
идемпотентной.
,
то множество, над которым они определены,
будет называться тропическим
полукольцом. Тропическая математика
является
идемпотентной.
Многие задачи имеют как классическую, так и тропическую формулировки. Переход от классической к тропической называется деквантованием (и в этом смысле тропическая математика схожа с классической физикой, а классическая математика – с квантовой), результатом применения деквантования Маслова [4]:
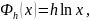
где
 ,
,
 - отображение из
- отображение из
 ,
так как если
,
так как если

то для сложения получим

а
тогда при
 (к нулю слева):
(к нулю слева):

Для умножения

В
качестве 𝟙
принимается
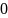 ,
так как
,
так как
 ,
что удовлетворяет определению нейтрального
по умножению элемента, а в качестве
принимается
,
что удовлетворяет определению нейтрального
по умножению элемента, а в качестве
принимается
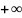 ,
так как
,
так как

Тропические многочлены и матрицы
Особенность
тропических многочленов заключается
в том, что все они по своей сути являются
линейными функциями. Например, моном
 при замене операций классической
математики тропическими, превратится
в
при замене операций классической
математики тропическими, превратится
в
 .
Рассмотрим, как такой результат был
получен:
.
Рассмотрим, как такой результат был
получен:

Чтобы избежать путаницы в обозначениях, тропическое возведение в степень будем обозначать со знаком тропического обозначения перед показателем.
Степень монома определяется как сумма степеней всех входящих в него переменных. Степень многочлена – это степень максимального монома в нём.
Так как многочлен представляет собой сумму мономов, а в тропическом смысле сумма – это минимум, тропический многочлен – это минимум из сумм переменных с их показателями:

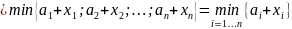
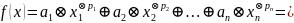

Таким образом, линейная функция классической математики превращается в формулу (1.1):
|
(1.1) |
а многочлен имеет вид

Тропический
многочлен задаёт кусочно-линейную
функцию. [5] Это свойство широко используется
в нейронных сетях: можно менять одну
часть функции, не затрагивая остальные.
Тропическая функция для полинома
непрерывна и вогнута, т.е.
 .
Построим график
.
Построим график :
при
:
при
 минимум будет достигаться на
минимум будет достигаться на
 ,
затем при
,
затем при
 – на
,
при
– на
,
при
 – на
– на
 ,
а дальше минимум будет равен пяти.
Покажем это на рисунке 1.1.
,
а дальше минимум будет равен пяти.
Покажем это на рисунке 1.1.
На рисунке 1.1 видно корни многочлена – это точки излома. В них минимум достигается хотя бы на двух мономах – это и есть определение корня. Объяснение этому берёт истоки от функции Иенсена [6].
 Рисунок
1.1 – График функции
Рисунок
1.1 – График функции 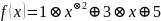
В тропической математике есть несколько определений невырожденности. Одно из них определено в терминах перманента. В классический математике перманент матрицы – это число, которое задаётся формулой
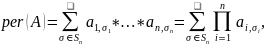
где
 – это множество всех возможных чисел
от 1 до n.
Иначе говоря, для матрицы из трёх
элементов перманент находится следующим
образом:
– это множество всех возможных чисел
от 1 до n.
Иначе говоря, для матрицы из трёх
элементов перманент находится следующим
образом:


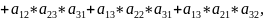
то есть перестановки определяют номера столбцов для соответствующих строк. Отметим, что перманент – это тот же определитель матрицы, только без учета чётности перестановок (чётность перестановки – это число инверсий элементов по модулю два: если естественный порядок двух соседних чисел нарушается четное число раз, то перестановка чётная, и наоборот для нечётной), влияющей на знаки слагаемых.
Теперь заменим классические операции тропическими и получим формулу тропического перманента
|
(1.2) |
или, в переходе к привычным обозначениям,
|
(1.3) |
Матрица называется тропически невырожденной (в терминах перманента), если на тропических суммах минимум достигается больше одного раза. Данное определение пригодится в дальнейшем – в разборе алгоритма Григорьева и способов его оптимизации для трёхдиагональных матриц.
Для квадратной матрицы перманент использует перестановки, а для прямоугольной – размещения номеров столбцов по номерам строк. Если же строк больше, чем столбцов, то считают перманент транспонированной матрицы. Он равен перманенту исходной.
Определений тропического ранга, как и определений невырожденности, несколько. Одним из них является размер её наибольшей тропически невырожденной подматрицы.