
Лабораторные / Лаба1
.docxФГБОУ ВО
«Уфимский государственный авиационный технический университет»
Лабораторная работа №1
по вычислительной математике
МЕТОД ГРАДИЕНТНОГО СПУСКА
Вариант №1
Выполнил: студент гр. ИВТ-
Проверила:
Шерыхалина Н. И.
Уфа 2022
1 Цель работы
Ознакомление с методами поиска экстремума нелинейной выпуклой функции нескольких переменных и решение таких задач с помощью ЭВМ.
2 Описание метода
Задача состоит в отыскании минимума функции двух переменных f(x,y) (следует отметить, что если необходимо найти максимум некоторой функции F(x,y), то эта задача сводится к поиску минимума функции f(x,y)=F(x,y) ).
Большинство численных методов состоит в отыскании некоторой последовательности (x0,y0), (x1,y1),..,(xk,yk), которая при k®®¥R (или при k®®kM) сходится к точке минимума (x*,y*). Если при этом выполняется f(x0,y0)>f(x1,y1)>..>f(xk,yk), то есть значения функции монотонно убывают при увеличении k, то такой метод называется методом спуска.
Известно, что вектор градиента функции

направлен в сторону наибольшего возрастания функции f(x,y). Поэтому в качестве направления движения можно принять противоположное градиенту направление (антиградиент), т.е. координаты точек пересчитываются по формулам
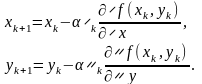 (5.1)
(5.1)
Выбор величины aak, с которой связана длина k-го шага, в общем случае является сложной задачей. Если k мало, то движение будет слишком медленным и потребует значительного объема вычислений. Если aak велико, то существует возможность перескочить точку минимума и выйти на противоположный склон функции. При этом возможно нарушение требования монотонного убывания последовательности f(xk,yk) и появляется опасность зацикливания, то есть колебания последовательности (xk,yk) в некоторой окрестности точки минимума (x*,y*) без приближения к ней.
Существует несколько различных способов выбора aak. В данной работе рассматривается разновидность метода с дроблением шага. Для этого задается начальное приближение (x0,y0) и начальное значение aa0 (например, x0=y0=0, 0=1). Вычисление x1,y1 и всех последующих xk+1,yk+1 производится по формуле (5.1). При этом если окажется, что f(xk+1,yk+1)>f(xk,yk), то величина k уменьшается в два раза и вычисление xk+1,yk+1 повторяется от точки (xk,yk) с новым значением k. Если же значение функции убывает, то величина k=k1.
Критерием окончания счета принимается неравенство
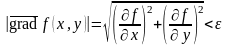 (5.2)
(5.2)
либо одновременное выполнение двух неравенств
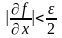 ,
,
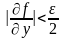 (5.3)
(5.3)
3 Выполнение работы
Составим
программу для формулы:
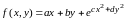 ,
где
,
где
a |
b |
c |
d |
1 |
-1.4 |
0.01 |
0.11 |
Листинг программы:
import numpy as np import math a = 1 b = -1.4 c = 0.01 d = 0.11 xx = 0 #начальное значение yy = 0 #начальное значение lmd = 1#шаг сходимости def f(x, y): #main func return a*x + b*y + math.exp(c*x*x + d*y*y) def dfx(x, y): #производная по x return a + 2*c*x*math.exp(c*x*x + d*y*y) def dfy(x, y): #производная по y return b + 2*d*y*math.exp(c*x*x + d*y*y) n = 0 fl = 1 # вывод таблицы print("№:\tx\ty\tf(x,y)\tdf/dx\tdf\dy") print(n, ":\t", round(xx, 5), "\t", round(yy, 5), "\t", round(f(xx, yy), 5), "\t", round(dfx(xx, yy), 5), "\t", round(dfy(xx, yy), 5)) while fl: n += 1 #счетчик if abs(dfx(xx, yy)) > 0.00005: xx = xx - lmd*dfx(xx, yy) if abs(dfy(xx, yy)) > 0.00005: yy = yy - lmd*dfy(xx, yy) # вывод таблицы print(n, ":\t", round(xx, 5), "\t", round(yy, 5), "\t", round(f(xx, yy), 5), "\t", round(dfx(xx, yy), 7), "\t", round(dfy(xx, yy), 7)) if (abs(dfx(xx, yy)) < 0.00005) & (abs(dfy(xx, yy)) < 0.00005): fl = 0
Составим таблицу преобразований:
№ |
x |
y |
f(x, y) |
df/dx |
df/dy |
0 |
0,00000 |
0,00000 |
1.0 |
1.0 |
-1.4 |
1 |
-1.0 |
1.4 |
-1.70693 |
0.9749385 |
-1.0140531 |
2 |
-1.97494 |
2.4027 |
-3.37659 |
0.9224985 |
-0.3628349 |
3 |
-2.89744 |
2.71785 |
-4.25144 |
0.8579687 |
0.0655071 |
4 |
-3.75541 |
2.56626 |
-4.97208 |
0.8215365 |
-0.058516 |
5 |
-4.57694 |
2.52973 |
-5.6257 |
0.7718061 |
-0.0126208 |
6 |
-5.34875 |
2.43189 |
-6.202 |
0.7270645 |
-0.0349631 |
7 |
-6.07581 |
2.34863 |
-6.71028 |
0.6775438 |
-0.0288885 |
8 |
-6.75336 |
2.253 |
-7.14974 |
0.6275098 |
-0.0330621 |
9 |
-7.38087 |
2.15928 |
-7.52427 |
0.5749229 |
-0.0320737 |
10 |
-7.95579 |
2.06526 |
-7.83659 |
0.5209702 |
-0.0321215 |
11 |
-8.47676 |
1.97512 |
-8.09107 |
0.4658173 |
-0.0308621 |
12 |
-8.94258 |
1.89026 |
-8.29285 |
0.4104898 |
-0.0292984 |
13 |
-9.35307 |
1.81265 |
-8.44818 |
0.356023 |
-0.0271486 |
14 |
-9.70909 |
1.7434 |
-8.56397 |
0.3036888 |
-0.0246478 |
15 |
-10.01278 |
1.68315 |
-8.64747 |
0.2547032 |
-0.0218667 |
16 |
-10.26748 |
1.63196 |
-8.70569 |
0.2101134 |
-0.0189675 |
17 |
-10.4776 |
1.5894 |
-8.74498 |
0.1706406 |
-0.0160898 |
18 |
-10.64824 |
1.55469 |
-8.77071 |
0.136621 |
-0.0133675 |
19 |
-10.78486 |
1.52686 |
-8.7871 |
0.1080154 |
-0.0108978 |
20 |
-10.89287 |
1.50485 |
-8.79729 |
0.0844829 |
-0.008739 |
21 |
-10.97735 |
1.48764 |
-8.80349 |
0.0654848 |
-0.0069103 |
22 |
-11.04284 |
1.47432 |
-8.8072 |
0.050387 |
-0.0054015 |
23 |
-11.09323 |
1.46408 |
-8.8094 |
0.0385421 |
-0.0041827 |
24 |
-11.13177 |
1.45625 |
-8.81068 |
0.0293448 |
-0.0032149 |
25 |
-11.16111 |
1.4503 |
-8.81142 |
0.0222611 |
-0.0024567 |
26 |
-11.18337 |
1.44579 |
-8.81184 |
0.01684 |
-0.0018687 |
27 |
-11.20021 |
1.44237 |
-8.81209 |
0.0127116 |
-0.0014166 |
28 |
-11.21293 |
1.4398 |
-8.81222 |
0.0095795 |
-0.001071 |
29 |
-11.22251 |
1.43786 |
-8.8123 |
0.0072102 |
-0.000808 |
30 |
-11.22972 |
1.4364 |
-8.81235 |
0.0054217 |
-0.0006087 |
31 |
-11.23514 |
1.43531 |
-8.81237 |
0.0040739 |
-0.000458 |
32 |
-11.23921 |
1.43448 |
-8.81239 |
0.0030595 |
-0.0003443 |
33 |
-11.24227 |
1.43386 |
-8.8124 |
0.0022968 |
-0.0002587 |
34 |
-11.24457 |
1.4334 |
-8.8124 |
0.0017237 |
-0.0001942 |
35 |
-11.24629 |
1.43305 |
-8.8124 |
0.0012933 |
-0.0001458 |
36 |
-11.24758 |
1.43279 |
-8.8124 |
0.0009702 |
-0.0001094 |
37 |
-11.24856 |
1.43259 |
-8.8124 |
0.0007277 |
-8.21e-05 |
38 |
-11.24928 |
1.43245 |
-8.8124 |
0.0005458 |
-6.16e-05 |
39 |
-11.24983 |
1.43234 |
-8.81241 |
0.0004093 |
-4.62e-05 |
40 |
-11.25024 |
1.43225 |
-8.81241 |
0.0003069 |
-3.46e-05 |
41 |
-11.25054 |
1.43219 |
-8.81241 |
0.0002302 |
-2.6e-05 |
42 |
-11.25077 |
1.43219 |
-8.81241 |
0.0001579 |
4.65e-05 |
43 |
-11.25093 |
1.43209 |
-8.81241 |
0.0001387 |
-4.03e-05 |
44 |
-11.25107 |
1.43209 |
-8.81241 |
9.52e-05 |
3.4e-06 |
45 |
-11.25117 |
1.43209 |
-8.81241 |
6.53e-05 |
3.34e-05 |
46 |
-11.25123 |
1.43204 |
-8.81241 |
6.18e-05 |
-2.26e-05 |
47 |
-11.25129 |
1.43204 |
-8.81241 |
4.24e-05 |
-3.1e-06 |
Вывод: был изучен метод поиска экстремума нелинейной выпуклой функции нескольких переменных и приобретены навыки решение подобных задач с помощью ЭВМ.
