Лабораторные / Лабораторная работа №5_Моделирование_Гвоздев

ФГБОУ ВО

«Уфимский государственный авиационный технический университет»

Кафедра ТК

ОТЧЕТ

по лабораторной работе № 4

по дисциплине «Моделирование»

Специальные статистические методы обработки малого числа выборочных данных

Вариант – 18

Выполнил: студент гр.

Проверил:

Гвоздев В.Е.

Уфа 2022

Задача: на основе выборочных данных, построить оценки законов распределения наработки до отказа приведенными методами (последовательных медиан, уменьшения неопределенности, сжатия ИЗР). Составить полученные оценки на основе приведенных метрик ( , , ).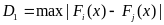

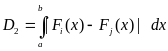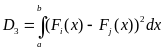Ход работы:

Выборочные данные: 18,0398814136346, 18,0715705458537, 18,0931646863426, 18,1364386662509, 18,2213123435287, 18,2435467998024, 18,2839362034136, 18,4119105128262, 18,4125823116777, 18,5340015928788, 18,5858939225152, 18,586086640399, 18,5869889564953, 18,6656550435988, 18,8416850088926, 18,8787734250137, 18,8895976702967, 18,9839233717436, 19,0212891028320, 19,1064554162363, 19,1251115261998, 19,2089391781662, 19,2400204092315, 19,3297756275043, 19,4538156389978, 19,4867300820571, 19,6246528750553, 19,6994660814548, 19,7769380645909, 19,7867618367424.

Метод последовательных медиан

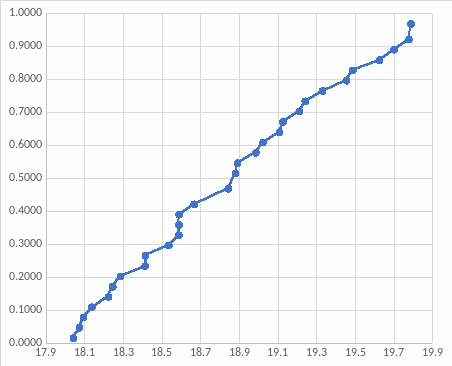
xi	F(xi)
18,0	0,0156
18,1	0,0469
18,1	0,0781
18,1	0,1094
18,2	0,1406
18,2	0,1719
18,3	0,2031
18,4	0,2344
18,4	0,2656
18,5	0,2969
18,6	0,3281
18,6	0,3594
18,6	0,3906
18,7	0,4219
18,8	0,4688
18,9	0,5156
18,9	0,5469
19,0	0,5781
19,0	0,6094
19,1	0,6406
19,1	0,6719
19,2	0,7031
19,2	0,7344
19,3	0,7656
19,5	0,7969
19,5	0,8281
19,6	0,8594
19,7	0,8906
19,8	0,9219
19,8	0,9688

Метод уменьшения неопределенности

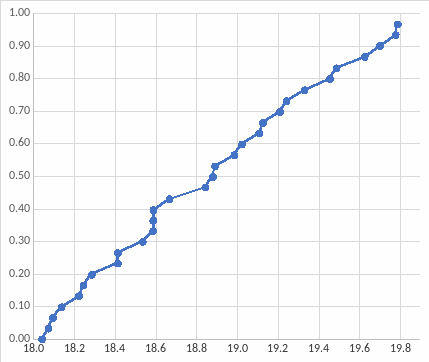
№	xi	F(xi), F(x)
1	18,0	0,00
2	18,1	0,03
3	18,1	0,07
4	18,1	0,10
5	18,2	0,13
6	18,2	0,16
7	18,3	0,20
8	18,4	0,23
9	18,4	0,26
10	18,5	0,30
11	18,6	0,33
12	18,6	0,36
13	18,6	0,40
14	18,7	0,43
15	18,8	0,47
16	18,9	0,50
17	18,9	0,53
18	19,0	0,57
19	19,0	0,60
20	19,1	0,63
21	19,1	0,66
22	19,2	0,70
23	19,2	0,73
24	19,3	0,77
25	19,5	0,80
26	19,5	0,83
27	19,6	0,87
28	19,7	0,90
29	19,8	0,93
30	19,8	0,97

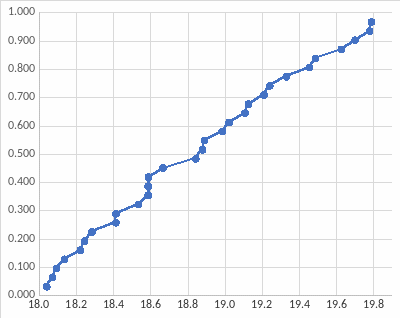Метод сжатия интегральных законов распределения

№	xi	ai
1	18,0	0,032
2	18,1	0,065
3	18,1	0,097
4	18,1	0,129
5	18,2	0,161
6	18,2	0,194
7	18,3	0,226
8	18,4	0,258
9	18,4	0,290
10	18,5	0,323
11	18,6	0,355
12	18,6	0,387
13	18,6	0,419
14	18,7	0,452
15	18,8	0,484
16	18,9	0,516
17	18,9	0,548
18	19,0	0,581
19	19,0	0,613
20	19,1	0,645
21	19,1	0,677
22	19,2	0,710
23	19,2	0,742
24	19,3	0,774
25	19,5	0,806
26	19,5	0,839
27	19,6	0,871
28	19,7	0,903
29	19,8	0,935
30	19,8	0,968

Сопоставление результатов:

	1	2	3
1	0	0,419	0,420
2	0,419	0	0,032
3	0,420	0,032	0

	1	2	3
1	0	4,6140	5,0020
2	4,6140	0	0,4224
3	5,0020	0,4224	0

	1	2	3
1	0	0,0847	0,0918
2	0,0847	0	0,0016
3	0,0918	0,0016	0

Контрольные вопросы

1. В чем заключается основная идея метода прямоугольных вкладов?

Метод основан на использовании априорной информации о неизвестном распределении и учете случайного характера выбора. Априорная информация о распределении состоит в следующем: при известных границах [a, b] интервала, на котором определена случайная величина X, плотность распределения удовлетворяет условию: f (x) 0  x  [a, b], f (x) 0  x  [a, b]; плотность распределения непрерывна внутри интервала [a, b] и не имеет очень крутых подъемов и спадов.

2. Условия применимости метода прямоугольных вкладов.

1.

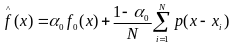
где а 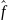(x) – эмпирическая компонента;

f₀ (x) – априорная компонента;

p(x - x_i)  составляющая эмпирической компоненты, связанная с i-й реализацией выборки;

0 – вес априорной компоненты.

2. Плотность распределения должна удовлетворять условию: f (x) 0  x  [a, b], f (x) 0  x  [a, b];

3. В чем отличие метода уменьшения неопределенности от метода прямоугольных вкладов?

Отличие заключается в том, что вместо прямоугольного вклада ширины d, построенного около реализации x_i, применяется нормированное равномерное распределение, заданное на интервале [x_i-1, x_i+1].

4. Почему в качестве априорной компоненты метода прямоугольных вкладов целесообразно использовать равномерное распределение?

Причина, по которой в качестве априорной компоненты метода прямоугольных вкладов целесообразно использовать равномерное распределение состоит в том, что плотность распределения должна быть непрерывна и не иметь крутых подъемов и спадов.

5. Преимущества и недостатки метода сжатия области существования интегральных законов распределения?

Преимущества:

- возможность вычислить доверительную вероятность для каждого i-го члена последовательности;

- обеспечивает высокую точность оценивания функции распределения в окрестности узлов интерполяции.

Недостатки:

- точность воспроизведения вне окрестности узлов интерполяции при малом числе наблюдений невысока.