
An Introduction to Statistical Signal Processing
.pdfA.5. LINEAR SYSTEM FUNDAMENTALS |
405 |
with equality if and only if the eigenvalues are all constant.
A square Hermitian matrix A can be diagonalized into the form
A = UΛU , |
(A.30) |
where Λ is the diagonal matrix with diagonal entries Λ(k, k) = λk, the
kth eigenvalue of the matrix, and where U is a unitary matrix, that is,
U = U−1.
The inner product and outer product of two vectors can be related as
xty = Tr(xyt). |
(A.31) |
Given an n-dimensional vector x and an n by n matrix A, the product
|
n−1 n−1 |
xtAx = |
|
xkxjak,j |
|
|
k=0 j=0 |
is called a quadratic form. If the matrix A is such that xtAx ≥ 0, the matrix is said to be nonnegative definite. If the matrix is such that xtAx > 0, then the matrix is said to be positive definite. These are the definitions for real-valued vectors and matrices. For complex vectors and matrices use the conjugate transpose instead of the transpose. If a matrix is positive definite, then its eigenvalues are all strictly positive and hence so is its determinant.
A quadratic form can also be written as
xtAx = Tr(Axxt). |
(A.32) |
If a matrix is A positive definite and Hermitian (e.g., real and symmet-
ric), then its square root A1/2 is well-defined as UΛ1/2U . In particular,
A1/2A1/2 = A and (A1/2)−1 = (A−1)1/2.
A.5 Linear System Fundamentals
In general, a system L is a mapping of an input time function or input signal, x = {x(t); t T } into an output time function or output signal, L(x) = y = {y(t); t T }. We now use T to denote the index set or domain of definition instead of I to emphasize that the members of the set correspond to “time.” Usually the functions take on real or complex values of each value of time t in T . The system is called a discrete time system if
Tis discrete; e.g., Z or Z+, and it is called a continuous time system if T is continuous; e.g., or [0, ∞). If only nonnegative times are allowed, e.g.,
Tis Z+ or [0, ∞), the system is called a one-sided or single-sided system. If
406 |
APPENDIX A. PRELIMINARIES |
time can go on infinitely in both directions, then it is said to be a two-sided system.
A system L is said to be linear if the mapping is linear, that is, for all complex (or real) constants a and b and all input functions x1 and x2
L(ax1 + bx2) = aL(x1) + bL(x2) . |
(A.21) |
There are many ways to define or describe a particular linear system: one can provide a constructive rule for determining the output from the input; e.g., the output may be a weighted sum or integral of values of the input. Alternatively, one may provide a set of equations whose solution determines the output from the input, e.g., di erential or di erence equations involving the input and output at various times. Our emphasis will be on the former constructive technique, but we shall occasionally consider examples of other techniques.
The most common and the most useful class of linear systems comprises systems that can be represented by a convolution, that is, where the output is described by a weighted integral or sum of input values. We first consider continuous time systems and then turn to discrete time systems.
For t T , let x(t) be a continuous time input to a system with output y(t) defined by the superposition integral
y(t) = |
x(t − s)ht(s) ds . |
(A.22) |
|
s:t−s T |
|
The function ht(t) is called the impulse response of the system since it can be considered the output of the system at time t which results from an input of a unit impulse of Dirac delta function x(t) = δ(t) at time 0. The index set is usually either (−∞, ∞) or [0, ∞) for continuous time systems. The linearity of integration implies that the system defined by (A.22) is a linear system. A system of this type is called a linear filter. If the impulse response does not depend on time t, then the filter is said to be time-invariant and the superposition integral becomes a convolution integral:
y(t) = s:t−s T x(t − s)h(s) ds = s T x(s)h(t − s) ds . |
(A.23) |
We shall deal almost exclusively with time-invariant filters. Such a linear time-invariant system is often depicted using a block diagram as in Figure A.3.
If x(t) and h(t) are absolutely integrable, i.e.,
|x(t)|dt , |
|h(t)|dt < ∞ , |
(A.24) |
TT
A.5. LINEAR SYSTEM FUNDAMENTALS |
|
|
|
|
|
|
407 |
||||||||||||||||||
x(t) |
|
|
|
|
|
|
|
|
|
|
|
|
y(t) = s T x(s)h(t − s) ds |
||||||||||||
|
|
|
|
h |
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Figure A.3: Linear Filter |
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
H |
(f) |
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
y(t) |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
x(t) |
|
|
|
|
|
h1 |
|
|
|
|
h2 |
|
|
|
z(t) |
||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X(f) |
|
|
|
|
H1 |
(f) Y (f) H2(f) |
|
Z(f) |
|||||||||||||||||
Figure A.4: Cascade Filter |
|
|
|
|
|
|
|
|
|||||||||||||||||
then their Fourier transforms exist: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
X(f) = T x(t)e−j2πftdt , |
|
H(f) = T h(t)e−j2πftdt . |
|
(A.25) |
|||||||||||||||||||||
Continuous time filters satisfying (A.24) are said to be stable. H(f) is called the filter transfer function or the system function. We point out that (A.24) is a su cient but not necessary condition for the existence of the transform. We shall not usually be concerned with the fine points of the existence of such transforms and their inverses. The inverse transforms that we require will be accomplished either by inspection or by reference to a table.
A basic property of Fourier transforms is that convolution in the time domain corresponds to multiplication in the frequency domain, and hence the output transform is given by
Y (f) = H(f)X(f) . |
(A.26) |
Even if a particular system has an input that does not have a Fourier transform, (A.26) can be used to find the transfer function of the system by using some other input that does have a Fourier transform.
As an example, consider Figure A.4, where two linear filters are concatenated or cascaded: x(t) is input to the first filter, and the output y(t) is input to the second filter, with final output z(t). If both filters are stable and x(t) is absolutely integrable, the Fourier transforms satisfy
Y (f) = H1(f)X(f) , Z(f) = H2(f)Y (f) , |
(A.27) |
408 |
APPENDIX A. PRELIMINARIES |
or
Z(f) = H2(f)H1(f)X(f) .
Obviously the overall filter transfer function is H(f) = H2(f)H1(f). The overall impulse response is then the inverse transform of H(f).
Frequently (but not necessarily) the output of a linear filter can also be represented by a finite order di erential equation in terms of the di erential operator, D = d/dt :
n |
m |
|
|
|
|
akDky(t) = |
biDix(t) . |
(A.28) |
k=0 |
i=0 |
|
The output is completely specified by the input, the di erential equation, and appropriate initial conditions. Under suitable conditions on the differential equation, the linear filter is stable, and the transfer function can be obtained by transforming both sides of (A.28). However, we shall not pursue this approach further.
Turn now to Figure A.5. Here we show an idealized sampled data system to demonstrate the relationship between discrete and continuous time
filters. The input function x(t) is input to a mixer, which forms the product
of x(t) with a pulse train, p(t) = k T δ(t − k), of Dirac delta functions spaced one second apart in time. T is a suitable subset of Z. If we denote the sampled values x(k) by xk, the product is
x(t)p(t) = xkδ(t − k),
k
which is the input to a linear filter with impulse response h(t). Applying the convolution integral of equation (A.23) and sampling the output with a switch at one-second intervals, we have as an output function at time n
yn = |
y(n) |
|
|
|
|
= |
x(t)p(t)h(t − n) dt |
|
= |
xkδ(t − k)h(t − n) dt |
|
= |
k xkhn−k |
|
|
k:k T |
|
= |
|
(A.29) |
xn−khk . |
k:n−k T
Thus, macroscopically the filter is a discrete time linear filter with a discrete convolution sum in place of an integral. {hk} is called the Kronecker δ response of the discrete time filter. Its name is derived from the
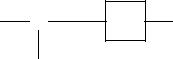
A.5. LINEAR SYSTEM FUNDAMENTALS |
409 |
x(t)p(t)
x(t) × h y(t)
p(t) = k T δ(t − k)
Figure A.5: Sampled Data System
fact that hk is the output of the linear filter at time k when a Kronecker delta function is input at time zero. It is also sometimes referred to as the “discrete time impulse response” or the “unit pulse response.” If only a finite number of the hk are nonzero, then the filter is sometimes referred to as an FIR (finite impulse response) filter. If a filter is not an FIR filter, then it is an IIR (infinite impulse response) filter.
If {hk} and {xk} are both absolutely summable,
|hk| < ∞ , |
|xk| < ∞ , |
(A.30) |
k |
k |
|
then their discrete Fourier transforms exist:
H(f) = |
hke−j2πkf , X(f) = xke−j2πkf . |
(A.31) |
k |
k |
|
Discrete time filters satisfying (A.30) are said to be stable. H(f) is called the filter transfer function. The output transform is given by
Y (f) = H(f)X(f) . |
(A.32) |
The example of Figure A.4 applies for discrete time as well as continuous time.
For convenience and brevity, we shall occasionally use a general notation F to denote both the discrete and continuous Fourier transforms; that is,
F |
(x) = |
T x(t)e−j2πftdt , |
T continuous, |
(A.33) |
||
|
|
xke−j2πfk , |
|
discrete, |
|
|
|
|
|
|
T |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
k T
A more general discrete time linear system is described by a di erence equation of the form
akyn−k = |
bixn−k . |
(A.34) |
ki
410 |
APPENDIX A. PRELIMINARIES |
Observe that the convolution of (A.29) is a special case of the above where only one of the ak is not zero. Observe also that the di erence equation (A.34) is a discrete time analog of the di erential equation (A.28). As in that case, to describe an output completely one has to specify initial conditions.
A continuous time or discrete time filter is said to be causal if the pulse response or impulse response is zero for negative time; that is, if a discrete time pulse response hk satisfies hk = 0 for k < 0 or a continuous time impulse response h(t) satisfies h(t) = 0 for t < 0.
A.6 Problems
1.Use the first seven relations to prove relations (A.10), (A.13), and (A.16).
2.Use relation (A.16) to obtain a partition {Gi; i = 1, 2, . . . , k} of Ω from an arbitrary finite class of collectively exhaustive sets {Fi; i = 1, 2, . . . , k} with the property that Gi Fi for all i and
i |
i |
|
j |
Gj = |
Fj all i . |
j=1 |
=1 |
Repeat for a countable collection of sets {Fi}. (You must prove that the given collection of sets is indeed a partition.)
3. If {Fi} partitions Ω, show that {G ∩ Fi} partitions G.
4. Show that F G implies that F ∩ G = F, F G = G, and Gc F c.
5.Show that if F and G are disjoint, then F Gc.
6.Show that F ∩ G = (F G) − (F ∆G).
7. Let Fr = [0, 1/r), r (0, 1]. Find |
|
Fr and |
r |
|
Fr. |
||
r (0,1] |
|
(0,1] |
|
8.Prove the countably infinite version of DeMorgan’s “laws.” For example, given a sequence of sets Fi; i = 1, 2, . . . , then
∞ |
Fi = |
∞ |
Fic c . |
|
|
i |
|
i=1 |
|
=1 |
|
A.6. PROBLEMS |
|
|
411 |
9. Define the subsets of the real line |
|
|
|
Fn = r : |r| |
> |
1 |
, |
|
|||
n |
|||
and |
|
|
|
F = {0} . |
|
|
|
Show that |
|
|
|
∞ |
|
|
|
n |
|
|
|
F c = |
Fn . |
|
|
=1 |
|
|
|
10.Let Fi, i = 1, 2, . . . be a countable sequence of “nested” closed intervals whose length is not zero, but tends to zero; i.e., for every i,
Fi = [ai, bi] Fi−1 Fi−2 . . . and bi − ai → 0 and i → ∞. What are
|
∞ |
the points in |
i |
Fi? |
|
|
=1 |
11.Prove that the interval [0, 1] cannot be put into one-to-one correspondence with the set of integers as follows: Suppose that there is such
a correspondence so that x1, x2, x3, · · · is a listing of all numbers in [0, 1]. Use Problem 10 to construct a set that consists of a point not in this listing. This contradiction proves the statement.
12.Show that inverse images preserve set theoretic operations, that is, given f : Ω → A and sets F and G in A, then
f−1(F c) = (f−1(F ))c .
f−1(F G) = f−1(F ) f−1(G) ,
and
f−1(F ∩ G) = f−1(F ) ∩ f−1(G) .
If {Fi, i I} is an indexed family of subsets of A that partitions A, show that {f−1(Fi); i I} is a partition of Ω. Do images preserve set theoretic operations in general? (Prove that they do or provide a counterexample.)
13.An experiment consists of rolling two four-sided dice (each having faces labeled 1, 2, 3, 4) on a glass table. Depict the space Ω of possible outcomes. Define two functions on Ω: X1(ω) = the sum of the two down faces and X2(ω) = the product of the two down faces. Let A1 denote the range space of X1, A2 the range space of X2, and A12 the range space of the vector-valued function X = (X1, X2),
412 |
APPENDIX A. PRELIMINARIES |
that is, X(ω) = (X1(ω), X2(ω)). Draw in both Ω and A12 the set
2
{ω : X1(ω) < X2(ω)}. The cartesian product Ai of two sets is
i=1
defined as the collection of all pairs of elements, one from each set,
that is
2
Ai = {all a, b : a A1, b A2} .
i=1
2
Is it true above that A12 = Ai?
i=1
14.Let Ω = [0, 1] and A be the set of all infinite binary vectors. Find a one-to-one mapping from Ω to A, being careful to note that some rational numbers have two infinite binary representations (e.g., 1/2 =
.1000 . . . = .0111 . . . in binary).
15.Can you find a one-to-one mapping from:
(a)[0, 1] to [0, 2)?
(b)[0, 1] to the unit square in two-dimensional Euclidean space.
(c)Z to Z+? When is it possible to find a one-to-one mapping from one space to another?
16.Suppose that a voltage is measured that takes values in Ω = [0, 15]. The voltage is mapped into the finite space A = {0, 1, · · · , 15} for transmission over a digital channel. A mapping of this type is called a quantizer. What is the best mapping in the sense that the maximum error is minimized?
17.Let A be as in Problem 16, i.e., the space of 16 messages which is mapped into the space of 16 waveforms, B = {cos nt, n = 0, 1, · · · , 15; t [0, 2π]}. The selected waveform from B is transmitted on a waveform channel, which adds noise; i.e., B is mapped into C = {set of all possible waveforms {y(t) = cos nt + noise(t); t [0, 2π]}}. (This is a random mapping in a sense that will be described in subsequent chapters.) Find a good mapping from C into D = A. D is the decision space and the mapping is called a decision rule. (In other words, how would you perform this mapping knowing little of probability theory. Your mapping should at least give the correct decision if the noise is absent or small.)
18.Given a continuous time linear filter with impulse response h(t) given by e−at for ≥ 0 and 0 for t < 0, where a is a positive constant, find

A.6. PROBLEMS |
413 |
the transfer function H(f) of the filter. Is the filter stable? What happens if a = 0?
19.Given a discrete time linear filter with pulse response hk given by rk for k ≥ 0 and 0 for k < 0, where r has magnitude strictly less than 1, find the transfer function H(f). (Hint: Use the geometric series formula.) Is the filter stable? What happens if r = 1? Assume that |r| < 1. Suppose that the input xk = 1 for all nonnegative k and xk = 0 for all negative k is put into the filter. Find a simple expression for the output as a function of time. Does the transform of the output exist?
20.A continuous time system is described by the following relation: Given an input x = {x(t); t } is defined for each t by
y(t) = (a0 + a1x(t)) cos(2πf0t + θ) ,
where a0, a1, f0, and θ are fixed parameters. (This system is called an amplitude modulation (AM) system.) Under what conditions on the parameters is this system linear? Is it time-invariant?
21.Suppose that x = {x(t); t R}, where R = (−∞, ∞) is the real line, is a continuous time signal defined by
x(t) = 1 |t| ≤ T
0 otherwise,
where T > 0 is a fixed parameter, is put into a linear, time-invariant (LTI) filter described by an impulse response h = {h(t); t R}, where
t ≥ 0
h(t) =
0otherwise.
(a)Find the Fourier transform X of x, i.e.,
∞
X(f) = x(t)e−j2πft dt; f R,
−∞
√
where j = −1. Find the Fourier transform H of h.
(b)Find y, the output signal of the LTI filter, and its Fourier transform Y .

