
text_lab4
.pdf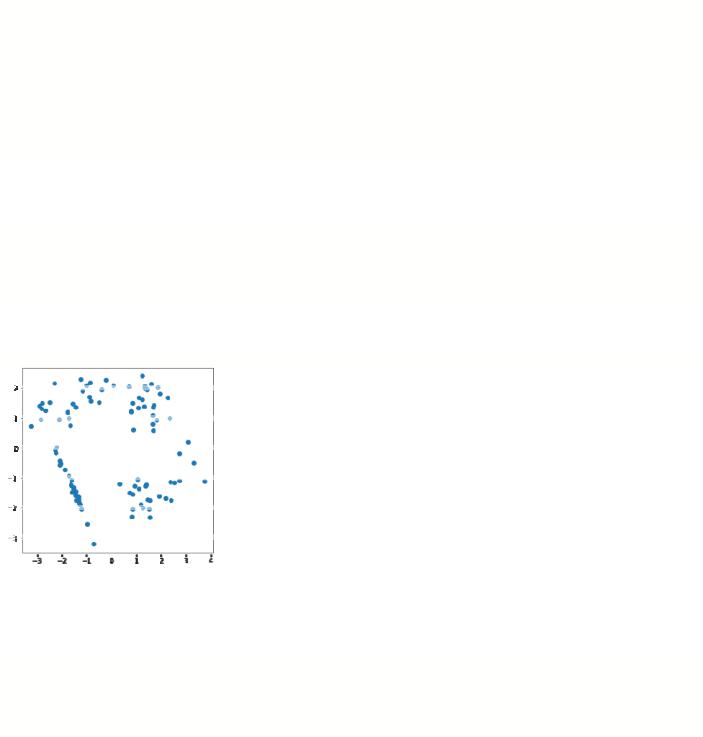
Отчет по лабораторной работе № 4
по дисциплине «Основы анализа текстовых данных»
на тему: «Кластеризация данных»
Цель работы:
Получить практические навыки решения задачи кластеризации фактографических данных в среде Jupiter Notebook (Эта лабораторная выполнялась в среде Google Colab). Научиться настраивать параметры методов и оценивать точность полученного разбиения.
1. Загрузим выборки согласно варианту задания.
Импортируем необходимые библиотеки:
from sklearn.metrics.pairwise import euclidean_distances from sklearn.cluster import KMeans
from scipy.cluster.hierarchy import linkage, dendrogram, fcluster import matplotlib.pyplot as plt
import numpy as np
from sklearn.datasets import make_classification import math as math
Загрузим выборки:
X, y = make_classification(random_state = 5, class_sep = 1.5, n_samples = 100, n_features = 2, n_redundant = 0, n_informative = 2, n_clusters_per_class = 1, n_classes = 4)
2. Отобразим данные на графике в пространстве признаков.
plt.scatter(X[:,0], X[:,1])
3. Проведем иерархическую кластеризацию выборки, используя разные способы вычисления расстояния между кластерами, и построим дендрограммы.
Используем расстояние ближайшего соседа:
mergings1 = linkage(X, method='single') fig, axes = plt.subplots(figsize=(30,15))
dn1=dendrogram(mergings1, leaf_font_size = 14)
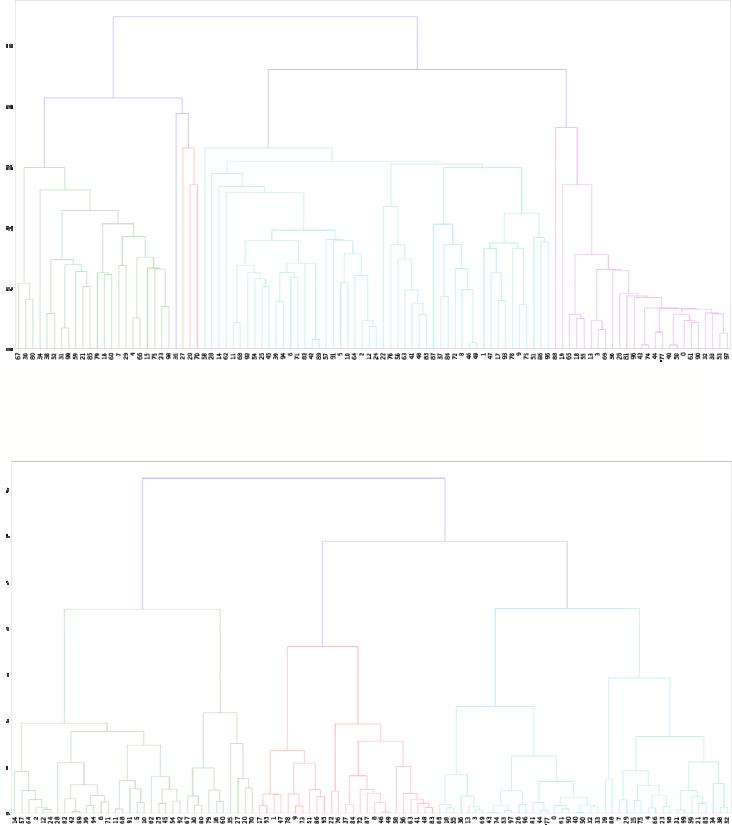
Используем расстояние дальнего соседа:
mergings2 = linkage(X, method='complete') fig, axes = plt.subplots(figsize=(30,15)) dn2=dendrogram(mergings2, leaf_font_size = 14)
2
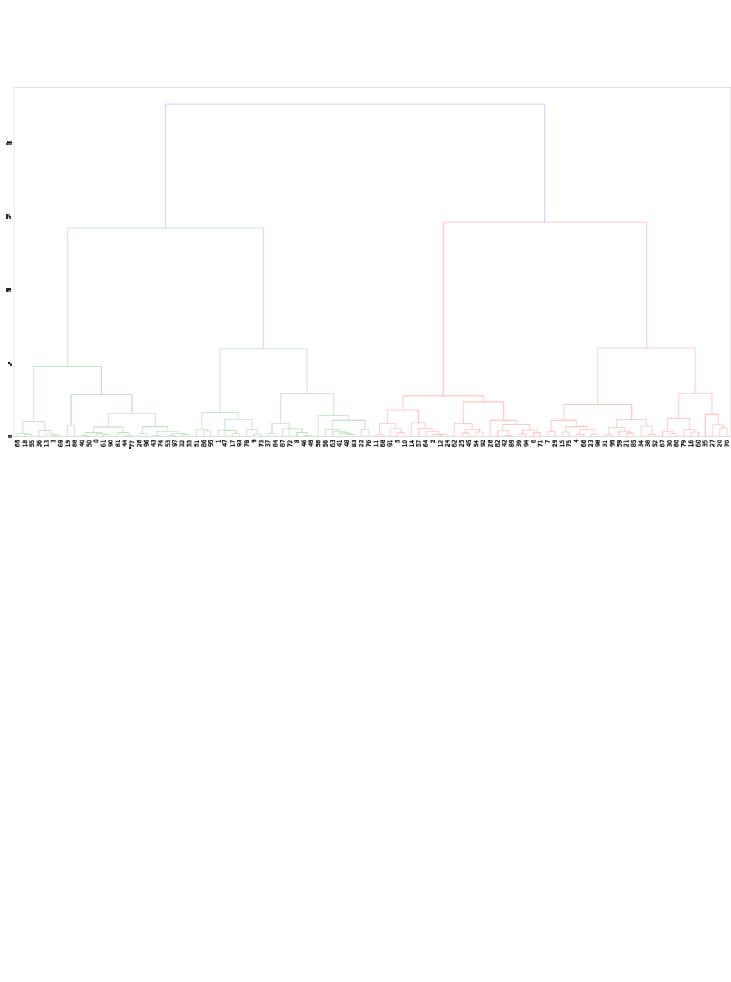
Используем расстояние Уорда:
mergings3 = linkage(X, method='ward') fig, axes = plt.subplots(figsize=(30,15))
dn3=dendrogram(mergings3, leaf_font_size = 14)
4. Выбор лучшего способа вычисления расстояния между кластерами.
Из дендрограмм видно, что провести горизонтальную прямую на наиболее высоком уровне позволяет дендрограмма с расстоянием Уорда.
5. Определение числа кластеров в имеющейся выборке для выбранного способа вычисления расстояния.
T = fcluster(mergings3, 10, 'distance') print(T)
[1 2 3 1 4 3 3 4 2 2 3 3 3 1 3 4 4 2 1 1 4 4 2 4 3 3 1 4 3 4 4 4 1 1 4 4 1 2 4 3 1 2 3 1 1 3 2 2 2 2 1 2 4 1 3 1 2 3 2 4 4 1 3 2 3 1 4 4 3 1 4 3 2 2 1 4 2 1 2 4 4 1 3 2 2 4 2 2 1 3 1 3 3 2 3 2 1 1 4 4]
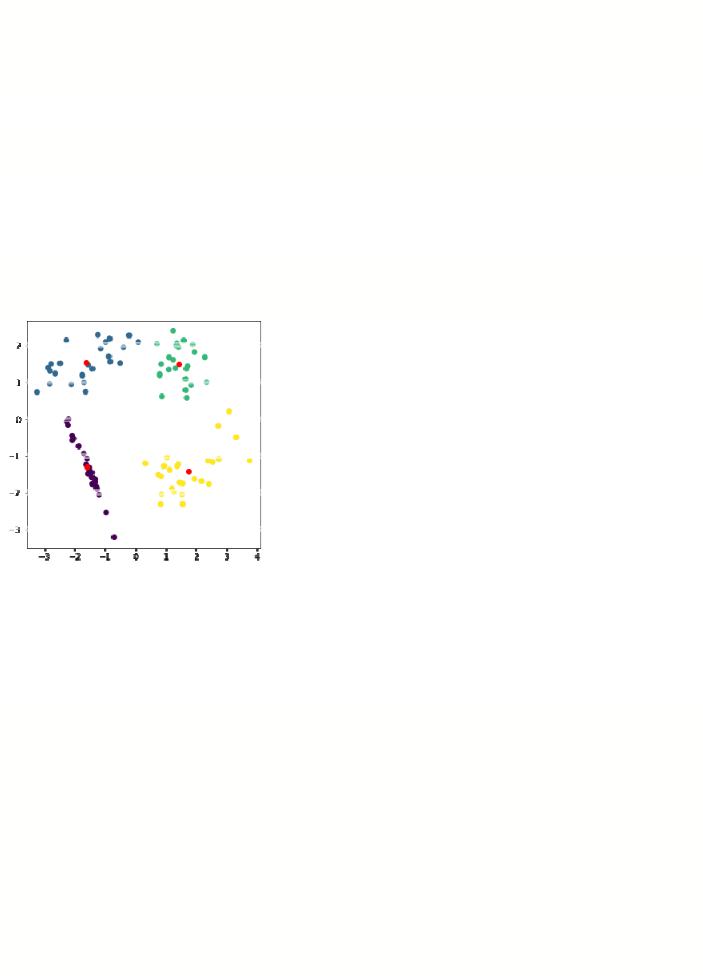
Видно, что получено 4 кластера, что совпадает с действительным числом кластеров в исходной выборке.
Функция расчета координат центроидов для 4 кластеров:
def update_cluster_centers(X, c): ix = np.where(c==1)
mu[0,:] = np.mean(X[ix,:], axis=1) ix = np.where(c==2)
mu[1,:] = np.mean(X[ix,:], axis=1)
3
ix = np.where(c==3)
mu[2,:] = np.mean(X[ix,:], axis=1) ix = np.where(c==4)
mu[3,:] = np.mean(X[ix,:], axis=1) return mu
mu = np.array([[0.0,0], [0,0], [0,0], [0,0]]) mu = update_cluster_centers(X,T)
print(mu)
[[-1.60522201 -1.30707562] [-1.64954738 1.52368342] [ 1.40862075 1.48625553] [ 1.71247983 -1.41618794]]
plt.scatter(X[:,0], X[:,1], c=T) plt.scatter(mu[:,0], mu[:,1], c="red")
6. Рассчитаем среднюю сумму квадратов расстояний до центроида, среднюю сумму средних внутрикластерных расстояний и среднюю сумму межкластерных расстояний для данного разбиения.
#Расчет средней суммы средних внутрикластерных расстояний def update_dist(X,T,mu):
dist = [0]*max(T)
for i in range(1,max(T)+1): ix = np.where(T==i)
X1 = X[ix,:]
for element in X1[0]:
dist[i-1] += euclidean_distances(element.reshape(1,-1), mu[i-1,:].reshape(1,-1))
dist[i-1] = dist[i-1] / len(X1[0])
S=0
for k in range(1,len(dist)+1): S += dist[k-1]
S = S / len(dist)
4

return S
S_vnytr = update_dist(X,T,mu)
print('Средняя сумма средних внутрикластерных расстояний:', str(S_vnytr). replace('[[', '').replace(']]', ''))
Средняя сумма средних внутрикластерных расстояний: 0.78598546
#Расчет средней суммы межкластерных расстояний def update_beetw(mu,T):
S = 0
for i in range(1,max(T)+1):
for j in range(1,max(T)+1): if i > j:
S += euclidean_distances(mu[i-1,:].reshape(1,-1), mu[j-1,:].reshape(1,-1))
S = S / max(T) return S
S_mez = update_beetw(mu,T)
print('Средняя сумма межкластерных расстояний:', str(S_mez).replace('[[', ''). replace(']]', ''))
Средняя сумма межкластерных расстояний: 5.17566459
#Расчет средней суммы квадратов расстояний до центра: def update_inertia(X,T,mu):
inert = [0]*max(T)
for i in range(1,max(T)+1): ix = np.where(T == i) X1 = X[ix,:]
for element in X1[0]:
inert[i-1] += math.pow(euclidean_distances(element.reshape(1,-1), mu[i-1,].reshape(1,-1)),2)
S=0
for k in range(1,len(inert)+1): S += inert[k-1]
S = S / len(inert) return S
S_cent = update_inertia(X,T,mu)
print('Средняя сумма квадратов расстояний до центра:',str(S_cent).replace('[[', '')
.replace(']]', ''))
Средняя сумма квадратов расстояний до центра: 20.94168509999429
5

Вывод: средняя сумма средних внутрикластерных расстояний достаточно мала, средняя сумма межкластерных расстояний не очень велика, средняя сумма квадратов расстояний до центра не очень велика. Так как оптимально было бы получить наименьшие значения средней суммы средних внутрикластерных расстояний и средней суммы квадратов расстояний до центра, а также наибольшее значение средней суммы межкластерных расстояний, можно сказать, что разбиение достаточно качественно.
7. Проведем кластеризацию выборки методом k-средних для k [1, 10] и построение графиков зависимости средней суммы квадратов расстояний до центроида, средней суммы средних внутрикластерных расстояний и средней суммы межкластерных расстояний от количества кластеров
k = 1 plot_inertia = [] plot_dist = [] plot_beetw = [] while k <= 10:
print('K =', k)
kmeans = KMeans(n_clusters = k) kmeans.fit(X)
all_predictions = kmeans.predict(X) print(all_predictions)
print('Средняя сумма квадратов расстояний до центра:', str(update_inertia(X, all_predictions + 1, kmeans.cluster_centers_)).replace('[[', '').replace(']]', ''))
plot_inertia.append(update_inertia(X, all_predictions + 1, kmeans.cluster_centers_))
print('Средняя сумма средних внутрикластерных расстояний:', str(update_dist(X, all_predictions + 1, kmeans.cluster_centers_)).replace('[[', '').replace(']]', ''))
plot_dist.append(update_dist(X, all_predictions + 1, kmeans.cluster_centers_)) print('Средняя сумма межкластерных расстояний:', str(update_beetw(kmeans.
cluster_centers_, all_predictions)).replace('[[', '').replace(']]', '')) plot_beetw.append(update_beetw(kmeans.cluster_centers_, all_predictions)) k += 1
print('------------------------------------------------------------------------
--------------------------') plt.clf()
plt.rcParams["figure.figsize"] = [5,5] plt.scatter(range(1,k), plot_inertia) plt.savefig('inertia.png')
plt.clf() plt.rcParams["figure.figsize"] = [5,5] plt.scatter(range(1,k), plot_dist) plt.savefig('dist.png')
plt.clf() plt.rcParams["figure.figsize"] = [5,5] plt.scatter(range(1,k), plot_beetw)
6

plt.savefig('beetw.png')
Результаты:
K = 1
[0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0]
Средняя сумма квадратов расстояний до центра: 545.7162442721158 Средняя сумма средних внутрикластерных расстояний: 2.28270153 Средняя сумма межкластерных расстояний: nan
---------------------------------------------------------------------------------------
-----------
K = 2
[0 0 1 0 1 1 1 1 0 0 1 1 1 0 1 1 1 0 0 0 1 1 0 1 1 1 0 1 1 1 1 1 0 0 1 1 0 0 1 1 0 0 1 0 0 1 0 0 0 0 0 0 1 0 1 0 0 1 0 1 1 0 1 0 1 0 1 1 1 0 1 1 0 0 0 1 0 0 0 1 1 0 1 0 0 1 0 0 0 1 0 1 1 0 1 1 0 0 1 1]
Средняя сумма квадратов расстояний до центра: 144.93385251944756 Средняя сумма средних внутрикластерных расстояний: 1.61859058 Средняя сумма межкластерных расстояний: 0.0
---------------------------------------------------------------------------------------
-----------
K = 3
[2 0 0 2 1 0 0 1 2 0 0 0 0 2 0 1 1 0 2 2 1 1 2 1 0 0 2 1 0 1 1 1 2 2 1 1 2 2 1 0 2 2 0 2 2 0 2 0 2 2 2 0 1 2 0 2 2 0 2 1 1 2 0 2 0 2 1 1 0 2 1 0 2 0 2 1 2 2 0 1 1 2 0 2 2 1 0 2 1 0 2 0 0 0 0 0 2 2 1 1]
Средняя сумма квадратов расстояний до центра: 54.509377955742046 Средняя сумма средних внутрикластерных расстояний: 1.11491708 Средняя сумма межкластерных расстояний: 1.60863459
---------------------------------------------------------------------------------------
-----------
K = 4
[0 3 1 0 2 1 1 2 3 3 1 1 1 0 1 2 2 3 0 0 2 2 3 2 1 1 0 2 1 2 2 2 0 0 2 2 0 3 2 1 0 3 1 0 0 1 3 3 3 3 0 3 2 0 1 0 3 1 3 2 2 0 1 3 1 0 2 2 1 0 1 1 3 3 0 2 3 0 3 2 2 0 1 3 3 2 3 3 0 1 0 1 1 3 1 1 0 0 2 2]
Средняя сумма квадратов расстояний до центра: 20.565167796129085 Средняя сумма средних внутрикластерных расстояний: 0.78331925 Средняя сумма межкластерных расстояний: 3.4397037
---------------------------------------------------------------------------------------
-----------
K = 5
[2 1 3 2 0 3 3 0 4 1 3 3 3 2 3 0 0 1 4 2 0 0 4 0 3 3 2 0 3 0 0 0 2 2 0 0 2 1 0 3 2 4 3 2 2 3 4 1 4 4 2 1 0 2 3 4 4 3 4 0 0 2 3 4 3 4 0 0 3 2 3 3 4 1 2 0 4 2 1 0 0 2 3 4 1 0 1 4 2 3 2 3 3 1 3 1 2 2 0 0]
Средняя сумма квадратов расстояний до центра: 12.702615089960592 Средняя сумма средних внутрикластерных расстояний: 0.66300224 Средняя сумма межкластерных расстояний: 5.05235661
---------------------------------------------------------------------------------------
-----------
K = 6
[4 2 0 4 1 0 0 1 5 2 0 0 0 4 0 1 3 2 5 4 3 1 5 1 0 0 4 3 0 1 3 1 4 4 1 3 4 2 1 0 4 5 0 4 4 0 5 2 5 5 4 2 1 4 0 5 5 0 5 1 1 4 0 5 0 5 1 3 0 4 3 0 5 2 4 1 5 4 2 3 3 4 0 5 2 1 2 5 4 0 4 0 0 2 0 2 4 4 1 1]
Средняя сумма квадратов расстояний до центра: 7.594267597242438 Средняя сумма средних внутрикластерных расстояний: 0.60069013 Средняя сумма межкластерных расстояний: 6.63818446
---------------------------------------------------------------------------------------
-----------
K = 7
[3 6 2 0 1 2 2 1 4 6 2 2 2 0 2 1 5 6 0 3 5 1 4 1 2 2 0 5 2 1 5 1 3 3 1 5 0 4 1 2 3 4 2 3 3 2 4 6 4 4 3 6 1 3 2 0 4 2 4 1 1 3 2 4 2 0 1 5 2 0 5 2 4 6 3 1 4 3 6 5 5 3 2 4 4 1 6 4 3 2 3 2 2 6 2 6 3 3 1 1]
Средняя сумма квадратов расстояний до центра: 5.196814510384003
7
Средняя сумма средних внутрикластерных расстояний: 0.51848191 Средняя сумма межкластерных расстояний: 8.48663484
---------------------------------------------------------------------------------------
-----------
K = 8
[4 0 3 2 1 3 7 1 6 0 3 7 3 2 3 1 1 0 2 4 5 1 6 1 3 7 2 5 7 1 5 1 4 4 1 5 2 6 1 3 4 6 7 4 4 7 6 0 6 6 4 0 1 4 7 2 6 3 6 1 1 4 7 6 3 2 1 5 7 2 5 7 6 0 4 1 6 4 0 1 5 4 7 6 6 1 0 6 4 7 4 3 7 0 3 0 4 4 1 1]
Средняя сумма квадратов расстояний до центра: 4.024311349980351 Средняя сумма средних внутрикластерных расстояний: 0.49161199 Средняя сумма межкластерных расстояний: 10.30560893
---------------------------------------------------------------------------------------
-----------
K = 9
[6 3 2 1 0 2 2 0 5 3 2 8 2 1 2 0 7 3 1 6 4 0 5 0 2 8 1 4 8 0 7 0 6 6 0 4 1 3 0 2 6 5 2 6 6 8 5 3 5 5 6 3 0 6 8 1 5 2 5 0 7 6 8 5 2 1 0 7 8 1 4 2 5 3 6 0 5 6 3 7 7 6 2 5 3 0 3 5 6 2 6 8 8 3 2 3 6 6 0 0]
Средняя сумма квадратов расстояний до центра: 3.1738672965732153 Средняя сумма средних внутрикластерных расстояний: 0.46099418 Средняя сумма межкластерных расстояний: 12.00712868
---------------------------------------------------------------------------------------
-----------
K = 10
[4 3 7 1 2 7 0 2 8 3 7 0 7 1 7 2 2 3 1 9 6 2 5 2 7 0 1 6 0 2 6 2 4 4 2 6 1 8 2 7 4 5 0 4 4 0 8 3 5 8 4 3 2 4 0 1 5 7 5 2 2 4 0 5 7 1 2 6 0 1 6 0 8 3 4 2 5 4 3 2 6 4 7 5 8 2 3 8 9 0 4 0 0 3 7 3 4 4 2 2]
Средняя сумма квадратов расстояний до центра: 2.441688888684171 Средняя сумма средних внутрикластерных расстояний: 0.41439014 Средняя сумма межкластерных расстояний: 12.89424639
---------------------------------------------------------------------------------------
-----------
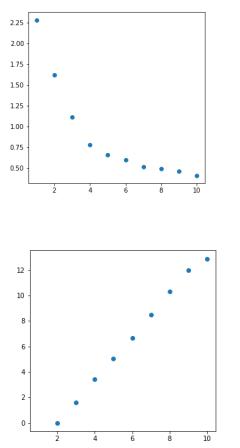
dist.png (средние суммы средних внутрикластерных расстояний):
beetw.png (средние суммы межкластерных расстояний):
inertia.png (средние суммы квадратов расстояний до центроида):
8
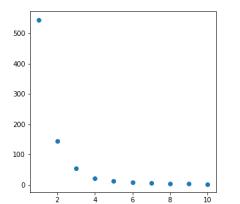
Из полученных графиков видно, что с увеличением числа кластеров значения средней суммы средних внутрикластерных расстояний и средней суммы квадратов расстояний до центра убывают, а значение средней суммы межкластерных расстояний возрастает.
Так как оптимально было бы получить наименьшие значения средней суммы средних внутрикластерных расстояний и средней суммы квадратов расстояний до центра, а также наибольшее значение средней суммы межкластерных расстояний, при этом число кластеров не должно быть слишком велико, выберем оптимальное число кластеров 4 (на сгибе рисунков dist.png и inertia.png). Выбранное количество кластеров совпадает с числом кластеров исходной выборки.
8. Составим сравнительную таблицу результатов разбиения иерархическим методом и методом k-средних.
|
|
Средняя |
Средняя |
Средняя |
|
|
Число |
сумма средних |
сумма квадратов |
||
Метод |
сумма межкластерных |
||||
кластеров |
внутрикластерных |
расстояний |
|||
|
|
расстояний |
расстояний |
до центра |
|
|
|
|
|||
Иерархический |
|
0,79 |
5,18 |
20,94 |
|
(с расстоянием |
4 |
||||
Уорда) |
|
|
|
|
|
|
1 |
2,28 |
- |
545,72 |
|
|
2 |
1,62 |
0 |
144,93 |
|
|
3 |
1,11 |
1,61 |
54,51 |
|
|
4 |
0,78 |
3,44 |
20,57 |
|
k-средних |
5 |
0,66 |
5,05 |
12,70 |
|
6 |
0,60 |
6,64 |
7,59 |
||
|
|||||
|
7 |
0,52 |
8,47 |
5,20 |
|
|
8 |
0,49 |
10,31 |
4,02 |
|
|
9 |
0,46 |
12,01 |
3,17 |
|
|
10 |
0,41 |
12,89 |
2,44 |
Вывод: из таблицы видно, что и метод иерархической кластеризации (при расчете расстояния Уорда), и метод k-средних при числе кластеров 4 позволяют получить достаточно близкие значения характеристик качества. Кластеризацию, проведенную обоими методами с указанными параметрами, можно считать успешной.
9
