
bileti_linal задачи
.docxВариант 1.
В вариантах различаются 2 и 3 номера.
вариантах различаются 2 и 3 номера.

Задача 1. Ядро и образ линейного оператора. Теорема о размерности ядра и образа линейного оператора (с док-вом).

Задача
2. Найти базис ортогонального дополнения
L
подпространства L,
построенного на векторах а1, а2, а3.


Задача 3. Найти область значений и ядро линейного оператора f: X -> X, заданного в некотором базисе e1, e2, e3 матрицей:

Задача 4.
Вариант 2
Различается 3 номер.


Задача 1. Разложение евклидова пространства L в прямую сумму любого его подпространства L1 L и ортогонального дополнения к L1 (с док-вом).

Задача 2. Найти ортогональную проекцию вектора x на линейную оболочку L(a1, a2), где a1 и a2:

Задача 3. Найти собственные значения и собственные векторы оператора. Приводится ли оператор к диагональному виду? Если да, то привести в диагональный вид.


Вариант 3
2 и 3 номера различаются.


Задача 1. Правило Крамера решения системы линейных алгебраических уравнений (с док-вом).


Задача 2. Найти какой-нибудь базис и определить размерность пространства решений системы:

Задача 3. Найти матрицу в базисе (i, j, k) оператора симметрии относительно плоскости x+2y+z=0:

Вариант №4


Задача 1. Пересечение и сумма подпространств. Теорема о размерности суммы и пересечения двух подпространств (с док-вом).

Задача 2. Найти размерность суммы и пересечения линейных подпространств, построенных на системах векторов a1, a2, a3 и b1, b2, b3:

Задача 3. Найти собственные значения и собственные векторы оператора, заданного матрицей:
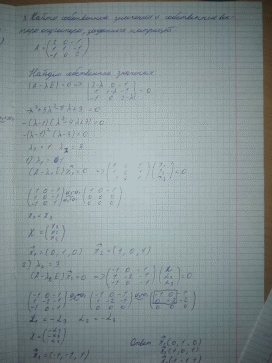
Вариант №5


Задача 1. Евклидовы пространства. Определение и примеры. Норма элемента. Неравенство Коши-Буняковского и неравенство треугольника (с док-вами). Угол между элементами.


Задача 2. Найти площадь треугольника, вершины которого заданы своими координатами A, B, C:

Задача 3. Найти собственные значения и собственные векторы оператора. Приводится ли оператор к диагональному виду? Если да, то привести в диагональный вид.

Вариант №6
2 номер различается.


Задача 1. Обратная матрица. Теорема об обратной матрице (с док-вом).

Задача 2. Дана матрица Ае оператора А в базисе e1, e2, дана матрица Bf оператора B в базисе f1 = e1+e2, f2 = e1-e2. Найдите матрицу оператора (AB)^2 в базисе f1, f2:

Задача 3. Найти ортогональное преобразование, приводящую квадратную форму к каноническому виду, и написать этот канонический вид (x1)^2+(x2)^2-6x1x2

Билет №7



Задача 1. Координаты вектора в данном базисе. Действия с координатами. Преобразование координат при переходе к новому базису (с док-вом).

Задача 2. Найти координаты вектора x=e1+2e2+3e3 в базисе f1=e1+e2+e3, f2=e1+e2, f3=e3

Задача 3. Привести квадратную форму к нормальному виду методом Лагранжа:

Вариант №8
2 номер различается.


Задача 1. Диагональный вид матрица линейного оператора. Достаточное условие приводимости матрицы оператора к диагональному виду (с док-вом).

Задача 2. Найти диагональный вид матрицы оператора и соответствующий базис из собственных векторов:
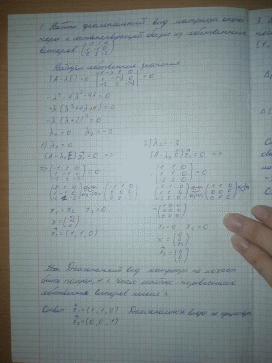
Задача 3. Найти объем параллелепипеда, построенного на векторах. Найти высоту.

Вариант №9



Задача 1. Теорема Кронекера-Капелли (с док-вом).

Задача 2. Привести форму к каноническому виду с помощью метода Лагранжа:
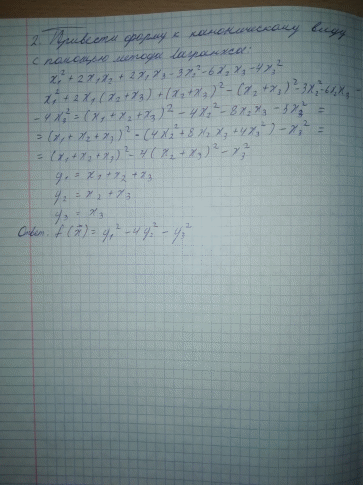
Задача 3. Найти ядро и образ оператора с матрицей:

Билет №10
2 и 3 номера различаются.
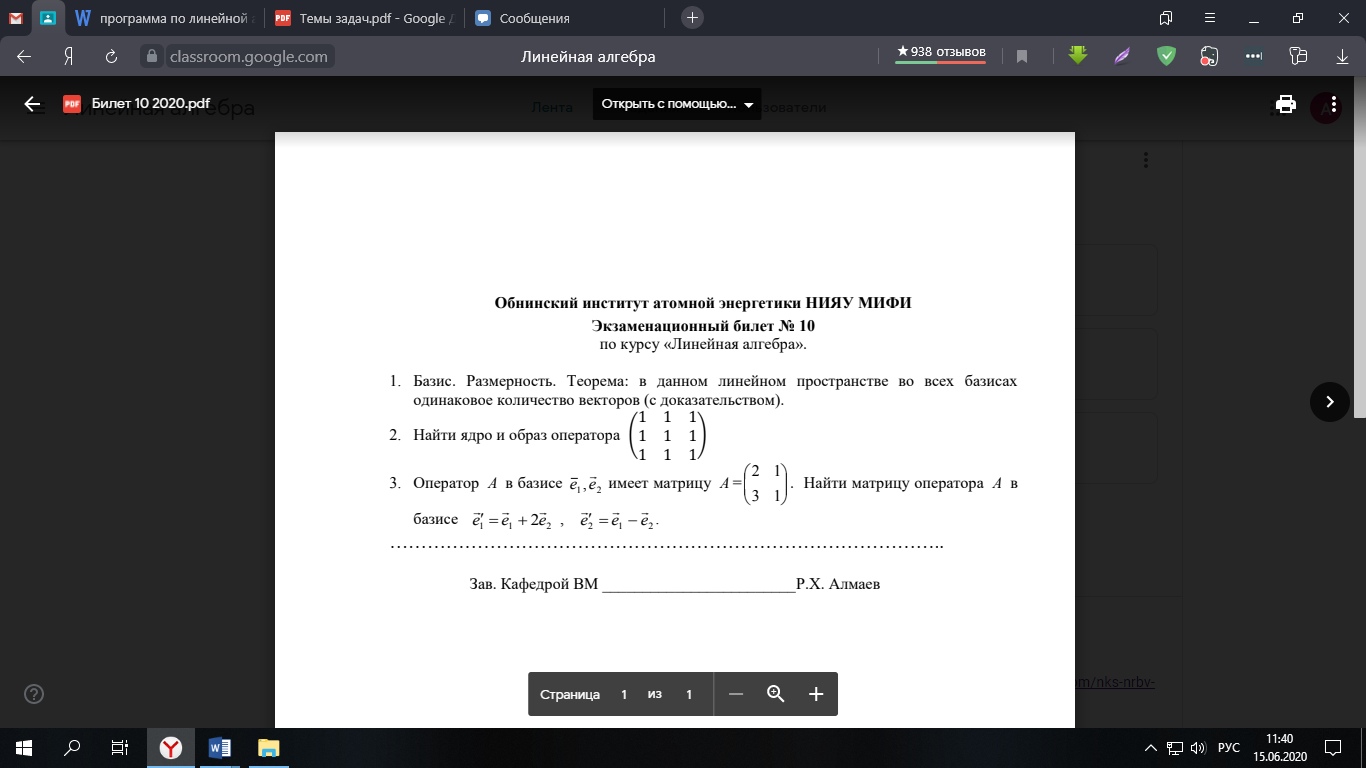

Задача 1. Базис. Размерность. Теорема: в данном линейном пространстве во всех базисах одинаковое количество векторов (с док-вом).

Задача 2. Найти ядро и образ оператора:

Задача 3. Оператор А в базисе e1, e2 имеет матрицу А. Найти матрицу оператора А в базисе e1 = e1+2e2, e2 = e1-e2:

Билет №11
2 и 3 номера различаются.
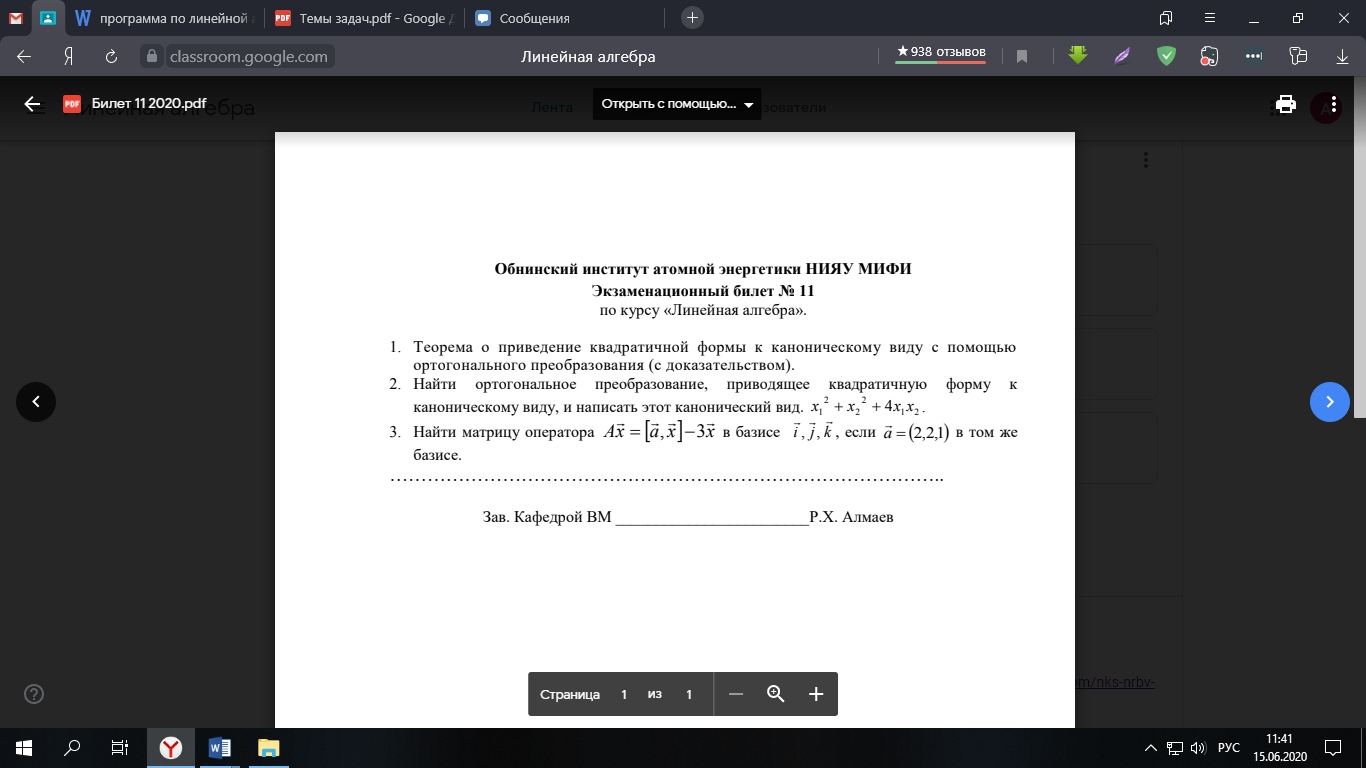

Задача 1. Теорема о приведение квадратичной формы к каноническому виду с помощью ортогонального преобразования (с док-вом).

Задача 2. Найти ортогональное преобразование, приводящее квадратичную форму к каноническому виду, и написать этот канонический вид:

Задача 3. Найти матрицу оператора Ax-3x в базисе i,j,k, если а в том же базисе:

Билет №12
2 и 3 номера различаются.
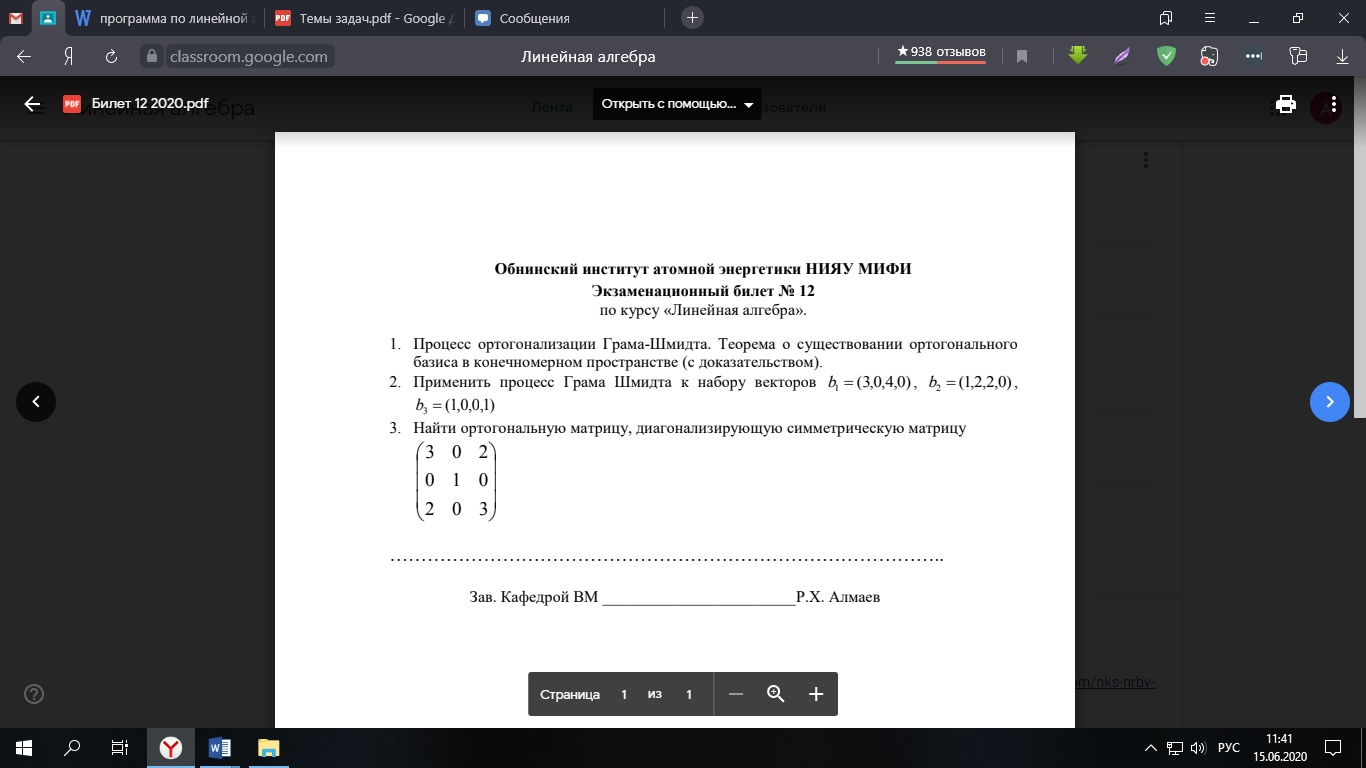


Задача 1. Процесс ортогонализации Грама-Шмидта. Теорема о существовании ортогонального базиса в конечномерном пространстве (с док-вом).

Задача 2. Применить процесс Грамма Шмидта к набору векторов:

Задача 3. Найти ортогональную матрицу, диагонализирующую симметрическую матрицу:

Билет №13
2 и 3 номера различаются.
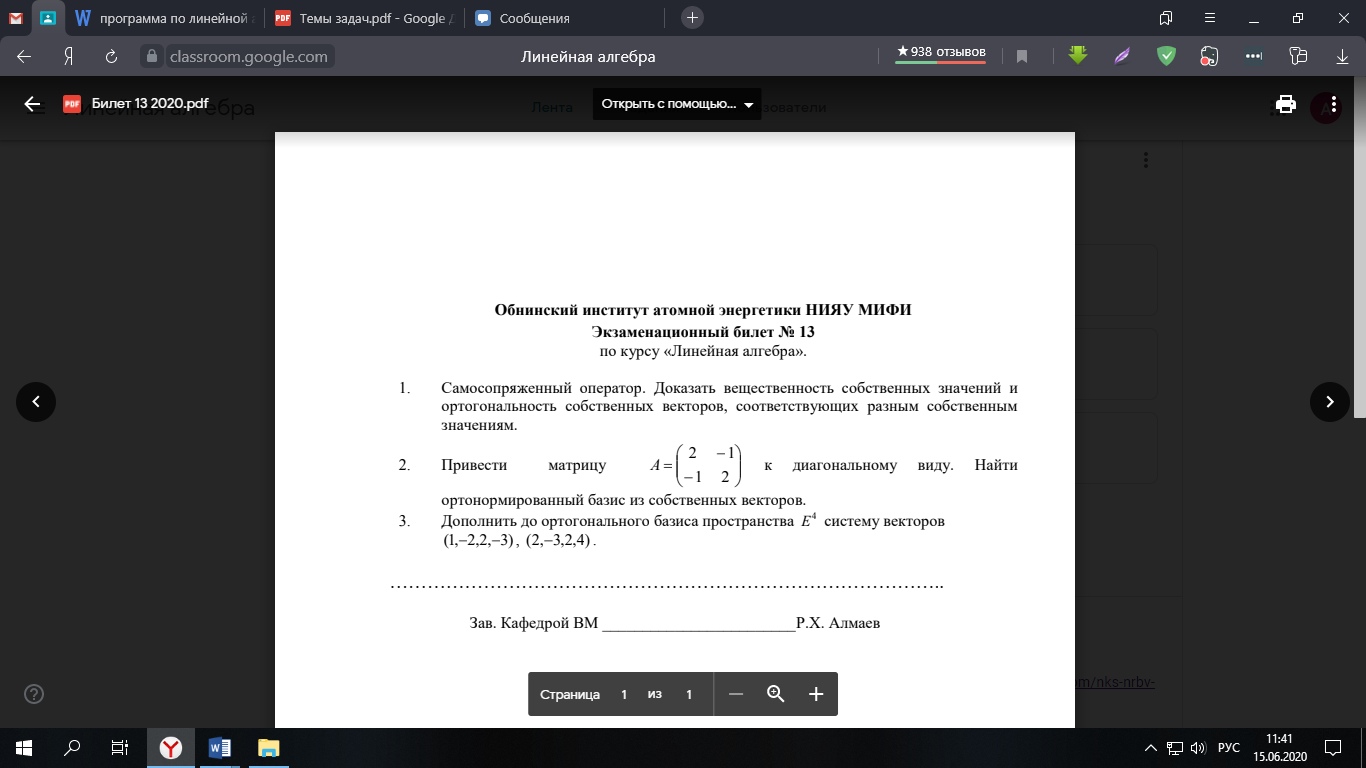

Задача 1. Самосопряженный оператор. Доказать вещественность собственных значений и ортогональность собственных векторов, соответствующих разным, собственным значениям.

Задача 2. Привести матрицу к диагональному виду. Найти ортонормированный базис из собственных векторов.

Задача 3. Дополнить до ортогонального базиса пространства Е^4 систему векторов.
Билет №14


Задача 1. Характеристический многочлен оператора, его инвариантность (с док-вом).

Задача 2. Оператор А в базисе е1, е2 имеет матрицу. Найти матрицу А^2 в базисе е1 = е1+е2, е2 = е1-2е2

Задача 3. Найти собственные векторы и собственные значения оператора, заданного матрицей. Приводится ли оператор к диагональному виду? Если да, то найти диагональный вид и диагонализирующую матрицу.


Билет №15
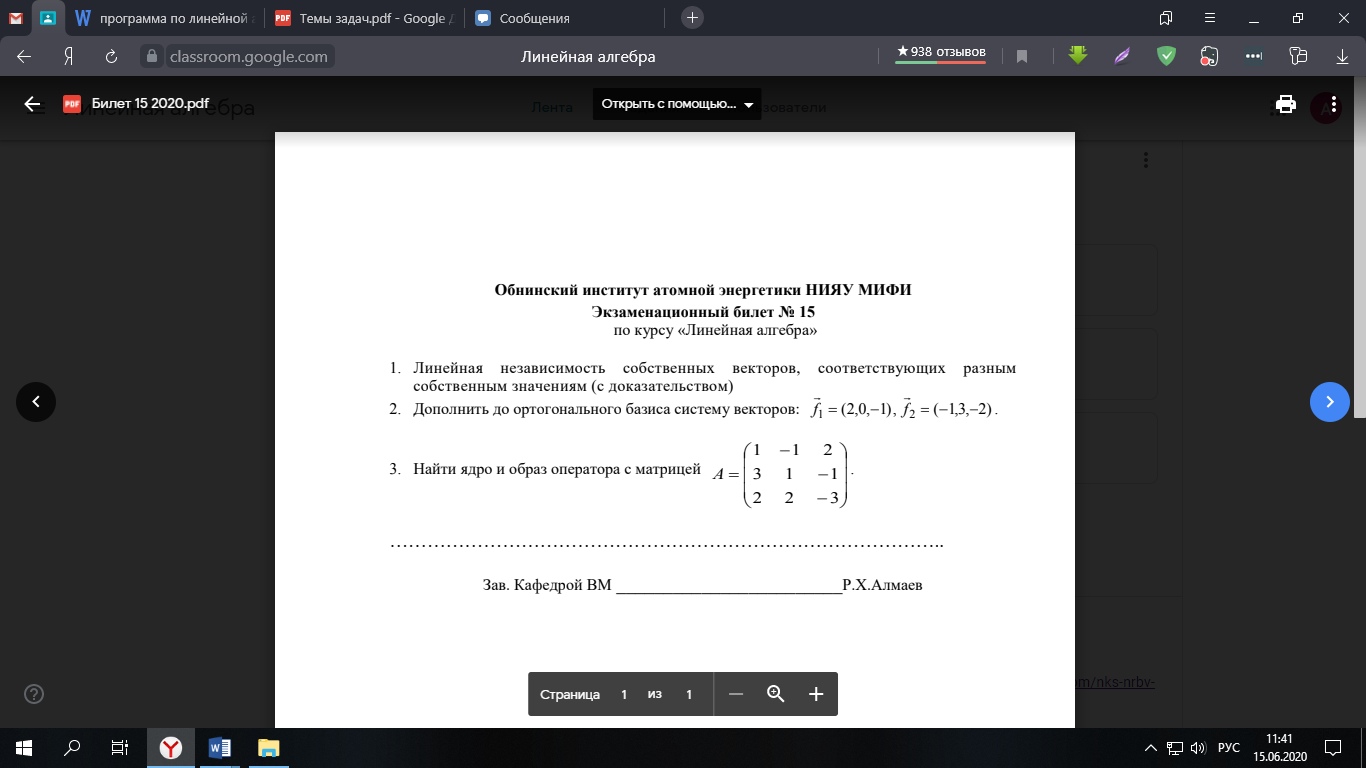


Задача 1. Линейная независимость собственных векторов, соответствующих разным собственным значениям (с док-вом).

Задача 2. Дополнить до ортогонального базиса систему векторов f1 и f2

Задача 3. Найти ядро и образ оператора с матрицей.

Билет №16
3 номер различается.
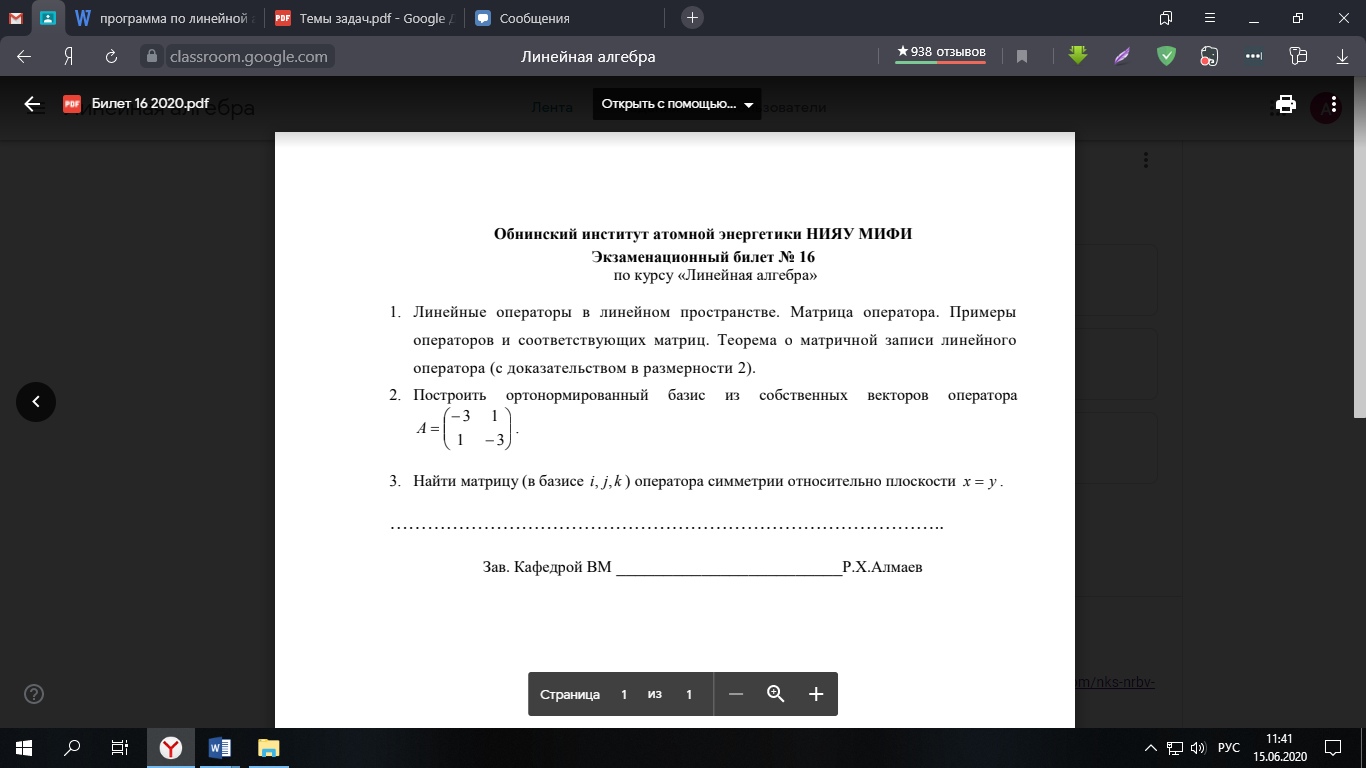

Задача 1. Линейные операторы в линейном пространстве. Матрица оператора. Примеры операторов и соответствующих матриц. Теорема о матричной записи линейного оператора (с док-вом).





Задача 2. Построить ортонормированный базис из собственных векторов оператора.

Задача 3. Найти матрицу (в базисе i,j,k) оператора симметрии относительно плоскости x = y

Билет №17
3 номер различается.

Задача 1. Подпространства линейного пространства. Линейная оболочка векторов. Размерность подпространства. Теорема о размерности линейной оболочки (с док-вом).




Задача 2. Проверить, что векторы ортогональны, и дополнить их до ортогонального базиса.


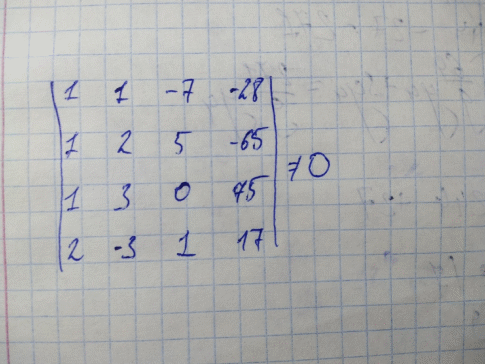
Задача 3. Найти собственные значения и собственные векторы оператора, заданного матрицей.

Билет №18

Задача 1. Пересечение и сумма подпространств. Теорема о размерности суммы и пересечения двух подпространств (с док-вом).
Задача 2. Найти базис ортогонального дополнения L подпространства L, построенного на векторах а1, а2, а3.
Задача 3. Найти область значений и ядро линейного оператора f: X -> X, заданного в некотором базисе e1, e2, e3 матрицей:
Билет №19

Задача 1. Евклидовы пространства. Определение. Примеры. Неравенство Коши-Буняковского. Норма элемента. Неравенство треугольника.
Задача 2. Найти объем параллелепипеда, построенного на векторах.

Задача 3. Найти собственные значения и собственные векторы оператора, заданного матрицей. Найти диагональный вид, если он существует.


Билет №20


Задача 1.
Задача 2.
Задача 3. Найти матрицу в базисе I j k оператора относительно плоскости x+2y+z=0




Билет №21

Задача 1.
Задача 2.

Задача 3.

