Равновесие системы сходящихся сил

Система сходящихся сил – это силы, сходящиеся в одной точке (рис. 2.6).

Геометрическое условие равновесия. Для равновесия системы сходящихся сил необходимо и достаточно, чтобы силовой многоугольник, построенный на этих силах, был замкнут.

А

Рис. 2.6

налитические условия равновесия. Для равновесия пространственной системы сходящихся сил необходимо и достаточно, чтобы суммы проекций этих сил на каждую из трех координатных осей были равны нулю.

F_kx = 0; F_ky = 0; F_kz = 0.

Теорема о трех силах. Если свободное твердое тело находится в состоянии равновесия под действием трех непараллельных сил, лежащих в одной плоскости, то линии действия этих сил пересекаются в одной точке.

F ₁ + F₂ + F₃ = 0

Системы статически определимые и статически неопределимые

Задача статики может быть решена лишь в том случае, когда для нее число неизвестных реакций связей не превышает число уравнений равновесия, содержащих эти реакции. Такие задачи называют статически определенные, а система тел, для которых это имеет место – статически определимыми системами.

Задачи, в которых число неизвестных реакций связей больше числа уравнений равновесия, содержащих эти реакции, называются статически неопределенные, а система тел для которых это имеет место – статически неопределимыми системами.

П

Рис. 2.7

римером для статически неопределенной системы может служить груз, подвешенный на трех нитях, лежащих в одной плоскости (рис. 2.7). В этой задаче три неизвестные силы натяжения нити T₁, T₂, T₃, а уравнений равновесия в случае плоской системы сходящихся сил можно составить только два.

Решение задач статики

Для решения задач статики необходимо:

1. Выбрать тело, равновесие которого должно быть рассмотрено.

2. Освобождение тела от связей и изображение действующих на него заданных сил и реакций отброшенных связей.

3. Составление уравнений равновесия.

4. Определение искомых величин, проверка правильности решения и исследование полученных результатов.

Для решения задач на равновесие тела под действием сходящихся сил можно использовать следующие способы:

а ) Геометрический способ. Применяется если число сил, действующих на тело равно трем. При равновесии треугольник, построенный на этих силах, должен быть замкнутым.

б) Аналитический способ. Применяется при любом количестве сил, действующих на тело. В случае плоской системы сходящихся сил составляется два уравнения равновесия, а в случае пространственной системы сил – три.

Рис. 2.8а

П ример №3. К вертикальной гладкой стене АВ подвешен на тросе АС однородный шар. Трос составляет со стеной угол , сила тяжести шара Р. Определить силу натяжения троса Т и давление шара на стену Q. Шар находится в равновесии под действием этих трех сил (рис. 2.8а).

Решение.

Р ассмотрим решение задачи геометрическим (графическим) способом. Так как шар находится в равновесии под действием трех сил, то эти силы сходящиеся. Точка, в которой сходятся эти силы, является геометрическим центром шара (точка О). Построим силовой треугольник (рис. 2.8б). Построение начинают с известной силы Р.

Силовой треугольник должен быть замкнут. В данном случае это прямоугольный треугольник. Тогда: ;

О

Рис. 2.8б

твет: ; .

П

А

а)

б)

в)

Рис. 2.9

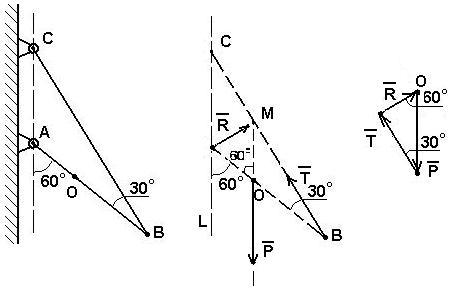
ример №4. Однородный стержень АВ прикреплен к стенке посредством шарнира А и удерживается под углом 60⁰ к вертикали при помощи троса ВС, образующего с ним угол 30⁰ (рис. 2.9а). Определить величину и направление реакции R шарнира, если известно, что вес стержня равен 20Н.

Решение:

Определим силы, действующие на данную конструкцию:

Р – сила тяжести стержня АВ, так как стержень однородный, то сила приложена к его геометрическому центру (точка О).

Т – натяжение троса СВ, направлено вдоль СВ.

R – реакция в шарнире А (направление неизвестно) (рис. 2.9б).

Согласно принципу освобождаемости от связей, заменим связи соответствующими реакциями.

Так как система находится в равновесии под действием трех сил, то эти силы должны сходиться, а поэтому сила реакции R направлена от А к М (точка пересечения сил Р и Т).

Построим силовой треугольник. Для этого выберем произвольную точку О и отложим от нее известную силу Р, сохраняя ее направление. Из конца вектора Р под углом 30⁰ проведем луч, который соответствует направлению силы Т (рис. 2.9в).

Так как <LAO = <AOM (как накрест лежащие углы), то угол <MOB = 180⁰ - 60⁰ = 120⁰, тогда <OMB = 180⁰ – (120⁰ + 30⁰) = 30⁰, т.е. треугольник ОМВ равнобедренный: сторона ОМ = ОВ. Поэтому ОМ = ОВ = ОА, так как О является серединой АВ, а угол <АOM = 60⁰, то треугольник АОМ является равносторонним. Поэтому <OАM = 60⁰ = <AMO. Из точки О проводим луч под углом 60⁰ к направлению силы Р до пересечения с направлением силы Т. Полученный треугольник прямоугольный, поэтому R = Psin30⁰ = 20/2 = 10H.

Ответ: R = 10H.

Пример №5. Три груза А, В и С массой 10, 20, и 60 кг соответственно лежат на плоскости, наклоненной под углом  к горизонту (рис. 2.10). Грузы соединены тросами, как показано на рисунке. Коэффициенты трения между грузами и плоскостью равны _А = 0,1, _В = 0,25, _С = 0,5 соответственно.

Определить угол , при котором тела равномерно движутся вниз по плоскости. Найти также натяжение тросов Т_АВ и Т_ВС.

Р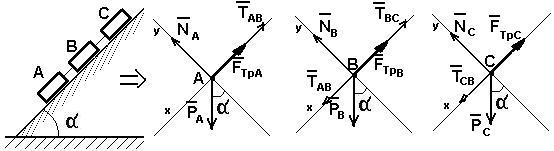 ешение:

Р

а)

б)

в)

г)

Рис. 2.10

ассмотрим, какие силы действуют на каждое тело и запишем условие равновесия, так как тела движутся равномерно, то

с умма всех сил, действующих на тело равна нулю. На тело А действует сила тяжести Р_А, сила реакции опоры N_А, сила трения F_трА и сила натяжения троса Т_АВ (рис. 2.10б). Условие равновесия: Р_А + N_А + F_трА + Т_АВ = 0.

Выберем систему координат и спроектируем силы на оси:

Ось ОХ Р_Аsin - Р_Аcos - Т_АВ = 0.

Подставляя численные значения получим: 10sin - cos - Т_АВ = 0.

Р ассмотрим, какие силы действуют на тело В: Р_В - сила тяжести, F_трВ - сила трения, Т_ВА- сила натяжения троса со стороны груза А, Т_ВС - сила натяжения троса со стороны груза С, N_В - сила реакции опоры (рис. 2.10в). Тогда условие равновесия будет: Р_В + N_В + F_трВ + Т_ВА + Т_ВС = 0.

Проектируя это уравнение на ось ОХ, получим:

Р_Вsin - F_трВ + Т_ВА - Т_ВС = 0; учитывая, что Т_ВА = Т_АВ:

Р_Вsin - Р_Вcos*_В + Т_ВА - Т_ВС = 0;

30sin - 30cos*0.25 + Т_ВА - Т_ВС = 0;

Н а тело С действуют следующие силы: Р_С - сила тяжести, F_трС - сила трения, Т_СВ- сила натяжения троса со стороны груза В, N_С - сила реакции опоры (рис. 2.10г). Тогда условие равновесия при проектировании на ось ОХ будет:

Р_Сsin - Р_Сcos*_С – Т_СВ = 0; так как Т_ВС = Т_СВ,

60sin - 60*0,5cos – Т_ВС = 0.

Получим систему из трех уравнений с тремя неизвестными:

Так как неизвестные силы перпендикулярны оси y, то на эту ось силы не проектируем.

1 0sin - cos - Т_АВ = 0 (1);

30sin - 7,5cos + Т_ВА - Т_ВС = 0 (2);

60sin - 30cos – Т_ВС = 0 (3).

Отсюда: Т_АВ = 10sin - cos; Т_ВС = 60sin - 30cos.

Подставляя выражения Т_АВ и Т_ВС в уравнение (2), получим:

100sin = 38.5cos; tg = 0.385;  = arctg0.385;  = 21⁰.

Из уравнения (1) получим: Т_АВ = 10sin21⁰ - cos21⁰ = 10*0,358 – 0,93 = 2,67Н.

Т_АВ = 2,67Н.

Подставляя численные данные в уравнение (3), получим:

Т_ВС = 60sin21⁰ - 30cos21⁰ = 60*0,358 – 30*0,93 = 6,42Н;

Т_ВС = 6,42Н.

Ответ:  = 21⁰; Т_АВ = 2,67Н; Т_ВС = 6,42Н.