теормех / ОТВЕТЫ ТЕОРМЕХ

Рассмотренные ниже примеры дают результаты, которыми можно непосредственно пользоваться при решении задач.

у1, z1). Выберем оси координат так, чтобы ось Oz была направлена вертикально вверх (рис.4).

71

Рис.4

Тогда Рx=0, Рy=0, Pz= -Р. Подставляя эти значения и учитывая переменную интегрирования z:

Если точка M0 выше М1, то , где h-величина вертикального перемещения точки;

Если же точка M0 ниже точки M1 то .

Окончательно получаем: .

Следовательно, работа силы тяжести равна взятому со знаком плюс или минус произведению модуля силы на вертикальное перемещение точки ее приложения. Работа положительна, если начальная точка выше конечной, и отрицательна, если начальная точка ниже конечной. Из полученного результата следует, что работа силы тяжести не зависит от вида той траектории, по которой перемещается точка ее приложения.

Силы, обладающие таким свойством, называются потенциальными.

2) Работа силы упругости. Рассмотрим груз М, лежащий на горизонтальной плоскости и прикрепленный к свободному концу некоторой пружины (рис.5,а). Отметим на плоскости точкой О положение, занимаемое концом пружины, когда она не напряжена ( - длина ненапряженной пружины), и примем эту точку за начало координат. Если теперь оттянуть груз от равновесного положения О, удлинив пружину до величины l, то на груз будет действовать сила упругости пружины F, направленная к точке О.

Рис.5

72

По закону Гука величина этой силы пропорциональна удлинению

равным силе, которую надо приложить к пружине, чтобы растянуть ее на 1 см.

Найдем работу, совершаемую силой упругости при перемещении груза из положения в положение Так как в данном случае Fx=-F=-cx, Fy=Fz=0, то получим:

т.е. работа силы упругости равна половине произведения коэффи-

циента жесткости на разность квадратов начального и конечного удлинений (или сжатий) пружины.

Работа будет положительной, когда , т. е. когда конец пружины перемещается к равновесному положению, и отрицательной, когда , т.е. конец пружины удаляется от равновесия положения. Можно доказать, что формула остается справедливой и в случае, когда перемещение точки М не является прямолинейным.

Таким образом, оказывается, что работа силы F зависит только от значений и и не зависит от вида траектории точки М. Следовательно, сила упругости также является потенциальной.

73

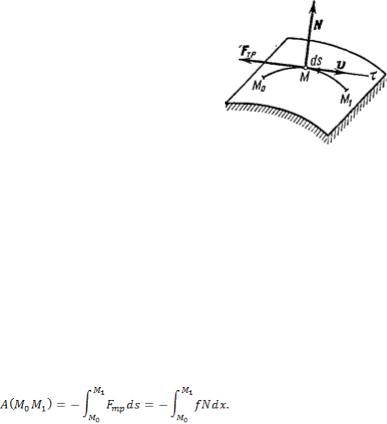
Рис.6

3) Работа силы трения. Рассмотрим точку, движущуюся по какой-нибудь шероховатой поверхности (рис.6) или кривой. Действующая на точку сила трения равна по модулю fN, где f - коэффициент трения, а -нормальная реакция поверхности. Направлена сила трения противоположно перемещению точки. Следовательно, Fтр=-fN и по формуле

Если величина силы трения постоянна, то , где s-длина дуги кривой М0М1 по которой перемещается точка.

Таким образом, работа силы трения при скольжении всегда отрицательна. Величина этой работы зависит от длины дуги М0М1 . Следовательно, сила трения является силой непотенциальной.

4) Работа силы, приложенной к телу, вращающемуся вокруг

неподвижной оси.

В этом случае (рис.7) точка приложения силы 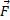движется по окружности радиуса r. Элементарная работа, по (1), , где .

74

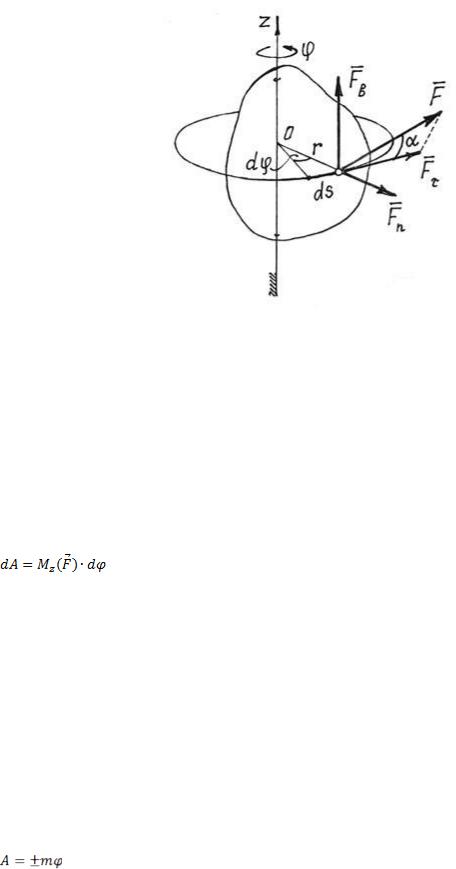
Рис.7

Поэтому .

Но .

Это нетрудно установить, разложив силу на три составляющие (рис. 7). (Моменты сил и равны нулю). Значит,

(2)

В частности, если момент силы относительно оси , работа силы при повороте тела на угол равна

. (3)

Знак работы определяется знаками момента силы и угла поворота. Если они одинаковы, работа положительная.

Из формулы (3) следует и правило определения работы пары сил. Если пара с моментом m расположена в плоскости перпендикулярной оси вращения тела, то ее работа при повороте тела на угол

Если же пара сил действует в плоскости не перпендикулярной оси вращения, то ее надо заменить двумя парами. Одну расположить в плоскости перпендикулярной оси, другую – в плоскости параллельной оси. Моменты их определяются разложением вектора момента по соответствующим

75

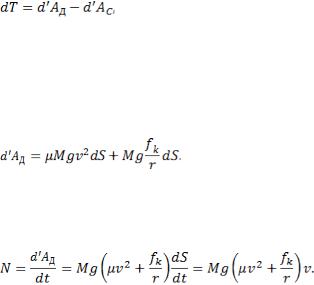
направлениям: . Конечно работу будет совершать только первая пара с моментом , где – угол между вектором и осью вращения z,

. (5)

1111111111111111111111111111111111111111111111111111111

http://www.teoretmeh.ru/dinamika2.htm

Пример 1. Автомобиль массы M движется прямолинейно по горизонтальной дороге со скоростью v. Коэффициент трения качения между колесами автомобиля и дорогой равен fk, радиус колес – r, сила аэродинамического сопротивления воздуха пропорциональна квадрату скорости: , где μ – коэффициент, зависящий от формы автомобиля. Определить мощность двигателя, передаваемую на оси ведущих колес, в установившемся режиме.

Решение.

В соответствии с теоремой об изменении кинетической энергии будем

иметь

где - элементарная работа движущей силы, - элементарная работа сил сопротивления движению. В установившемся режиме скорость v автомобиля постоянна и, следовательно, его кинетическая энергия не изменяется, т.е. dT=0. Это означает, что 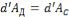. Раскроем правую часть полученного равенства:

Здесь dS – элементарное перемещение автомобиля. Тогда мощность, передаваемая двигателем на оси ведущих колес, будет равна

Таким образом, при движении с постоянной скоростью по горизонтальной дороге двигатель автомобиля развивает постоянную мощность; соответственно, топливо в баке расходуется равномерно.

76

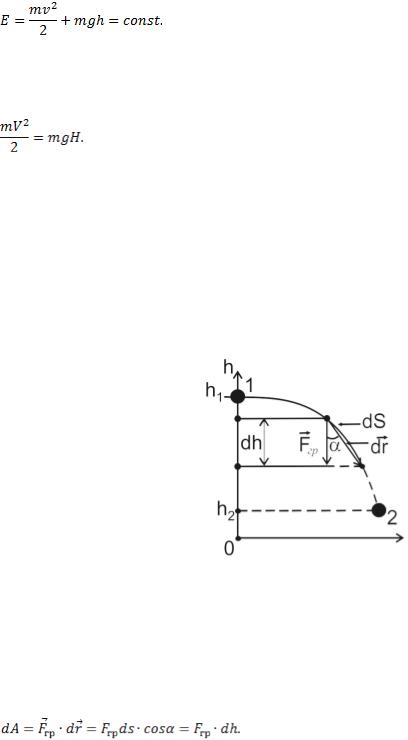
Пример 2. Стальной шарик сброшен с высоты H = 15 м без начальной скорости. Найти скорость шарика V в момент его удара о землю. Сопротивлением воздуха пренебречь.

Решение.

На шарик действует только сила тяжести, которая является потенциальной и ее потенциал явно от времени не зависит. Следовательно, в соответствии с (10), полная механическая энергия шарика при его движении будет постоянной

Так как в начальный момент времени шарик покоился и обладал только потенциальной энергией, то в момент удара о землю вся его начальная потенциальная энергия переходит в кинетическую энергию

Отсюда следует, что Результат решения этой задачи дает нам право утверждать, что скорость свободного падения тел не зависит от их массы.

Пример 3. Рассмотрим свободное падение камня массой m, брошенного в поле гравитации Земли из точки 1 в точку 2 (рис. 11).

Рис.11

Элементарная работа, совершаемая силой тяжести при перемещении камня, равна:

Полная работа на участке 1–2 находится как

77

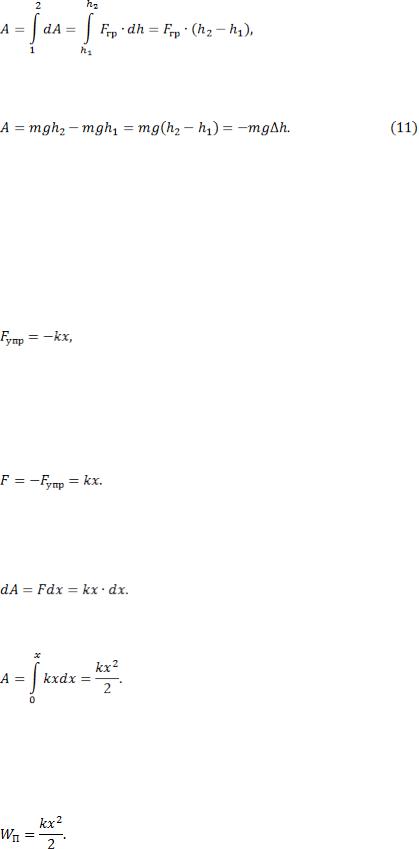
где Fгр = mg – сила тяжести; тогда получаем:

Из последнего выражения видно, что работа определяется только положением начальной и конечной точек траектории тела.

Пример 4. Найдем потенциальную энергию упруго деформированного тела (пружины). Известно, что сила упругости пропорциональна деформации x:

где k – коэффициент упругости; x – значение деформации; знак (–) указывает, что Fупр направлена в сторону, противоположную деформации.

Для преодоления силы упругости необходимо приложить силу:

Элементарная работа – работа, совершаемая при бесконечно малой деформации:

Полная работа найдется как

Работа в данном примере идет на увеличение потенциальной энергии пружины. Если при x = 0 Won = 0, то с = 0. Потенциальная энергия упругодеформированного тела равна

78

закону: Wр= -αx4, где α - положительная постоянная. Найти зависимость ускорения точки от координаты x.

Решение. Используя связь между силой и потенциальной энергией:

найдем зависимость силы от координаты x:

По второму закону Ньютона получим выражение для ускорения:

Если аналитически или графически задана зависимость потенциальной энергии от угла поворота при вращательном движении, то, применяя

соотношение , можно выразить момент силы, а также найти угловое ускорение

Пример 6. Вагон массой m = 20 т, двигаясь равнозамедленно с начальной скоростью v0 = 54 км/ч, под действием силы трения Fmp = 6 кН через некоторое время останавливается. Найти работу A сил трения и расстояние S, которое вагон пройдет до остановки.

Решение.

1) Работа А, совершаемая результирующей силой, может быть определена как мера изменения кинетической энергии материальной точки:

где Wk=mv2/2=0.

Отсюда A=-Wk0;

A=-2,25 МДж

2) Расстояние

79

Ответ: Работа сил трения равна -2,25 МДж, расстояние которое вагон пройдет до остановки 375 м.

http://k-a-t.ru/tex_mex/22-dinamika_6/index.shtml

80