теормех / ОТВЕТЫ ТЕОРМЕХ

, , . (171')

Теорема об изменении кинетического момента системы

Первая производная по времени от кинетического момента системы относительно какой-либо точки равна векторной сумме моментов внешних сил, действующих на систему, относительно той же точки.

, (172)

где – главный момент всех внешних сил системы.

Проецируя (172) на прямоугольные декартовы оси координат, получаем теоремы об изменении кинетического момента системы относительно этих осей координат, т. е.

, , . (172')

Законы сохранения кинетических моментов

1. Если главный момент внешних сил системы относительно точки

равен нулю, т. е. , то, согласно (79), кинетический момент системы относительно той же точки постоянен по модулю и направлению, т. е.

. (173)

Этот частный случай теоремы об изменении кинетического момента системы называют законом сохранения кинетического момента. В

проекциях на прямоугольные декартовы оси координат по этому закону

, , ,

где , , – постоянные величины.

111

2. Если сумма моментов всех внешних сил системы относительно

оси равна нулю, т.е. , то из (172') следует, что

. (174)

+Следовательно, кинетический момент системы относительно какой-либо координатной оси постоянен, если сумма моментов внешних сил относительно этой оси равна нулю, что, в частности,

наблюдается, когда внешние силы параллельны оси или пересекают ее. В частном случае для тела или системы тел, которые все вместе могут вращаться вокруг неподвижной оси, и если при этом

,

то

, или , (175)

где и – момент инерции системы тел и их угловая скорость

относительно оси вращения в произвольный момент времени ; и

– момент инерции тел и их угловая скорость в момент времени, выбранный за начальный.

Дифференциальное уравнение вращения твердого тела вокруг неподвижной оси

Из теоремы об изменении кинетического момента (172') следует дифференциальное уравнение вращения твердого тела вокруг неподвижной оси :

, (176)

где 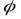– угол поворота тела.

Дифференциальное уравнение вращательного движения твердого тела в общем случае позволяет решать две основные задачи: по заданному вращению тела определять вращающий момент внешних

112

сил и по заданному вращательному моменту и начальным условиям находить вращение тела. При решении второй задачи для нахождения угла поворота приходится интегрировать дифференциальное уравнение вращательного движения. Методы его интегрирования полностью аналогичны рассмотренным методам интегрирования дифференциального уравнения прямолинейного движения точки.

Теорема об изменении количества движения системы.

113

114

115

117

Случай, когда система является абсолютно твердым телом.

Абсолютно твёрдое тело – материальный объект, расстояние между двумя точками на поверхности которого всегда остаётся постоянным. Это цело является ещё и абсолютно жёстким. Любое атт можно рассматривать как систему материальных точек. Мера механического воздействия одного материального объекта на 2-ой

– это сила.(н)

Абсолютно твёрдое тело — механическая система, обладающая только поступательными и вращательными степенями свободы.

119

24. Основы аналитической механики. Малое и действительное бесконечно малое перемещение точки. Возможное перемещение. Элементарная работа силы на возможном перемещении точки. Идеальные связи. Принцип возможных перемещений. Пример.

Возможными (или виртуальными)

перемещениями называются воображаемые бесконечно малые перемещения механической системы, допускаемые в данный момент времени наложенными на систему внешними и внутренними связями.

В отличие от действительных бесконечно малых перемещений, обозначаемых символом дифференциала d (например, ), возможные

перемещения обозначаются символом вариации ( ), хотя математически вариации и дифференциалы перемещений определяются

одинаково. Действительное перемещение какой-либо точки механической системы всегда одно, возможных перемещений у нее может быть больше, чем одно, в том числе - бесчисленное множество. В случае стационарных связей (то есть связей, свойства которых не зависят от времени, п. 3.9.2) действительное перемещение точки есть одно из ее возможных перемещений .

Например, для кривошипно-шатунного механизма (рис. 3.11) возможными перемещениями точки В (ползуна) являются два бесконечно малых перемещения вдоль горизонтальной направляющей – в одну или другую сторону. Действительное бесконечно малое перемещение - одно из них. Поскольку возможные перемещения являются бесконечно малыми, то криволинейные перемещения точек (например, точки А кривошипа ОА) по дуге окружности можно заменить

120