теормех / ОТВЕТЫ ТЕОРМЕХ 4

41

42

14. Кинематика твердого тела. Поступательное движение твердого тела.

Теорема о скоростях точек поступательно движущегося твердого тела. Вращательное движение твердого тела вокруг неподвижной оси. Угловая

скорость и угловое ускорение. Линейные скорости и ускорения точек вращающегося твердого тела. Примеры. Со стр 95

https://5iz5.ucoz.ru/publ/dlja_vuzov/mekhanika/reshebnik_gdz_onlajn_sbornik_zadach _po_teoreticheskoj_mekhanike_meshherskij_kinematika/71-1-0-125

43

Кинематика твёрдого тела (от др.-греч. — движение) — раздел кинематики, изучающий движение абсолютно твёрдого тела, не вдаваясь в вызывающие его причины.

44

Поступательное движение твердого тела – это такое движение, при котором любая прямая, проведенная в этом теле, перемещается, оставаясь параллельной самой себе

При поступательном движении все точки тела имеют в каждый момент времени одинаковые по модулю и направлению скорости и ускорения, их траектории конгруэнтны, а разность радиус-векторов любых двух точек равна вектору, который зависит от положений сравниваемых точек, но не зависит от времени.

При поступательном движении угловая скорость и угловое ускорение равны нулю:

. Тогда формулы Эйлера принимают вид:

.

Вращательное движение вокруг неподвижной оси

Определение

45

Вращательное движение твердого тела вокруг неподвижной оси

– это такое движение, при котором неподвижны все точки тела, лежащие на некоторой прямой, которая называется осью

вращения.

При вращении все точки тела движутся в плоскостях, перпендикулярных оси вращения. Их траекториями являются окружности с центром на оси вращения. Положение тела

определяется углом поворота φ относительно произвольным образом выбранного нулевого положения. Зависимость угла поворота от времени определяет закон вращательного движения или, что тоже самое, уравнение вращательного движения. Единицей измерения угла поворота является радиан, который считается безразмерной величиной.

180° = π радиан 1 радиан = 180/π = 57,29578°.

Угловая скорость и ускорение

Угловая скорость

– это производная угла поворота по времени:

.

Она определяет быстроту изменения угла φ.

Вектор угловой скорости параллелен оси вращения. Его направление определяется правилом правого винта. Он не имеет точки приложения и применим ко всем точкам твердого тела, то есть ко всему телу в целом. Однако, для наглядности, вектор угловой скорости изображают на оси вращения.

Единицей измерения угловой скорости является 1 рад/с или, что тоже самое, 1/с = с–1. В технике встречаются другие единицы измерения.

Пусть n – число оборотов в минуту. Тогда 1 оборот = 2π радиан; 1 минута = 60 с; ;

n об/мин = n·2π/60 рад/с. Тогда

.

Угловое ускорение

46

– это производная угловой скорости по времени:

.

Единицей измерения углового ускорения является рад/с2 или, что тоже самое, с–2.

Вектор углового ускорения также параллелен оси вращения. При ускоренном вращении он совпадает с направлением угловой скорости. При замедленном – имеет противоположное направление.

Теорема. При поступательном движении твердого тела все его точки описывают одинаковые траектории и в каждый данный момент

имеют равные по модулю и направлению скорости и ускорения. + Доказательство. Проведем через две точки и, поступательно движущегося тела отрезок и

рассмотрим движение этого отрезка в положении.

47

15. Плоское движение твердого тела. Скорости точек плоской фигуры. Ускорения точек плоской фигуры.

http://botvaproject.ru/library/%D0%9F%D0%BB%D0%BE%D1%81%D0%BA%D 0%BE%D0%B5_%D0%B4%D0%B2%D0%B8%D0%B6%D0%B5%D 0%BD%D0%B8%D0%B5.pdf

Плоским движением твердого тела называется такое его движение, при котором каждая точка тела движется в

плоскости, параллельной некоторой неподвижной плоскости

Рассмотрим методы, с помощью которых можно определить скорости точек тела, совершающего плоское движение.

+1. Метод полюса. Этот метод основывается на полученном разложении плоского движения на поступательное и вращательное. Скорость любой точки плоской фигуры можно представить в виде двух составляющих: поступательной, со скоростью равной скорости произвольно выбранной точки – полюса, и вращательной вокруг этого полюса

Теорема: ускорение любой точки плоской фигуры равно геометрической сумме ускорения полюса и ускорения этой точки во вращательном движении фигуры вокруг полюса.

Ускорения точек плоской фигуры

Формула распределения ускорений при плоском движении тела имеет вид:

где 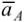- ускорение полюса, точки , в поступательном движении;

48

- относительное ускорение точки в ее вращательном движении вместе с телом вокруг полюса ;

- ускорение любой точки тела.

Ускорение любой точки плоской фигуры равно геометрической сумме ускорения точки, которую выбрано за полюс, и ускорения точки при его вращении вместе с телом вокруг этого полюса.

Графическое определение ускорения точки выполняется следующим образом (рис.4.16):

Из точки откладывают вектор , который равен ускорению полюса ;

Под углом к проводят вектор , отклоненный в сторону углового ускорения , причем

Модуль и направление ускорения определяется диагональю параллелограмма, который построен на векторах и как на сторонах.

Вычисление величины ускорения точки с помощью рассматриваемого параллелограмма затрудняет расчеты,

49

поскольку предварительно надо определить угол между векторами и .

Учитывая, что представляет собой относительное ускорение точки в ее относительном вращательном

движении вокруг полюса , то это ускорение можно разложить на относительную тангенциальную (касательную) и относительную нормальную (центростремительную) составляющие:

где

Вектор направлен перпендикулярно в сторону углового ускорения, а вектор всегда направлен от точки к выбранному полюсу (рис.4.17).

Тогда уравнение (4.10) примет вид:

Если точка , которая выбрана за полюс поступательного движения, движется не прямолинейно, то ее ускорение, в

свою очередь, тоже можно разложить на тангенциальную и нормальную составляющие:

50