теормех / ОТВЕТЫ ТЕОРМЕХ 4

21

22

9. Понятие вектора. Переменные и постоянные векторы. Орты. Разложение

вектора по координатным осям. Скалярное и векторное произведение двух векторов. Производная вектора по скалярному аргументу. Направление производной. Свойства производной.

Вектор это направленный отрезок, который характеризуется длиной и направлением.

Вектор считается постоянным, если с течением времени он не меняет свое направления и модуль.

Вектор считается переменным, если с течением времени он изменяет свой модуль или направление или одновременно и то и другое.

Вектор, изменяющий с течением времени только свое направление,

называется переменным вектором постоянного модуля.

23

24

Рассмотрим прямоугольную систему координат в пространстве Оxyz.

На каждой из осей выберем единичный вектор, направление которого совпадает с положительным направлением оси. Так, на оси

Ох возьмем единичный вектор , на оси Оу – , а на оси Оz – ;

.

Эти три единичных взаимно перпендикулярных вектора называют ортами. Так как орты не компланарны, то

они образуют базис, который называется декартовым ортогональным базисом. Декартов базис называется правым, если

направление кратчайшего вращения от вектора к вектору (при

условии, что смотрят с конца вектора ) противоположно направлению вращения часовой стрелки. В противном случае базис

называется левым.

Рассмотрим некоторый вектор в пространстве.

С помощью параллельного переноса отложим

этот вектор от начала координат О, т. е. . Проведем через точку М три плоскости перпендикулярные осям координат Ох, Оу, Oz. По правилу сложения векторов:

. ( )

Векторы 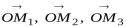являются проекциями вектора на оси координат, следовательно, по определению имеем:

25

Обозначая проекции вектора на оси Ох, Оу, Oz соответственно через х, Y, z и подставив в формулу (1) получим

.

+Данная формула называется разложением вектора на составляющие по координатным осям. Это равенство для краткости будем записывать следующим образом:

.

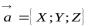26

27

28

29

10. Производная от переменного вектора постоянного модуля.

Производная от переменного вектора постоянного модуля по скалярному аргументу

Напомним, что вектор, изменяющий с течением времени t свое направление и не изменяющий свой модуль называется переменным вектором постоянного модуля.

30