теормех / ОТВЕТЫ ТЕОРМЕХ 4

121

122

124

Случай, когда система является абсолютно твердым телом.

Абсолютно твёрдое тело – материальный объект, расстояние между двумя точками на поверхности которого всегда остаётся постоянным. Это цело является ещё и абсолютно жёстким. Любое атт можно рассматривать как систему материальных точек. Мера механического воздействия одного материального объекта на 2-ой

– это сила.(н)

Абсолютно твёрдое тело — механическая система, обладающая только поступательными и вращательными степенями свободы.

126

24. Основы аналитической механики. Малое и действительное бесконечно малое перемещение точки. Возможное перемещение. Элементарная работа силы на возможном перемещении точки. Идеальные связи. Принцип возможных перемещений. Пример.

Возможными (или виртуальными)

перемещениями называются воображаемые бесконечно малые перемещения механической системы, допускаемые в данный момент времени наложенными на систему внешними и внутренними связями.

В отличие от действительных бесконечно малых перемещений, обозначаемых символом дифференциала d (например, ), возможные

перемещения обозначаются символом вариаци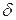и ( ), хотя математически вариации и дифференциалы перемещений определяются

одинаково. Действительное перемещение какой-либо точки механической системы всегда одно, возможных перемещений у нее может быть больше, чем одно, в том числе - бесчисленное множество. В случае стационарных связей (то есть связей, свойства которых не зависят от времени, п. 3.9.2) действительное перемещение точки есть одно из ее возможных перемещений .

Например, для кривошипно-шатунного механизма (рис. 3.11) возможными перемещениями точки В (ползуна) являются два бесконечно малых перемещения вдоль горизонтальной направляющей – в одну или другую сторону. Действительное бесконечно малое перемещение - одно из них. Поскольку возможные перемещения являются бесконечно малыми, то криволинейные перемещения точек (например, точки А кривошипа ОА) по дуге окружности можно заменить

127

прямолинейными перемещениями по касательной к траектории точки: ( на рис. 3.11).

Возможные перемещения системы ограничены наложенными на нее связями, поэтому для определения положения точек системы нет необходимости знать координаты всех точек. Например, положение всех звеньев и точек кривошипношатунного механизма (рис. 3.11) вполне определяется заданием только одного угла поворота кривошипа. Координаты всех точек этого механизма могут быть выражены в функции от одной независимой переменной – угла . Механическую систему, положение которой однозначно определяется заданием одним геометрическим параметром (линейной или угловой координатой), называют системой с одной степенью свободы.

Для определения положения точки в пространстве надо задать не одну, а три координаты – например, 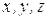в прямоугольной декартовой системе координат. Независиые геометрические параметры (как правило, линейные и угловые координаты), заданием которых однозначно определяется положение механической системы, называются обобщенными координатами механической системы. Число обобщенных координат называется числом степеней свободы механической системы. Число независимых между собой возможных перемещений равно числу степеней свободы механической системы.

Основы аналитической механики - это раздел теоретической механики, в

котором изучение равновесия и движения механических систем основано на дифференциальных и интегральных принципах механики

128

Возможные перемещения

Для одной точки возможным (виртуальным) перемещением называется такое бесконечно милое (элементарное) мысленное перемещение, которое допускается в рассматриваемый момент времени наложенными на точку связями. Для возможного перемещения не требуется времени на его совершение. Это мысленное перемещение, которое могла бы совершить точка при наложенных на нее связях в рассматриваемый момент времени. В отличие от элементарного (бесконечно малого) действительного перемещения точки , которое совершает точка за время под действием приложенных сил при заданных начальных условиях и наложенных связях, возможное перемещение определяется только связями в данный момент. Проекции возможного перемещения на оси координат, или вариации координат, обозначают ,,, а проекции элементарного действительного перемещения на оси координат, или дифференциалы координат при изменении времени на обозначают , , .

Возможных перемещений у точки в момент времени 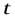бесконечно много. Если, например, точка движется по поверхности, все допускаемые связью (поверхностью) возможные перемещения как отрезки бесконечно малой длины расположатся в касательной плоскости к поверхности в точке, в которой находится рассматриваемая материальная точка в данный момент времени.

Возможное перемещение , как и действительное , является вектором и потому всегда изображается направленным прямолинейным отрезком.

Возможным перемещением системы называют любую совокупность возможных перемещений точек системы. В общем случае система может иметь несколько и даже бесконечно много возможных перемещений. Вследствие уравнений связей, наложенных на систему, не все возможные перемещения являются независимыми. Число независимых возможных перемещений называют числом степеней свободы системы.

Свободная точка имеет три степени свободы. В этом случае возможные перемещения (вариации) ,, (или выраженные

129

через вариации каких-либо других координат) являются независимыми.

3.6.3. Элементарная работа силы на возможном перемещении. Идеальные связи

Элементарную работу силы на возможном перемещении ее точки приложения вычисляют по обычным формулам для элементарной работы, т.е. , и другим формулам для элементарной работы. Для механической системы, состоящей из 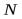точек, к которым приложены силы, элементарная работа этих сил на каком-либо возможном перемещении системы соответственно выразится так

. (219)

Элементарная работа сил при этом зависит от выбора возможного перемещения системы.

Обозначим силы реакций связей для точек системы . Тогдасвязи системы называются идеальными, если для любого возможного перемещения системы выполняется условие

. (220)

Условие (220) является определением идеальных связей. Важно отметить, что это условие должно выполняться для всех возможных перемещений системы. При этом вся совокупность связей является идеальной. Может быть идеальной каждая из связей в отдельности. Приведем примеры идеальных связей.

1.В абсолютно твердом теле точки связаны идеальными связями. Силами реакций связей в этом случае являются внутренние силы, для которых было доказано, что сумма элементарных работ этих сил на любых элементарных перемещениях точек тела равна нулю.

2.Абсолютно гладкая поверхность, или абсолютно гладкая линия,

является идеальной связью для точки. Возможные перемещения точки с такими связями направлены по касательным к поверхности или линии. Силы реакции в этих случаях направлены по нормалям к ним, т. е. перпендикулярны силам. Так, например, все шарниры (поверхности) без трения, подвижные и неподвижные, являются связями, идеальными для тел, соединенных такими связями.

130