теормех / ОТВЕТЫ ТЕОРМЕХ 4

Сила , как видим, стремится вернуть точку в равновесное положение О, где

Рис. 3.7

Найдём закон движения точки С, составим дифференциальные уравнения движения

(30)

Деля обе части на m и вводя обозначение

приведём уравнение к виду

(31)

Уравнение (31) представляет собой дифференциальное уравнение свободных колебаний при отсутствии сопротивления. Решение этого однородного дифференциального уравнения ищут в виде . Полагая в уравнении (31) , получим для определения n так называемое характеристическое уравнение, имеющее в данном случае вид: .

Общее решение уравнения (31) имеет вид:

(32)

Если вместо постоянных и ввести постоянные и , такие, что , , то получим:

или

(33)

Скорость точки в рассматриваемом движении

(34)

91

Колебания, совершаемые точкой по закону (32), называется гармоническими колебаниями. График их при

Рис. 3.8

Рассмотрим точку B, равномерно на окружности из скольжения , определяется углом . Пусть постоянная угловая скорость вращение радиусов равна . Тогда в произвольный

момент t угол и легко увидеть, что проекция М точки В на диаметр движется по закону . Величина а – называется амплитудой колебаний - фазой колебаний. Величина определяет

фазу начала колебаний (начальная

Рис. 3.9 фаза). Величина называется круговой частотой

колебаний.

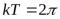Промежуток времени Т в течении которого точка совершает одно полное колебание, называется периодом колебаний. По истечении периода фаза изменяется на . Следовательно откуда

(35)

Величина - частота колебаний.

Отметим, что свободные колебания при отсутствии сопротивления обладают следующими свойствами:

1.амплитуда и начальная фаза колебаний зависят от начальных условий

2.частота k, а следовательно и период Т от начальных условий не зависят.

92

Рассмотрим влияние постоянной силы на свободные колебания точки.

Пусть на точку М кроме восстанавливающей силы F действует постоянная по модулю и направлению сила Р. Величина силы F по прежнему пропорциональна расстоянию от центра О, т.е. .

Очевидно, что в этом случае положением точки М будет центр , отстраненной от оси О на расстояние , которое определяется равенством

или (36)

- статическое отклонение

точки.

Рис. 3.10

Примем за начало отсчёта, тогда будет , и

учитывая будем иметь или , что полностью совпадает с уравнением (31).

Постоянная сила Р не изменяет характера колебаний, совершаемой точкой под действием восстанавливающей силы F, а только смещает центр этих колебаний в сторону действия силы Р на величину статического отклонения .

+Из (36) и (30) имеем

Тогда равенство (35) даст (37)

В частности, если Р – сила тяжести , то формула (34) имеет вид:

(37/)

93

Влияние постоянной силы на свободные колебания.

Вынужденные колебания материальной точки (диф. уравнение и структура его решения).

Вынужденные колебания совершает материальная точка, на которую наряду с восстанавливающей силой действует периодически изменяющаяся сила, называемая возмущающей силой (рис. 3.21)

Рис. 3.21

,

+где Н – максимальный модуль или амплитуда возмущающей силы; р - частота изменения возмущающей силы, равная числу полных циклов изменения возмущающей силы за 2π с; pt+δ - фаза изменения возмущающей силы: δ- начальная фаза изменения возмущающей силы.

Период изменения возмущающей силы определяется по ее частоте:

94

.

Дифференциальное уравнение вынужденных колебаний имеет вид:

, (3.15)

Общее решение уравнения (3.15) складывается из общего решения однородного уравнения и частного решения данного уравнения

(3.15):

.

Однородное уравнение имеет общее решение:

.

Частное решение уравнения (3.15):

.

Общее решение уравнения (3.15) получит вид

или

.

95

Случай различных частот собственных колебаний и вынужденных колебаний.

Амплитуда вынужденных колебаний малой частоты (при р<k) имеет вид

.

Амплитуда вынужденных колебаний большой частоты (при р>k) имеет вид

.

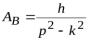Введем статическое отклонение точки М от начала координат О под действием постоянной силы Н (рис. 3.22).

Величина определяется из условия равновесия сил = :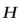

,

откуда

.

Рис. 3.22

Отношение η амплитуды вынужденных колебаний AВ к величине называется коэффициентом динамичности:

при p<k

при p>k

96

Вынужденные колебания материальной точки с учетом сопротивления

Дифференциальное уравнение движения материальной точки М, совершающей прямолинейное движение под действием восстанавливающей силы , возмущающей силы , изменяющейся по гармоническому закону (рис. 3.23), и силы сопротивления имеет вид

или

, (а)

где

.

Рис. 3.23

Общее решение уравнения (а) состоит из общего решения ypaвнения и частного решения данного уравнения (а): . Частное решение уравнения (а) имеет вид

,

где - амплитуда вынужденных колебаний с учетом сопротивления, определяется по зависимости

,

- величина сдвига фазы вынужденных колебаний по отношению к фазе возмущающей силы:

97

;

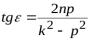Общее решение уравнения (а) в зависимости от соотношения величин k и n имеет вид:

1)при n < k

2)при n > k

3)при n = k

.

Величины A и β в уравнениях, а также С1 и С2 в уравнении являются постоянными интегрирования и определяются по начальным условиям движения.

+Влияние сопротивления на вынужденные колебания материальной точки выражается в сдвиге фазы колебаний относительно фазы возмущающей силы и в уменьшении амплитуды колебаний по мере увеличения сопротивления.

111111111111111111111

Затухающие колебания (движения) материальной точки –

движение материальной точки, которое происходит

при наличии восстанавливающей силы и силы сопротивления движению.

98

Зависимость силы сопротивления движению от смещения или скорости определяется физической природы среды или связи, препятствующей движению.

Наиболее простой зависимостью является линейная зависимость

от скорости (вязкое сопротивление):

a - коэффициент вязкости

Учтем еще, что - проекция силы упругости. Тогда дифференциальное уравнение движения

запишется или, после преобразований к каноническому виду,

.

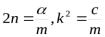Характеристическое уравнение имеет корни

+Общее решение данного дифференциального уравнения имеет различный вид в зависимости от значений корней:

1. n < k – случай малого вязкого сопротивления: -

корни комплексные, различные.

В этом случае решение имеет вид

или

То есть имеют место затухающие колебания.

Частота колебаний:

99

.

Период

Основное влияние силы вязкого сопротивления – уменьшение амплитуды колебаний с течением времени.

2. n > k – случай большого вязкого сопротивления:

- корни действительные, различные Решение имеет вид или Это функции апериодические

3. n = k : - корни действительные, кратные.

Решение . Эти функции также апериодические:

Типичный вид графиков решений в случаях 2 и 3

100