теормех / ОТВЕТЫ ТЕОРМЕХ 1

Ответ: Работа сил трения равна -2,25 МДж, расстояние которое вагон пройдет до остановки 375 м.

http://k-a-t.ru/tex_mex/22-dinamika_6/index.shtml

81

22. Колебательное движение материальной точки. Линейная сила упругости. Коэффициент жесткости. Статическое отклонение. Свободные

прямолинейные колебания материальной точки. Влияние постоянной силы на свободные колебания. Вынужденные колебания материальной точки (диф. уравнение и структура его решения). Случай различных частот собственных колебаний и вынужденных колебаний. Случай равенства частот собственных колебаний и вынужденных колебаний. Резонанс.

Колебательное движение материальной точки

Колебательное движение материальной точки происходит в случае, когда на точку, отклоненную от состояния покоя, действует сила, старающаяся возвратить точку в исходное положения.

Сила, старающаяся возвратить материальную точку в положение равновесия,

называется восстанавливающей силой.

Колебательным движением называется движение, которое характеризуется многократным прохождением положения равновесия.

Виды колебательного движения материальной точки:

1.свободные колебания, создающиеся только под действием восстанавливающей силы;

2.затухающие колебания − свободные колебания, создающиеся под действием восстанавливающей силы и силы сопротивления среды;

3.вынужденные колебания, создающиеся под действием восстанавливающей силы и силы периодического характера, называемой возмущающей силой;

4.вынужденные колебания, создающиеся под действием восстанавливающей силы, возмущающей силы и силы сопротивления среды.

Линейная сила упругости. Коэффициент жесткости.

Функция называется характеристикой восстанавливающей силы.

Если характеристикой восстанавливающей силы служит линейная функция

то восстанавливающая сила называется линейной, а колебания под действием линейной восстанавливающей силы — линейными колебаниями. Во всех остальных случаях восстанавливающая сила и соответствующие колебания называются нелинейными. В математическом отношении нелинейные колебания много сложнее линейных колебаний и далее рассматриваться не будут.

82

Одним из примеров, когда возникает восстанавливающая сила, служит тело, закрепленное к концу цилиндрической пружины, другой конец которой неподвижен

(рис. 9). Восстанавливающей силой является упругая сила пружины ,

пропорциональная деформации (закон Гука): . Коэффициент с в этом случае называется жесткостью пружины. К возникновению восстанавливающей силы приводит «игра» силы тяжести и архимедовой выталкивающей силы плавающего тела, например понтона (рис. 10). Левый рисунок изображает понтон в положении равновесия; средний и правый рисунки — смещенное положение понтона (соответственно вниз и вверх); восстанавливающей силой служит сумма веса

понтона и архимедовой силы , показанная на рисунке сдвоенной линией.

Статическое отклонение.

83

Свободные прямолинейные колебания материальной точки.

Прямолинейные колебания материальной точки – колебательное движение материальной точки - движение, происходящее при условии: имеется восстанавливающая сила, стремящаяся вернуть точку в положение равновесия при любом отклонении ее из этого положения.

Свободные колебания – происходят под действием только восстанавливающей силы.

Выберем систему координат с центром в положении равновесия (точке O)

и запишем диф.уравнение движения точки в проекции на ось x : .

Свободные колебания без учёта сил сопротивления.

Рассмотрим точку М, движущуюся под действием одной только восстанавливающей силы F, направленной к неподвижному центру и

пропорциональной расстоянию от этого центру.

Проекции силы на ось Ox будет равна

84

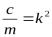
Сила , как видим, стремится вернуть точку в равновесное положение О, где

Рис. 3.7

Найдём закон движения точки С, составим дифференциальные уравнения движения

(30)

Деля обе части на m и вводя обозначение

приведём уравнение к виду

(31)

Уравнение (31) представляет собой дифференциальное уравнение свободных колебаний при отсутствии сопротивления. Решение этого однородного дифференциального уравнения ищут в виде 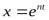. Полагая в уравнении (31) , получим для определения n так называемое характеристическое уравнение, имеющее в данном случае вид: .

Общее решение уравнения (31) имеет вид:

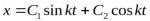(32)

Если вместо постоянных и ввести постоянные и , такие, что , , 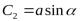то получим:

или

(33)

Скорость точки в рассматриваемом движении

(34)

85

Колебания, совершаемые точкой по закону (32), называется гармоническими колебаниями. График их при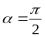

Рис. 3.8

Рассмотрим точку B, равномерно на окружности из скольжения , определяется углом . Пусть постоянная угловая скорость вращение радиусов равна . Тогда в произвольный

момент t угол и легко увидеть, что проекция М точки В на диаметр движется по закону . Величина а – называется амплитудой колебаний - фазой колебаний. Величина определяет

фазу начала колебаний (начальная

Рис. 3.9 фаза). Величина называется круговой частотой

колебаний.

Промежуток времени Т в течении которого точка совершает одно полное колебание, называется периодом колебаний. По истечении периода фаза изменяется на . Следовательно откуда

(35)

Величина - частота колебаний.

Отметим, что свободные колебания при отсутствии сопротивления обладают следующими свойствами:

1.амплитуда и начальная фаза колебаний зависят от начальных условий

2.частота k, а следовательно и период Т от начальных условий не зависят.

86

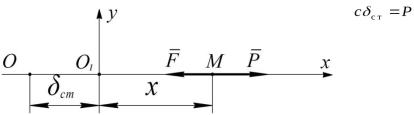
Рассмотрим влияние постоянной силы на свободные колебания точки.

Пусть на точку М кроме восстанавливающей силы F действует постоянная по модулю и направлению сила Р. Величина силы F по прежнему пропорциональна расстоянию от центра О, т.е. .

Очевидно, что в этом случае положением точки М будет центр , отстраненной от оси О на расстояние , которое определяется равенством

или (36)

- статическое отклонение

точки.

Рис. 3.10

Примем за начало отсчёта, тогда будет , и

учитывая будем иметь или , что полностью совпадает с уравнением (31).

Постоянная сила Р не изменяет характера колебаний, совершаемой точкой под действием восстанавливающей силы F, а только смещает центр этих колебаний в сторону действия силы Р на величину статического отклонения .

+Из (36) и (30) имеем

Тогда равенство (35) даст (37)

В частности, если Р – сила тяжести , то формула (34) имеет вид:

(37/)

87

Влияние постоянной силы на свободные колебания.

Вынужденные колебания материальной точки (диф. уравнение и структура его решения).

Вынужденные колебания совершает материальная точка, на которую наряду с восстанавливающей силой действует периодически изменяющаяся сила, называемая возмущающей силой (рис. 3.21)

Рис. 3.21

,

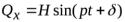+где Н – максимальный модуль или амплитуда возмущающей силы; р - частота изменения возмущающей силы, равная числу полных циклов изменения возмущающей силы за 2π с; pt+δ - фаза изменения возмущающей силы: δ- начальная фаза изменения возмущающей силы.

Период изменения возмущающей силы определяется по ее частоте:

88

.

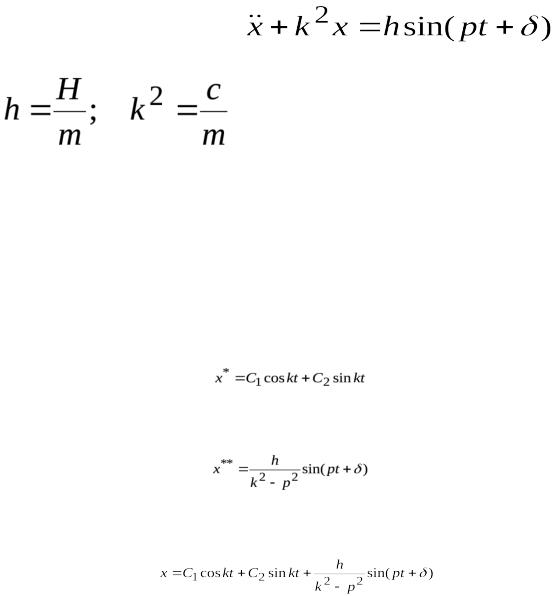
Дифференциальное уравнение вынужденных колебаний имеет вид:

, (3.15)

Общее решение уравнения (3.15) складывается из общего решения однородного уравнения и частного решения данного уравнения

(3.15):

.

Однородное уравнение имеет общее решение:

.

Частное решение уравнения (3.15):

.

Общее решение уравнения (3.15) получит вид

или

.

89

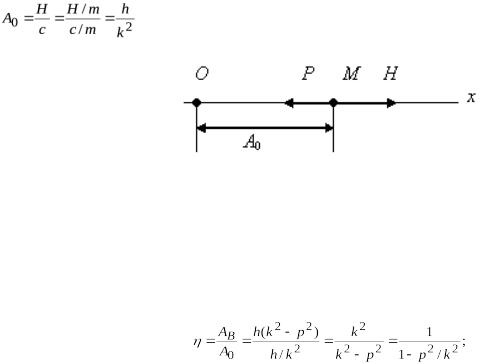
Случай различных частот собственных колебаний и вынужденных колебаний.

Амплитуда вынужденных колебаний малой частоты (при р<k) имеет вид

.

Амплитуда вынужденных колебаний большой частоты (при р>k) имеет вид

.

Введем статическое отклонение точки М от начала координат О под действием постоянной силы Н (рис. 3.22).

Величина определяется из условия равновесия сил = :

,

откуда

.

Рис. 3.22

Отношение η амплитуды вынужденных колебаний AВ к величине называется коэффициентом динамичности:

при p<k

при p>k

90