теормех / ОТВЕТЫ ТЕОРМЕХ 1

Поскольку прямые и пересекаются в точке , к которой можно приложить и заданную силу , то при решении задачи надо рассматривать равновесие точки .

Таким образом, на объект равновесия, точку (рис.2.6), действуют силы

натяжения ветки нити ; натяжения ветки нити ; весы тела . (Вес тел и учитывать не надо, поскольку они приложены не к объекту равновесия точки ).

Составим уравнение равновесия. Для этого, выберем систему

координат с началом в точке , спроецируем силы на оси и составим уравнение равновесия.

Для проекций на ось достанем:

Знак проекции - плюс, поскольку она направлена по положительному направлению оси . Знак проекции - минус, поскольку она направлена

по отрицательному направлению оси . Проекция силы на ось равна нулю.

Сумма проекций всех сил на ось равна:

Проекции сил и имеют знак плюс, поскольку направлены по

положительному направлению оси . Проекция силы имеет знак минус, поскольку направлена по отрицательному направлению оси.

С учетом численных значений тригонометрических функций и величины , уравнения примут вид:

Найдя из первого уравнения:

11

и подставив во второе, получим:

Ответ:

Пример.

Груз в виде шара подвешен на нити, как указано на рис.С.16.

Нить составляет со стенкой угол α. Вес груза равен P . Определить силу натяжения нити T и силу давления груза на вертикальную стенку N .

Решение.

Из рисунка видно, что силы T T→, N N→ и P P→ образуют сходящуюся систему сил. Тогда из условия равновесия следует, что

{Rx=N−Tx=0Ry=−P+Ty=0

{Rx=N−Tx=0Ry=−P+Ty=0

Где Tx=Tsinα,Ty=TcosαTx=Tsin α,Ty=Tcos α

12

4. Теорема о трех силах. Примеры.

Теорема. Если свободное абсолютно твердое тело находится в равновесии под действием трех непараллельных сил, лежащих на одной плоскости, то линии действия этих сил пересекаются в одной точке.

Доказательство.

Пусть на абсолютно твердое тело, находящееся в равновесии действуют три непараллельные силы F 1F→1, F 2F→2 и F 3F→3 как указано на рис.

С.17а.

В соответствие со следствием аксиомы №2 силы F 1F→1 и F 2F→2 являются скользящими векторами и их можно перенести вдоль линии действия в точку их пересечения OO. Теперь силы

F 1F→1 и F 2F→2 приложены к одной точке и в соответствие с аксиомой №3 их можно сложить R =F 1+F 2R→=F→1+F→2.

Теперь, как следует из рис.С.17б тело находится в равновесии под действием системы состоящей из двух сил {F 3,R }{F→3,R→} и в соответствие с аксиомой №1 эти силы действуют вдоль одной прямой. Следовательно, линии действия сил F 1F→1 , F 2F→2 и F 3F→3 имеют общую точку пересечения, точку OO и образуют сходящуюся систему сил.

Пример.

Стержень ABAB в точке AA опирается на неподвижный шарнир, а в точке CC на выступ (рис.С.18).

13

Определить направления реакций в опорах (точках AA и CC).

Решение.

Решение приведено графически на рис.С.19.

14

5. Связи. Реакции связей. Основные типы реакций связей. Примеры.

По определению, тело, которое может совершать из данного по ложения любые перемещения в пространство, называется свободным (например, воздушный шар в воздухе). Тело, перемещениям кото рого в пространстве препятствуют какие-нибудь другие, скреплен ные или соприкасающиеся с ним, тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, называют связью.

Связями будем называть все тела, которые ограничивают перемещение данного тела.

Сила, с которой данная связь действует на тело, называется реакцией связи.

1. Гладкая поверхность.

Реакция гладкой поверхности перпендикулярна этой поверхности.

2. Невесомый стержень.

Реакция стержня всегда направлена вдоль его оси. Стержень может работать и на сжатие и на растяжение.

3. Неподвижный цилиндрический шарнир.

Как правило, направление реакцииRA заранее не известно, поэтому ее раскладывают по двум известным направлениям, например, по направлению координатных осей.

4. Подвижный цилиндрический шарнир.

направления (понятие момента силы будет рассмотрено позже). 6. Скользящая заделка.

15

+Реакция включает силу, перпендикулярную оси заделки, и реактивный момент.

Пример.

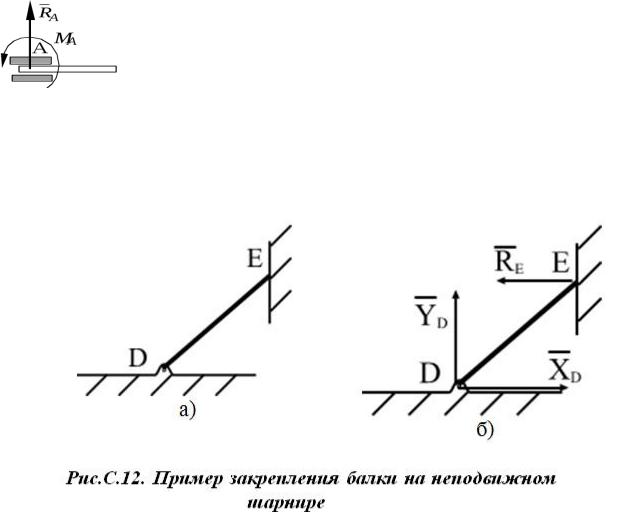
Брус DE закреплен в точке D неподвижным шарниром, а в точке Е опирается на гладкую поверхность стены (рис.С.12а).

Для бруса DE связями служат два тела: неподвижный шарнир D и гладкая поверхность стены.

Раскладываем реакцию неподвижного шарнира на две составляющие

X D→D и Y D→D и показываем на чертеже предполагаемые направления этих составляющих.

Реакция гладкой стены приложена в точке Е касания балки и стены и направлена по нормали к стене (рис.С.12б).

На рис.С.13 приведен также пример использования опирания на неподвижный шарнир и гладкий выступ.

16

17

6. Система параллельных сил. Сумма параллельных сил. Определение центра тяжести тел. Момент силы относительно точки. Теорема Вариньона.

Система сил, в которой векторы сил имеют параллельные линии действия, является параллельной системой сил.

Центр тяжести–центр приложенияравнодействующей сил тяготения ( материального тела. При определении положения центра тя используются гипотезы : 1. Линии действия сил тяготения отдельным частицам тела, параллельны (рассматриваемые т размеры многоньшиеме радиуса Земли и углом между линиями де тяготения частиц тел можно пренебречь) ; 2. Ускорение с const ( высота рассматриваемых тел много меньше радиуса изменением величины ускорения свободного паденияеламожнопо выс пренебречь) 3. Рассматриваемые–однородныетела (нет включений материалов с другой плотностью) и сплошные (нет пустот) гипотез при определении положения центра тяжести можно формулы для определения положенияапараллельныхцентр силG –: где силы тяжести элементарных объемов.

Сложение параллельных–Сложениесил двух параллельных сил подр рассмотрено в демонстрационной программе автора по теор ” на сайте МИИТа. Посмотреть…результат). Основной–две параллельные и направленные в одну сторону силы приводятся– к одной сил равнодействующей, приложенной в точке, делящей прямую н обратно пропорциональные величинам сил.

18

Момент силы относительно центра (точки)

Моментом силы F относительно центра О (m0(F)) (рис. 3.1) называется величина, равная произведению модуля силы на длину плеча. Момент силы величина векторная

В скалярном виде: m0(F) = F*h.

Знак (+) – если сила вращает тело против часовой стрелки.

Знак (-) – если сила вращает тело по часовой

стрелке.

Рис. 3.1

Момент силы измеряется в (Нм).

В векторной форме: m0(F) = r F.

Тогда модуль момента силы будет: m0(F) =

r*Fsin .

Вектор момента силы перпендикулярен плоскости , в которой лежат вектора r и F (рис. 3.2).

Теорема Вариньона о моменте равнодействующей

Момент равнодействующей плоской системы сходящихся сил относительно любого центра равен алгебраической сумме моментов слагаемых сил относительно того же центра (рис. 3.4).

m0(R) = m0(Fn)

направлена в одну и ту же сторону. Линия действия равнодействующей проходит между точками приложения слагаемых сил на расстоянии от этих точек, обратно пропорциональных силам.

19

7. Пара сил. Вычисление момента пары сил. Теорема об эквивалентности пары сил. Свойства пары сил.

Парой сил называется система двух, равных по модулю, параллельных и направленных в противоположные стороны сил, действующих на абсолютно твердое тело.

Вычисление алгебраического момента пары сил. Для вычисления алгебраического момента пары сил, удобно воспользоваться результатом следующей теоремы.

Теорема. Алгебраическая сумма моментов сил, составляющих пару, относительно любого центра, лежащего в плоскости действия пары сил не зависит от выбора этого центра. Момент пары сил равен произведению одной из сил, составляющих пару на плечо пары.

Теорема. Две пары сил, лежащие в одной плоскости и имеющие численно равные моменты и одинаковое направление вращения, эквивалентны.

Свойства пар: 1.У пары можно произвольно менять силы и плечо, оставляя при этом неизменным момент пары. 2. Пару можно переносить в плоскости ее действия. 3. Пару можно переносить в плоскость, параллельную плоскости ее действия.

20