теормех / ОТВЕТЫ ТЕОРМЕХ 1
.2.pdfОглавление |
|
1. Введение. Предмет теоретической механики. Механическое движение. Основная задача |
|
теоретической механики. Основные разделы ТМ. ............................................................................ |
5 |
2. Статика. Предмет статики. Основные понятия статики. Аксиомы статики. Основные |
|
задачи статики................................................................................................................................................ |
6 |
3. Система сходящихся сил. Вывод условия равновесия системы сходящихся сил. |
|
Разложение сил. Проекция силы на ось и на плоскость. Примеры. ........................................... |
8 |
4. Теорема о трех силах. Примеры......................................................................................................... |
13 |
5. Связи. Реакции связей. Основные типы реакций связей. Примеры. ................................... |
15 |
6. Система параллельных сил. Сумма параллельных сил. Определение центра тяжести |
|
тел. Момент силы относительно точки. Теорема Вариньона...................................................... |
18 |
7. Пара сил. Вычисление момента пары сил. Теорема об эквивалентности пары сил. |
|
Свойства пары сил...................................................................................................................................... |
20 |
8. Плоская система сил. Теорема о параллельном переносе силы (Основная теорема |
|
статики). Приведение плоской системы сил к единому центру.................................................. |
21 |
1
9. Понятие вектора. Переменные и постоянные векторы. Орты. Разложение вектора по координатным осям. Скалярное и векторное произведение двух векторов. Производная вектора по скалярному аргументу. Направление производной. Свойства производной........ 24
10. Производная от переменного вектора постоянного модуля..................................................... |
31 |
11. Понятие кривизны и радиуса кривизны. Радиус кривизны окружности. .............................. |
34 |
12. Кинематика точки. Закон движения. Основная задача кинематики точки........................... |
35 |
13. Способы задания движения. Векторный, координатный и естественный. Скорости и |
|
ускорения точки при различных способах задания движения. Примеры. .................................. |
36 |
14. Кинематика твердого тела. Поступательное движение твердого тела. Теорема о скоростях |
|
точек поступательно движущегося твердого тела. Вращательное движение твердого тела |
|
вокруг неподвижной оси. Угловая скорость и угловое ускорение. Линейные скорости и |
|
ускорения точек вращающегося твердого тела. Примеры. Со стр 95 ............................................ |
39 |
15. Плоское движение твердого тела. Скорости точек плоской фигуры. Ускорения точек |
|
плоской фигуры............................................................................................................................................. |
44 |
16. Теорема о равенстве проекций скоростей точек плоской фигуры на прямую, |
|
соединяющую эти точки. Мгновенный центр скоростей. Примеры. ............................................. |
49 |
2
17. Динамика точки. Законы Ньютона-Галилея. Дифференциальное уравнение движения |
|
материальной точки. Основные задачи динамики точки. Примеры. ........................................... |
54 |
18. Аналитическое интегрирование дифференциального уравнения прямолинейного |
|
движения точки............................................................................................................................................. |
59 |
19. Количество движения. Импульс силы. Теорема об изменении количества движения |
|
точки. Примеры............................................................................................................................................. |
63 |
20. Кинетический момент (момент количества движения). Теорема об изменении |
|
кинетического момента. ............................................................................................................................. |
66 |
21. Элементарная работа силы. Полная работа силы. Примеры вычисления работы силы |
|
(работа силы тяжести, работа нормальной силы, работа силы упругости, работа силы трения). |
|
Кинетическая энергия. Теорема об изменении кинетической энергии движущейся точки. |
|
Примеры.......................................................................................................................................................... |
68 |
22. Колебательное движение материальной точки. Линейная сила упругости. Коэффициент |
|
жесткости. Статическое отклонение. Свободные прямолинейные колебания материальной |
|
точки. Влияние постоянной силы на свободные колебания. Вынужденные колебания |
|
материальной точки (диф. уравнение и структура его решения). Случай различных частот |
|
собственных колебаний и вынужденных колебаний. Случай равенства частот собственных |
|
колебаний и вынужденных колебаний. Резонанс. ............................................................................. |
82 |
3
23. Понятие механической системы. Масса системы. Внутренние и внешние силы. |
|
Свойства внутренних сил механической системы. Центр масс механической системы. |
|
Момент инерции. Примеры расчета момента инерции для стержня и обруча. Теорема о |
|
движении центра масс системы, следствия из теоремы. Теорема об изменении |
|
кинетического момента механической системы относительно неподвижного центра и |
|
неподвижной оси. Закон сохранения кинетического момента. Дифференциальное |
|
уравнение вращения твердого тела вокруг неподвижной оси. Теорема об изменении |
|
количества движения системы. Закон сохранения количества движения системы. Теорема |
|
об изменении кинетической энергии системы. Случай, когда система является абсолютно |
|
твердым телом.............................................................................................................................................. |
96 |
24. Основы аналитической механики. Малое и действительное бесконечно малое перемещение точки. Возможное перемещение. Элементарная работа силы на возможном перемещении точки. Идеальные связи. Принцип возможных перемещений. Пример. ... 121
4
1. Введение. Предмет теоретической механики. Механическое движение. Основная задача теоретической механики. Основные разделы ТМ.
Теоретическая механика – это наука о механическом движении и механическом взаимодействии материальных тел. Механическим движением называется изменение с течением времени положения материальных тел в пространстве.
Теоретическая механика является базой при изучении механики твердых деформируемых тел, гидромеханики, газовой динамики и многих специальных инженерных дисциплин, таких как: сопротивление материалов, детали машин, теория машин и механизмов, гидравлика, процессы и аппараты химических технологий и др.
Многие явления в химии и в технологических процессах можно описать законами механического движения.
Теоретическая механика состоит из трех частей – статики, кинематики и динамики.
Основная задача теоретической механики. Основной задачей теоретической механики (ТМ) является изучение общих законов движения и взаимодействия материальных тел под действием приложенных к ним сил.
По характеру рассматриваемых задач ТМ принято условно разделять на статику, кинематику и динамику.
Встатике излагается учение о силах и об условиях равновесия тел под действием приложенных сил.
Вкинематике рассматриваются общие геометрические свойства движения тел.
Вдинамике изучаются законы движения материальных тел под действием приложенных сил с учетом массы движущихся тел.
5
2. Статика. Предмет статики. Основные понятия статики. Аксиомы статики. Основные задачи статики.
Статикой называется раздел механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных тел, находящихся под действием сил.
Предмет статики. Статикой называется раздел механики, в котором излагается общее учение о силах, изучаются условия покоя тел, находящихся под действием сил.
Основные понятия статики
Абсолютно твердое тело (АТТ). Тело, в котором расстояние между двумя любыми точками всегда остается постоянным, называется абсолютно твердым. В природе, безусловно, таких тел нет, поскольку при определенных взаимодействиях тела изменяют свою форму. Однако, например, при определении реакций связей данная гипотеза не вносит существенной погрешности.
Материальная точка. Тело, размеры которого по всем направлениям весьма малы, так что различием в движении отдельных точек этого тела можно пренебречь, называется материальной точкой.
Система отсчета. Система координат, неизменно связанная с каким либо физическим телом, относительно которого определяется положение данного движущегося объекта называется система отсчета.
Сила. Величина, являющаяся количественной мерой механического взаимодействия тел, называется силой. За единицу силы в системе СИ принимается Ньютон (Н). Сила, величиной 1 Н, приложенная к покоящемуся телу массой 1 кг, вызывает движение тела с ускорением 1 м/с2. Сила является векторной величиной.
Аксиомы (законы) статики: 1) аксиома инерции: Под действием взаимно уравновешивающихся сил материальная точка (тело) находится в состоянии покоя или движется прямолинейно и равномерно. 2) аксиома равновесия двух сил: Две силы, приложенные к абсолютно твердому телу, будут уравновешены тогда и только тогда, когда они равны по модулю, действуют по одной прямой и направлены в противоположные стороны. 3) аксиома присоединения и исключения уравновешивающихся сил: Действие системы сил на абс. твердое тело не изменится, если к ней прибавить или отнять уравновешенную систему сил. Следствие: Действие силы на абс.тв. тело не изменится, если перенести точку приложения силы вдоль ее линии действия. Т.е. сила, приложенная к абс.тв. телу– скользящий вектор. 4) аксиома параллелограмма сил: Равнодействующая
6
|
|
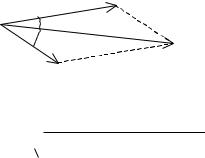
F2 |
|
|
|
|
|
R |
|
|
|
F1 |
двух пересекающихся сил приложена в точке их |
||||
|
|||||
|
|
пересечения и изображается диагональю |
|||
|
|
|
|
|
|
параллелограмма, построенного на этих силах. R |
F1 |
F2 ; |
|||
R
F12 F22 2F1F2 cos . 5) аксиома равенства действия и противодействия (3-
йзакон Ньютона): Всякому действию соответствует равное и противоположно направленное противодействие. 6) принцип отвердевания: Равновесие сил, приложенных к нетвердому телу, не нарушается при его затвердевании
Основными задачами статики являются: - изучение методов преобразования сложных систем сил, приложенных к абсолютно твердому телу, в более простой вид, эквивалентный заданным; - установление условий равновесия тел при действии данной системы сил.
7
3. Система сходящихся сил. Вывод условия равновесия системы сходящихся сил. Разложение сил. Проекция силы на ось и на плоскость. Примеры.
Система сил, линии которых пересекаются в одной точке, называется системой сходящихся сил.
8
Перенося силы вдоль линий их действия можно собрать сходящуюся систему в одной точке — точке пересечения линий действия сил. Далее, находим равнодействующую такой системы сил. Она равна векторной сумме этих сил.
Система сходящихся сил будет уравновешенной (эквивалентной нулю) в том случае, когда ее равнодействующая равна нулю,
т. е. уравнение ∑Fk = 0 является необходимым и достаточным условием k
равновесия системы сходящихся сил.
В плоском случае векторное условие равновесия эквивалентно двум скалярным уравнениям, которые мы получим, взяв проекции векторного равенства на оси, лежащие в плоскости действия сил:
∑FkX = 0, ∑FkY = 0 kk
Втрехмерном случае к этим уравнениям добавится еще одно незави-
симое уравнение ∑FkZ = 0 k
Следует подчеркнуть независимость этого числа (2 — в плоском и 3
9
— в пространственном случаях) уравнений.
Разложение сил - это разложение равнодействующей силы на систему сил. Эта задача является неопределенной и имеет однозначное решение лишь при задании дополнительных условий.
Разложение силы по двум заданным направлениям. Для того чтобы разложить силу 
необходимо знать направление, по которым будет выполнено разложение.
Задача № 2
Нить с двумя телами на концах 
и 
перекинута через блоки 
и 
(рис.2.6). В точке 
к нити, находящейся между блоками, прикрепил груз 
При равновесии системы нить 
образовала
с горизонталью угол 
, а нить 
.
Определить вес тел 
и 
. Силами трения в блоках пренебречь.
Решение. Сначала выясним, равновесие какого объекта надо рассмотреть при решении задачи. По условию задачи нужно определить вес тела 
и
вес тела 
, которые приложены к центрам масс тел и направлены вертикально вниз. Каждое тело натягивает нить с силой, равной его весу. Блок меняет направление нити, а соответственно, и направление силы
натяжения нити. Силы 
и 
по модулю, равны 
и 
, но направлены вдоль 
и 
.
10