3. Рассмотрим теперь частные случаи вращательного движения

а) Равномерное вращение - вращение с постоянной угловой скоростью

( = const):

, , .

Пусть при t = 0: = 0, тогда С = 0 и мы получаем следующее уравнение или закон равномерного вращения:

. (2.33)

в) Равнопеременное вращение - это вращение с постоянным угловым ускорением ( = const):

, , ,

, ,

.

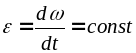Пусть при t = 0: _ и _ = 0, тогда С₁ = _ , C₂ = 0. Подставляя найденные значения констант интегрирования в полученные выше выражения, получаем:

, (2.34)

. (2.35)

В полученном законе изменения угловой скорости (2.34) и в уравнении равнопеременного вращения (2.35), угловое ускорение  будет положительным при равноускоренном вращении и отрицательным при равнозамедленным.

В заключение приведем вполне очевидные соотношения, которые часто используются при решении задач:

, (2.36)

где N - число оборотов, n - угловая скорость в оборотах в минуту.

4. Формула Эйлера

В заключение получим векторные формулы для скорости и ускорения точек в круговом движении. Рассмотри движение точки М, не лежащей на оси вращения (рис. 2.22). Покажем, что ее скорость полностью определяется формулой Эйлера : . (2.37)

Рис. 2.22. Иллюстрация формулы Эйлера

Действительно, модуль векторного произведения равен V=r sin = R, что совпадает с выражением (2.29). Формула (2.34) правильно определяет и направление вектора скорости: вектор направлен перпендикулярно плоскости треугольника ОСМ в ту сторону, откуда поворот от к виден происходящим против хода часовой стрелки (т.е. вектор направлен, как и полагается, по касательной к траектории в направлении вращения тела).

Для вывода векторных формул, определяющих ускорение, продифференцируем формулу Эйлера по времени:

.

Учитывая, что согласно (2.28) и (2.5)

,

получаем:

, (2.38)

где , . (2.39)

В справедливости выражений (2.36) можно убедиться непосредственно, определив модули и направления входящих в них векторных произведений. Так согласно первой формуле (2.39) , что совпадает с уже известным выражением (2.30). Правильно определяется и направление вектора (см. рис.2.22). Вторая формула (2.39) дает [сравните с (2.31)]. Направлен вектор , как и положено, перпендикулярно плоскости, в которой лежат перемножаемы векторы внутрь траектории, откуда поворот от к вектору виден происходящим против хода часовой стрелки.

Лекция 14

Вопросы