
теормех / шпоры термех 1 курс
.doc1
Кинематика – раздел механики, в котором изучаются движение материальных тел с геометрической точки зрения, без учета массы и действующих на них сил. Способы задания движения точки: 1) естественный, 2) координатный, 3) векторный. Траектория точки – непрерывная кривая, которую описывает точка при своем движении. Естественный сп. указывается траектория точки, закон ее движения по этой траектории, начало и направление отсчета дуговой координаты: s=f(t) – закон движения точки. При прямолинейном движении: х=f(t). Координатный сп. положение точки в пространстве определяется тремя координатами, изменения которых определяют закон движения точки: x=f1(t), y=f2(t), z=f3(t).
Е
 сли
движение в плоскости, то два уравнения
движения. Уравнения движения описывают
уравнение траектории в параметрической
форме. Исключив из уравнений параметр
t,
получаем уравнение траектории в обычном
виде: f(x,y)=0
(для плоск-ти). Векторный
сп.
положение точки определяется ее
радиус-вектором
сли
движение в плоскости, то два уравнения
движения. Уравнения движения описывают
уравнение траектории в параметрической
форме. Исключив из уравнений параметр
t,
получаем уравнение траектории в обычном
виде: f(x,y)=0
(для плоск-ти). Векторный
сп.
положение точки определяется ее
радиус-вектором
![]() ,
проведенным из какого-либо центра. Связь
между координатным и векторным способами:
,
проведенным из какого-либо центра. Связь
между координатным и векторным способами:
![]() ,
модуль
,
модуль
![]() .
.
Скорость
точки.
Вектор ск-сти:
![]() – первая производная от радиус-вектора
по времени ;
– первая производная от радиус-вектора
по времени ;
![]() .
Проекции скорости:
.
Проекции скорости:
![]() ,
,![]() ,
,
![]() .
Модуль скорости:
.
Модуль скорости:
![]() ,
направляющие косинусы:
,
направляющие косинусы:
![]() и т.д. Если модуль скорости не изменяется
с течением времени, то движение называется
равномерным. При естественном сп.:
и т.д. Если модуль скорости не изменяется
с течением времени, то движение называется
равномерным. При естественном сп.:
![]() – модуль скорости, вектор скорости:
– модуль скорости, вектор скорости:
![]() ,
,
![]() –
орт касательной, т.е. скорость
всегда направлена по касательной к
траектории.
Если v>0,
то движение происходит в сторону
положительного отсчета дуговой координаты
и наоборот. Движение в полярной системе
координат: r=r(t)
– полярный радиус, =(t)
–
орт касательной, т.е. скорость
всегда направлена по касательной к
траектории.
Если v>0,
то движение происходит в сторону
положительного отсчета дуговой координаты
и наоборот. Движение в полярной системе
координат: r=r(t)
– полярный радиус, =(t)
2
У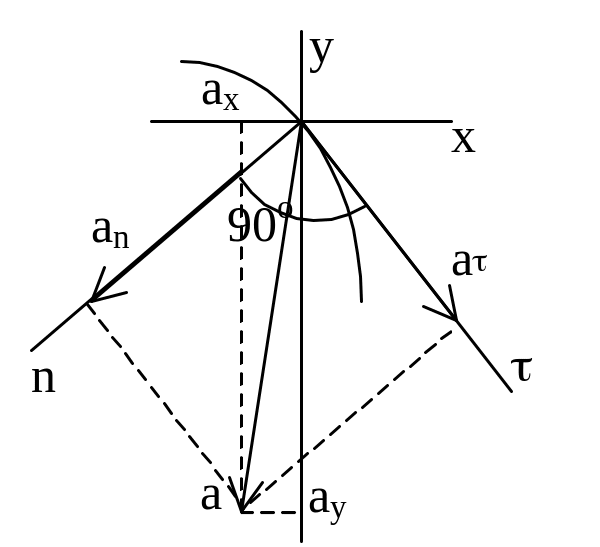
 скорение
точки.
скорение
точки.
![]() ,
[м/сек2].
Проекции уск.-я:
,
[м/сек2].
Проекции уск.-я:
![]() и т.д. Модуль уск.-я:
и т.д. Модуль уск.-я:![]() .
При естественным сп. задания движения
полное ускорение раскладывают на
нормальное и касательное (тангенциальное)
ускорения:
.
При естественным сп. задания движения
полное ускорение раскладывают на
нормальное и касательное (тангенциальное)
ускорения:
![]() .
Модуль нормального ускорения:
.
Модуль нормального ускорения:
![]() ,
– радиус кривизны траектории, нормальное
ускорение направлено по нормали к
траектории (
к касательной) всегда
к центру кривизны, т.е. в сторону
вогнутости. Нормальное ускорение
характеризует изменение скорости по
направлению. Модуль касательного
ускорения
,
– радиус кривизны траектории, нормальное
ускорение направлено по нормали к
траектории (
к касательной) всегда
к центру кривизны, т.е. в сторону
вогнутости. Нормальное ускорение
характеризует изменение скорости по
направлению. Модуль касательного
ускорения
![]() ,
направлено по касательной к траектории,
либо в сторону скорости, либо в обратную.
Касательное ускорение характеризует
изменение скорости по величине. При
ускоренном движ-ии направление касат.
уск. и скорости совпадают, при замедленном
– противоположно.
,
направлено по касательной к траектории,
либо в сторону скорости, либо в обратную.
Касательное ускорение характеризует
изменение скорости по величине. При
ускоренном движ-ии направление касат.
уск. и скорости совпадают, при замедленном
– противоположно.
![]()
![]() ,
,
![]() ..
..
3
П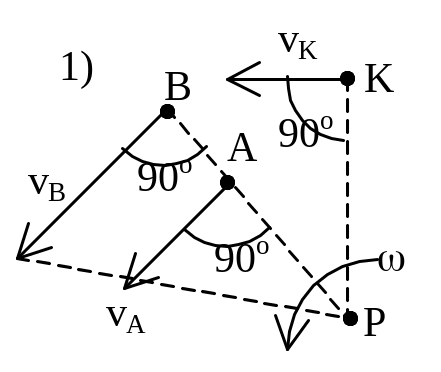 ростейшие
движения твердого тела: поступательное
и вращение вокруг неподвижной оси.
Поступательное
движение
тела – такое движение твердого тела,
при котором любая прямая, проведенная
в этом теле, перемещается, оставаясь
параллельное самой себе. При поступат.
движ. все точки тела описывают одинаковые
траектории и имеют в каждый момент
времени одинаковые по модулю и направлению
скорости и ускорения. Вращательное
движение
тела – такое движение твердого тела,
при котором все точки, принадлежащие
некоторой прямой, неизменно связанной
с телом, остаются неподвижными. Эта
прямая называется осью вращения тела.
При этом движении все точки тела движутся
в плоскостях, перпендикулярных оси
вращения, и описывают окружности, центры
которых лежат на оси вращения. Урав-ние
(закон) вращательного движ.: =f(t)
– угол поворота тела в радианах.
ростейшие
движения твердого тела: поступательное
и вращение вокруг неподвижной оси.
Поступательное
движение
тела – такое движение твердого тела,
при котором любая прямая, проведенная
в этом теле, перемещается, оставаясь
параллельное самой себе. При поступат.
движ. все точки тела описывают одинаковые
траектории и имеют в каждый момент
времени одинаковые по модулю и направлению
скорости и ускорения. Вращательное
движение
тела – такое движение твердого тела,
при котором все точки, принадлежащие
некоторой прямой, неизменно связанной
с телом, остаются неподвижными. Эта
прямая называется осью вращения тела.
При этом движении все точки тела движутся
в плоскостях, перпендикулярных оси
вращения, и описывают окружности, центры
которых лежат на оси вращения. Урав-ние
(закон) вращательного движ.: =f(t)
– угол поворота тела в радианах.
Угловая
ск-сть:
![]() ,
[рад/с] – определяет быстроту изменения
угла поворота.
,
[рад/с] – определяет быстроту изменения
угла поворота.
В ектор
угловой скорости тела, совершающего
вращение вокруг неподвижной оси,
направлен вдоль оси вращения так, что
если смотреть ему навстречу вращение
будет против час. стрелки. Угловое
ускорение тела:
ектор
угловой скорости тела, совершающего
вращение вокруг неподвижной оси,
направлен вдоль оси вращения так, что
если смотреть ему навстречу вращение
будет против час. стрелки. Угловое
ускорение тела:
![]() ,
[рад/с2].
Вектор углового ускорения также направлен
вдоль оси вращения. При ускоренном
движении совпадает по направлению с
угловой скоростью и противоположно при
замедленном вращении.
,
[рад/с2].
Вектор углового ускорения также направлен
вдоль оси вращения. При ускоренном
движении совпадает по направлению с
угловой скоростью и противоположно при
замедленном вращении.
Равнопеременное
вращение: =0+t;
![]() ,
здесь начальный угол 0=0.
,
здесь начальный угол 0=0.
Скорости
и ускорения точек вращающегося тела.
![]() – скорость любой точки твердого тела,
вращающегося вокруг неподвижной оси,
равна векторному произведению вектора
угловой скорости тела на радиус–вектор
этой точки. Модуль векторного произведения:
v=rsin().
Направлен вектор скорости по касательной
к окружности, по которой перемещается
точка М, в сторону вращения.
– скорость любой точки твердого тела,
вращающегося вокруг неподвижной оси,
равна векторному произведению вектора
угловой скорости тела на радиус–вектор
этой точки. Модуль векторного произведения:
v=rsin().
Направлен вектор скорости по касательной
к окружности, по которой перемещается
точка М, в сторону вращения.
Вращательное
ускорение
![]() ,
модуль вращат. уск. авр=rsin,
направлено по касательной к траектории
точки, т.е. параллельно скорости.
Центростремительное (осестремительное)
ускорение
,
модуль вращат. уск. авр=rsin,
направлено по касательной к траектории
точки, т.е. параллельно скорости.
Центростремительное (осестремительное)
ускорение
![]() ,
ац=2R,
направлено по радиусу к оси (центру)
вращения. Модуль полного уск.:
,
ац=2R,
направлено по радиусу к оси (центру)
вращения. Модуль полного уск.:
![]() .
.
4
Плоское движение твердого тела.
П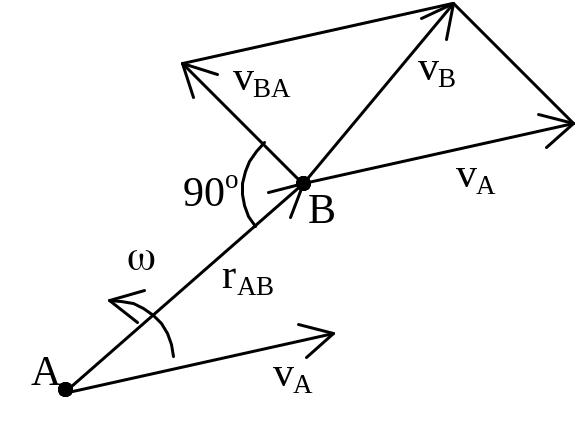
 лоским
(плоскопараллельным) назыв. такое
движение, при котором все его точки
перемещаются параллельно некоторой
неподвижной плоскости. Уравнения
плоского движения:
xA=
f1(t),
yA=
f2(t),
= f3(t),
точка А назыв. полюсом. Плоское движение
тв.тела слагается из поступательного
движения, при котором все точки тела
движутся так же, как полюс (А),и из
вращательного движения вокруг этого
полюса. Поступательное перемещение
зависит от выбора полюса, а величина и
направление угла поворота не зависят.
Скорости
точек тела при плоском движении:
лоским
(плоскопараллельным) назыв. такое
движение, при котором все его точки
перемещаются параллельно некоторой
неподвижной плоскости. Уравнения
плоского движения:
xA=
f1(t),
yA=
f2(t),
= f3(t),
точка А назыв. полюсом. Плоское движение
тв.тела слагается из поступательного
движения, при котором все точки тела
движутся так же, как полюс (А),и из
вращательного движения вокруг этого
полюса. Поступательное перемещение
зависит от выбора полюса, а величина и
направление угла поворота не зависят.
Скорости
точек тела при плоском движении:
![]() ;
;
![]() ,
vBA=
BA,
т.е. скорость какой-либо точки В плоской
фигуры равна геометрической сумме
скорости полюса А и скорости точки В
при вращении плоской фигуры вокруг
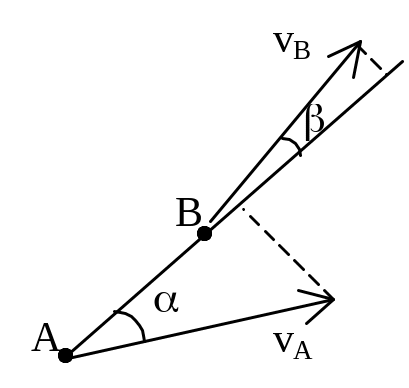
полюса А. Теорема: при плоском движении
проекции скоростей двух точек тела на
ось, проходящую через эти точки, равны
между собой: vAcos
= vBcos.
Мгновенный
центр скоростей
– точка плоской фигуры, скорость которой
в данный момент равна нулю – Р. Если
тело движется непоступательно, т.е. 0,
то мгн.цент.ск. всегда существует.
,
vBA=
BA,
т.е. скорость какой-либо точки В плоской
фигуры равна геометрической сумме
скорости полюса А и скорости точки В
при вращении плоской фигуры вокруг
полюса А. Теорема: при плоском движении
проекции скоростей двух точек тела на
ось, проходящую через эти точки, равны
между собой: vAcos
= vBcos.
Мгновенный
центр скоростей
– точка плоской фигуры, скорость которой
в данный момент равна нулю – Р. Если
тело движется непоступательно, т.е. 0,
то мгн.цент.ск. всегда существует.
![]() – скорость любой точки плоской фигуры
имеет модуль, равный произведению
угловой скорости фигуры на длину отрезка,
соединяющего точку с м.ц.с., и направлена
этому отрезку в сторону вращения фигуры.
– скорость любой точки плоской фигуры
имеет модуль, равный произведению
угловой скорости фигуры на длину отрезка,
соединяющего точку с м.ц.с., и направлена
этому отрезку в сторону вращения фигуры.
![]() ,
скорости точек тела пропорциональны
их расстояниям до м.ц.с.
,
скорости точек тела пропорциональны
их расстояниям до м.ц.с.
![]() ,
угловая скорость тела равна отношению
скорости какой-нибудь точки к ее
расстоянию до м.ц.с. Определение положения
м.ц.с.: 1) м.ц.с. – точка пересечения
перпендикуляров, восстановленных к
скоростям точек (напр. в точке В и точке
К); 2) если скорости точек А и В параллельны
между собой и перпендикулярны АВ, то
для определения м.ц.с. должны быть
известны модули и направления скоростей
(см. vA
и vB);
3) если они при этом равны между собой,
то м.ц.с. находится в ,
а угловая скорость =vA/=0;
4) если известно, что скорости двух точек
А и В равны, параллельны и не
перпендикулярны АВ, то м.ц.с. в ,
и угловая скорость =vA/=0,
если это имеет место только к некоторый
момент времени, то имеем мгновенное
поступательное движение; 5) если плоская
фигура катится без скольжения по
неподвижной поверхности, то м.ц.с. плоской
фигуры будет в точке соприкасания.
,
угловая скорость тела равна отношению
скорости какой-нибудь точки к ее
расстоянию до м.ц.с. Определение положения
м.ц.с.: 1) м.ц.с. – точка пересечения
перпендикуляров, восстановленных к
скоростям точек (напр. в точке В и точке
К); 2) если скорости точек А и В параллельны
между собой и перпендикулярны АВ, то
для определения м.ц.с. должны быть
известны модули и направления скоростей
(см. vA
и vB);
3) если они при этом равны между собой,
то м.ц.с. находится в ,
а угловая скорость =vA/=0;
4) если известно, что скорости двух точек
А и В равны, параллельны и не
перпендикулярны АВ, то м.ц.с. в ,
и угловая скорость =vA/=0,
если это имеет место только к некоторый
момент времени, то имеем мгновенное
поступательное движение; 5) если плоская
фигура катится без скольжения по
неподвижной поверхности, то м.ц.с. плоской
фигуры будет в точке соприкасания.
5
Ускорения
точек:
![]() ,
,
![]()
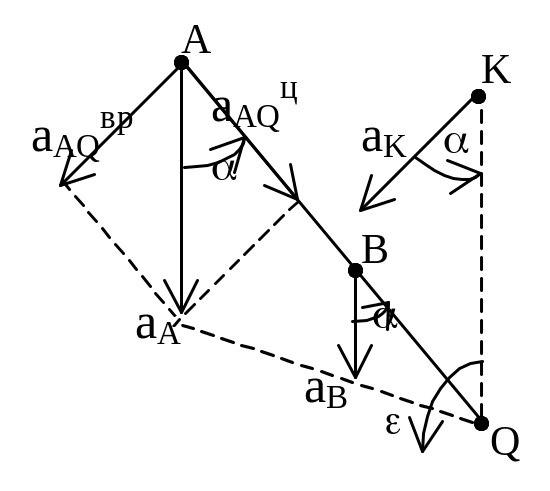 –
ускорение
любой точки (В) фигуры геометрически
складывается из ускорения полюса (А) и
центростремительного и вращательного
ускорений во вращательном движении
тела относительно полюса.
–
ускорение
любой точки (В) фигуры геометрически
складывается из ускорения полюса (А) и
центростремительного и вращательного
ускорений во вращательном движении
тела относительно полюса.
![]() ,
,
![]() ,
,
,
,
![]() .
Мгновенный
центр ускорений
– точка (Q)
плоской фигуры, ускорение которой в
данный момент времени равно нулю. Для
его построения из точки А откладываем
под углом
.
Мгновенный
центр ускорений
– точка (Q)
плоской фигуры, ускорение которой в
данный момент времени равно нулю. Для
его построения из точки А откладываем
под углом
![]() к ускорению аА
отрезок
к ускорению аА
отрезок
![]() ,
при этом угол откладывается от ускорения
в сторону, направления углового ускорения
.
Модули ускорений точек плоской фигуры
пропорциональны расстояниям от этих
точек до мгн.ц. ускорений, а векторы
ускорений составляют с отрезками,
соединяющими эти точки и м.ц.у. один и
тот же угол
:
,
при этом угол откладывается от ускорения
в сторону, направления углового ускорения
.
Модули ускорений точек плоской фигуры
пропорциональны расстояниям от этих
точек до мгн.ц. ускорений, а векторы
ускорений составляют с отрезками,
соединяющими эти точки и м.ц.у. один и
тот же угол
:
![]() .
Мгновенный центр скоростей Р и мгновенный
центр ускорений Q
являются различными точками плоской
фигуры.
.
Мгновенный центр скоростей Р и мгновенный
центр ускорений Q
являются различными точками плоской
фигуры.
6
Сложное
движение точки (тела)
– такое движение, при котором точка
(тело) одновременно участвует в нескольких
движениях (напр. пассажир, перемещающийся
по движущемуся вагону). В этом случае
вводится подвижная система координат
(Oxyz),
которая совершает заданное движение
относительно неподвижной (основной)
системы координат (O1x1y1z1).
Абсолютным
движением
точки назыв. движение по отношению к
неподвижной системе координат.
Относительное
движение
– движение по отношению к подвижной
системе коорд. (движение по вагону).
Переносное
движение
– движение подвижной сист. координат
относительно неподвижной (движение
вагона). Теорема
о сложении скоростей:
![]() ,
,
![]() ;
;
![]() -орты
(единичные вектора) подвижной системы
координат, орт вращается вокруг мгновенной
оси, поэтому скорость его конца
-орты
(единичные вектора) подвижной системы
координат, орт вращается вокруг мгновенной
оси, поэтому скорость его конца
![]() и т.д., :
и т.д., :
![]() ,
,
![]() ;
;
![]() –
относительная скорость.
–
относительная скорость.
![]() ;
переносная скорость:
;
переносная скорость:
![]() ,
поэтому абсолютная скорость точки =
геометрической сумме ее переносной
(ve)
и относительной (vr)
скоростей
,
поэтому абсолютная скорость точки =
геометрической сумме ее переносной
(ve)
и относительной (vr)
скоростей
![]() ,
модуль:
,
модуль:
![]() .
Теорема
о сложении ускорений (теорема Кориолиса):
.
Теорема
о сложении ускорений (теорема Кориолиса):

![]()
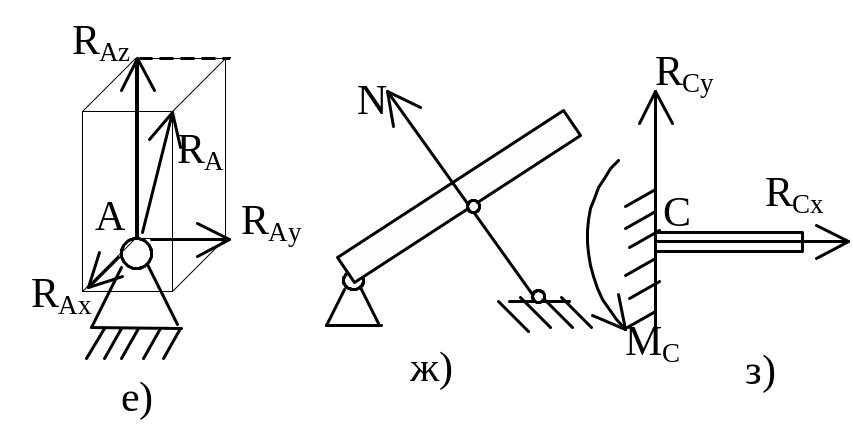 и
т.д. Слагаемые выражения, определяющего
ускорения
и
т.д. Слагаемые выражения, определяющего
ускорения
![]() :
1)
:
1)
![]() –
ускорение полюса О;
–
ускорение полюса О;
2)
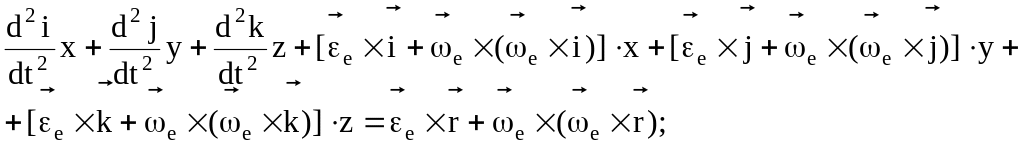
3)
![]() –
относительное ускорение точки;
–
относительное ускорение точки;
4)
![]() ,
,
получаем:
![]() .
.
П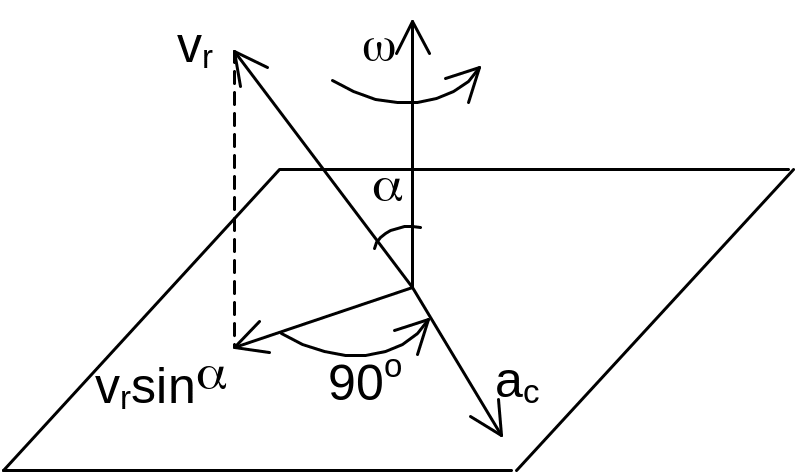
 ервые
три слагаемых представляют собой
ускорение точки в переносном движении:
ервые
три слагаемых представляют собой
ускорение точки в переносном движении:
![]() –
ускорение полюса О;
–
ускорение полюса О;
![]() – вращательное уск.,
– вращательное уск.,
![]() – осестремительное уск., т.е.
– осестремительное уск., т.е.
![]() .
Теорема
о сложении ускорений (теорема Кориолиса):
.
Теорема
о сложении ускорений (теорема Кориолиса):
![]() ,
где
,
где
![]() – ускорение Кориолиса (кориолисово
ускорение) – в случае непоступательного
переносного движения абсолютное
ускорение = геометрической сумме
переносного, относительного и кориолисова
ускорений. Кориолисово ускорение
характеризует: 1) изменение модуля и
направления переносной скорости точки
из-за ее относительного движения; 2)
изменение направления относительной
скорости точки из-за вращательного
переносного движения. Модуль ускорения
Кориолиса: ас=
2|evr|sin(e^vr),
направление вектора
– ускорение Кориолиса (кориолисово
ускорение) – в случае непоступательного
переносного движения абсолютное
ускорение = геометрической сумме
переносного, относительного и кориолисова
ускорений. Кориолисово ускорение
характеризует: 1) изменение модуля и
направления переносной скорости точки
из-за ее относительного движения; 2)
изменение направления относительной
скорости точки из-за вращательного
переносного движения. Модуль ускорения
Кориолиса: ас=
2|evr|sin(e^vr),
направление вектора
![]() определяется
по правилу векторного произведения,
или по правилу Жуковского: проекцию
относительной скорости на плоскость,
перпендикулярную переносной угловой
скорости, надо повернуть на 90о
в направлении вращения.
определяется
по правилу векторного произведения,
или по правилу Жуковского: проекцию
относительной скорости на плоскость,
перпендикулярную переносной угловой
скорости, надо повернуть на 90о
в направлении вращения.
Кориолисово уск. = 0 в трех случаях: 1) e=0, т.е. в случае поступательного переносного движения или в момент обращения угл. скорости в 0; 2) vr=0; 3) sin(e^vr)=0, т.е. (e^vr)=0, когда относительная скорость vr параллельна оси переносного вращения. В случае движения в одной плоскости – угол между vr и вектором e = 90о, sin90o=1, ас=2evr.
7
Статика – раздел теор.мех., в котором рассмат-ся задачи на равновесие систем сил.
Сила
–
мера механического взаимодействия тел.
Сила векторная величина, характеризуется
тремя элементами: числовым значением
(модулем), направлением и точкой
приложения. Ед.измерения – ньютон,
![]() ,
1кН (килоньютон)= 103Н.
,
1кН (килоньютон)= 103Н.
Прямая, по которой направлена сила, назыв. линией действия силы.
Аксиомы
(законы) статики:
1) аксиома инерции: Под действием взаимно
уравновешивающихся сил материальная
точка (тело) находится в состоянии покоя
или движется прямолинейно и равномерно.
2) аксиома равновесия двух сил: Две силы,
приложенные к абсолютно твердому телу,
будут уравновешены тогда и только тогда,
когда они равны по модулю, действуют по
одной прямой и направлены в противоположные
стороны. 3) аксиома присоединения и
исключения уравновешивающихся сил:
Действие системы сил на абс. твердое
тело не изменится, если к ней прибавить
или отнять уравновешенную систему сил.
Следствие: Действие силы на абс.тв. тело
не изменится, если перенести точку
приложения силы вдоль ее линии действия.
Т.е. сила, приложенная к абс.тв. телу–
скользящий вектор. 4) аксиома параллелограмма
сил: Равнодействующая двух пересекающихся
сил приложена в точке их пересечения и
изображается диагональю параллелограмма,
построенного на этих силах.
![]() ;
;
![]()
 .
5) аксиома равенства действия и
противодействия (3-й закон Ньютона):
Всякому действию соответствует равное
и противоположно направленное
противодействие. 6) принцип отвердевания:
Равновесие сил, приложенных к нетвердому
телу, не нарушается при его затвердевании.
.
5) аксиома равенства действия и
противодействия (3-й закон Ньютона):
Всякому действию соответствует равное
и противоположно направленное
противодействие. 6) принцип отвердевания:
Равновесие сил, приложенных к нетвердому
телу, не нарушается при его затвердевании.
Т ело
называется свободным,
если его перемещения ничем не ограничены.
Тело, перемещение которого ограничено
другими телами, назыв. несвободным.
Тела, ограничивающие перемещения данного
тела, назыв. связями.
Силы, с которыми связи действуют на
данное тело, назыв. реакциями
связей.
Принцип
освобождаемости:
Всякое несвободное тело можно рассматривать
как свободное, если действие связей
заменить их реакциями, приложенными к
телу. Основные
типы связей:
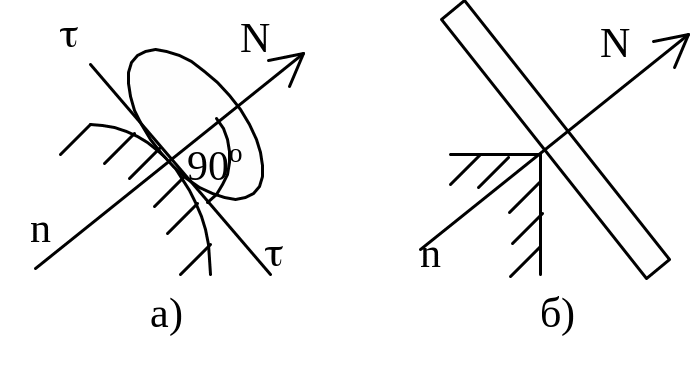
а) опора на идеально гладкую поверхность
– реакция поверхности направлена по
нормали к ней, т.е. перпендикулярно
касательной – нормальная реакция; б)
одна из соприкасающихся поверхностей
является точкой (угол), реакция направлена
по нормали к другой поверхности; в) нить
– реакция направлена вдоль нити к точке
подвеса; г) цилиндрический шарнир
(шарнирно-неподвижная опора) – реакция
может иметь любое направление в плоскости.
При решении задач заменяется двумя
взаимно перпендикулярными составляющими;
д) цилиндрическая шарнирно-подвижная
опора (шарнир на катках) – реакция
направлена перпендикулярно опорной
плоскости; е) сферический (шаровой)
шарнир – реакция может иметь любое
направление в пространстве. При решении
задач заменяется тремя взаимно
перпендикулярными составляющими; ж)
невесомый стержень (обязательно
невесомый) – реакция направлена вдоль
стержня; з) "глухая" заделка
(вмурованная балка) – возникает
произвольно направленная реакция –
сила и реактивный момент, также неизвестный
по направлению. Реакция раскладывается
на две составляющие.
ело
называется свободным,
если его перемещения ничем не ограничены.
Тело, перемещение которого ограничено
другими телами, назыв. несвободным.
Тела, ограничивающие перемещения данного
тела, назыв. связями.
Силы, с которыми связи действуют на
данное тело, назыв. реакциями
связей.
Принцип
освобождаемости:
Всякое несвободное тело можно рассматривать
как свободное, если действие связей
заменить их реакциями, приложенными к
телу. Основные
типы связей:
а) опора на идеально гладкую поверхность
– реакция поверхности направлена по
нормали к ней, т.е. перпендикулярно
касательной – нормальная реакция; б)
одна из соприкасающихся поверхностей
является точкой (угол), реакция направлена
по нормали к другой поверхности; в) нить
– реакция направлена вдоль нити к точке
подвеса; г) цилиндрический шарнир
(шарнирно-неподвижная опора) – реакция
может иметь любое направление в плоскости.
При решении задач заменяется двумя
взаимно перпендикулярными составляющими;
д) цилиндрическая шарнирно-подвижная
опора (шарнир на катках) – реакция
направлена перпендикулярно опорной
плоскости; е) сферический (шаровой)
шарнир – реакция может иметь любое
направление в пространстве. При решении
задач заменяется тремя взаимно
перпендикулярными составляющими; ж)
невесомый стержень (обязательно
невесомый) – реакция направлена вдоль
стержня; з) "глухая" заделка
(вмурованная балка) – возникает
произвольно направленная реакция –
сила и реактивный момент, также неизвестный
по направлению. Реакция раскладывается
на две составляющие.
С

 истема
сходящихся сил.
Сходящимися называются силы, линии
действия которых пересекаются в одной
точке. Равнодействующая
сходящихся сил
равна геометрической сумме этих сил и
приложена в точке их пересечения
истема
сходящихся сил.
Сходящимися называются силы, линии
действия которых пересекаются в одной
точке. Равнодействующая
сходящихся сил
равна геометрической сумме этих сил и
приложена в точке их пересечения
![]() .
Равнодействующая может быть найдена
геометрич. способом – построением
силового (векторного) многоугольника
или аналитич. способом, проектируя силы
на оси координат. Проекции
силы на оси координат
(для плоской сист.): Fx=Fcos;
Fy=Fcos=Fsin;
проекция >0, если направление составляющей
силы совпадает с направл. оси. Модуль
силы:
.
Равнодействующая может быть найдена
геометрич. способом – построением
силового (векторного) многоугольника
или аналитич. способом, проектируя силы
на оси координат. Проекции
силы на оси координат
(для плоской сист.): Fx=Fcos;
Fy=Fcos=Fsin;
проекция >0, если направление составляющей
силы совпадает с направл. оси. Модуль
силы:![]()
![]() ;
направляющие
косинусы:
;
направляющие
косинусы:
![]() разложение силы на составляющие:
разложение силы на составляющие:
![]() ,
где
,
где
![]() – орт
(единичный вектор) соответствующей оси.
– орт
(единичный вектор) соответствующей оси.
Д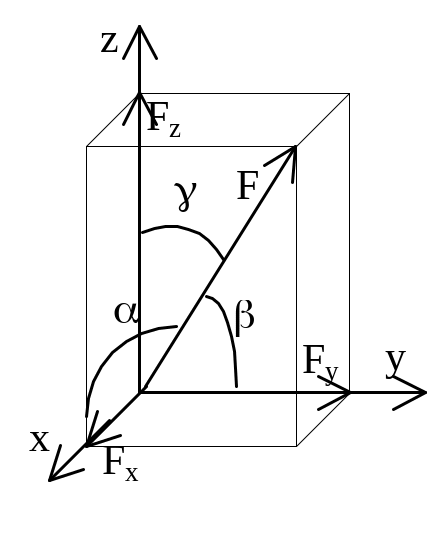 ля
пространственной системы:
ля
пространственной системы:
![]() ,
,
Fx=Fcos;
Fy=Fcos;
Fz=Fcos;
![]() ;
;
![]() .
.
Проекции
равнодействующей системы сходящихся
сил на координатные оси равна алгебраическим
суммам проекций этих сил на соответствующие
оси: Rx=Fix;
Ry=Fiy;
Rz=Fiz;
![]() .
.
8![]()
Условия
равновесия сист. сходящихся сил:
геометрическое:![]()
аналитические: Fix=0; Fiy=0; Fiz=0. Теорема о трех непараллельных силах: Если под действием трех сил тело находится в равновесии и линии действия двух сил пересекаются, то все силы лежат в одной плоскости и их линии действия пересекаются в одной точке.
Теория пар сил. Сложение двух параллельных сил: равнодейст-ющая двух парал-ых сил F1 и F2 одного направления имеет такое же направление, ее модуль равен сумме модулей слагаемых сил, а точка приложения делит отрезок между точками приложения сил на части обратно пропорциональные модулям сил: R=F1 + F2; АС/ВС=F2/F1. Равнодействующая двух противоположно направленных паралл-ных сил имеет направление силы большей по модулю и модуль, равный разности модулей сил.
Система двух параллельных сил, равных по модулю и направленных в разные стороны, назыв. парой сил. Кратчайшее расстояние между линиями действия этих сил назыв. плечом пары "h". Действия пары сил характеризуется ее моментом. Момент пары сил M = Fh – произведение модуля одной из сил пары на ее плечо.
Момент
пары сил
![]() – вектор, направленный перпендикулярно
плоскости сил, так, что, если смотреть
ему навстречу, то видим вращение пары
против хода час.стр. M>0,
если против час.стр., M<0
– по час.стр (на рис М>0).
– вектор, направленный перпендикулярно
плоскости сил, так, что, если смотреть
ему навстречу, то видим вращение пары
против хода час.стр. M>0,
если против час.стр., M<0
– по час.стр (на рис М>0).
Теоремы
о парах.
1) Две пары, лежащие в одной плоскости,
можно заменить одной парой, лежащей в
той же плоскости, с моментом, равным
сумме моментов данных двух пар.
![]() .
2) Две пары, имеющие геометрически равные
моменты, эквиваленты. 3) Не нарушая
состояния твердого тела, пару сил можно
переносить в плоскости ее действия.
Т.е. момент пары сил является свободным
вектором. 4) Система нескольких пар сил
эквивалента одной паре, момент которой
равен векторной сумме моментов данных
пар. Т.е. система пар приводится к одной
паре, момент которой равен сумме моментов
всех пар. Условие равновесия пар сил:
.
2) Две пары, имеющие геометрически равные
моменты, эквиваленты. 3) Не нарушая
состояния твердого тела, пару сил можно
переносить в плоскости ее действия.
Т.е. момент пары сил является свободным
вектором. 4) Система нескольких пар сил
эквивалента одной паре, момент которой
равен векторной сумме моментов данных
пар. Т.е. система пар приводится к одной
паре, момент которой равен сумме моментов
всех пар. Условие равновесия пар сил:
![]() – геометрическая сумма их моментов
равна 0. Пары сил, расположенные в одной
плоскости, взаимно уравновеш-тся, если
алгебраическая сумма их моментов Мi=0.
– геометрическая сумма их моментов
равна 0. Пары сил, расположенные в одной
плоскости, взаимно уравновеш-тся, если
алгебраическая сумма их моментов Мi=0.
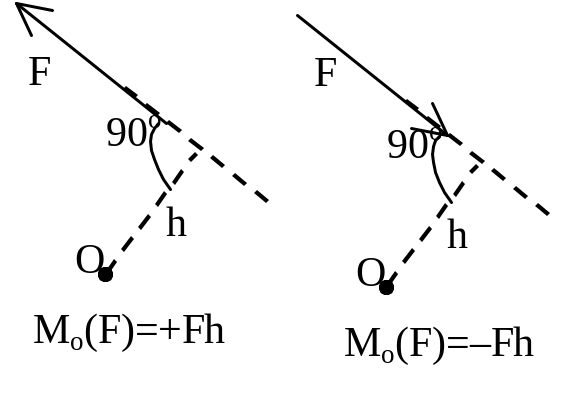
Момент
силы относительно точки
– вектор, численно равный произведению
модуля силы на плечо и направленный
перпендикулярно плоскости, содержащей
силу и точку, в такую сторону, чтобы
смотря ему навстречу, видеть силу
стремящейся повернуться против хода
час.стрелки. Плечо "h"–
кратчайшее расстояние от точки до линии
действия силы.
![]() – момент силы равен векторному
произведению вектора
– момент силы равен векторному
произведению вектора
![]() на вектор
на вектор
![]() .
Модуль векторного произведения:
.
Модуль векторного произведения:
![]() RFsin=
Fh.
Для плоской сист. сил обычно находят не
вектор момента, а только его модуль:
Fh,
>0 – против час.стр.; <0 – по час.стр.
Свойства момента силы: 1) момент силы не
изменяется при переносе точки приложения
силы вдоль ее линии действия; 2) момент
силы относит. точки =0 только тогда, когда
сила =0 или когда линия действия силы
проходит через точку (т.е. плечо =0). Если
x,y,z
– координаты точки приложения силы,
Fx,
Fy,
Fz
– проекции силы на оси координат и точка
0 – начало координат, то
RFsin=
Fh.
Для плоской сист. сил обычно находят не
вектор момента, а только его модуль:
Fh,
>0 – против час.стр.; <0 – по час.стр.
Свойства момента силы: 1) момент силы не
изменяется при переносе точки приложения
силы вдоль ее линии действия; 2) момент
силы относит. точки =0 только тогда, когда
сила =0 или когда линия действия силы
проходит через точку (т.е. плечо =0). Если
x,y,z
– координаты точки приложения силы,
Fx,
Fy,
Fz
– проекции силы на оси координат и точка
0 – начало координат, то
![]()
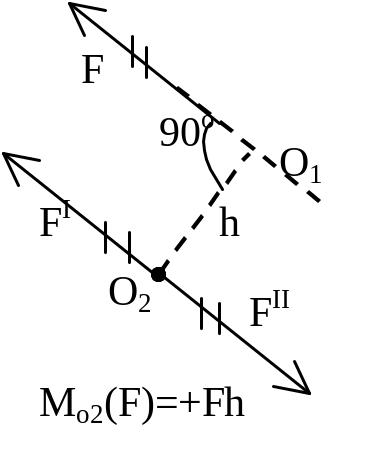 =(yFz
– zFy)
=(yFz
– zFy)![]() +(zFx
– xFz)
+(zFx
– xFz)![]() +(xFy
– yFx)
+(xFy
– yFx)![]() ,
откуда проекции момента силы на оси
коорд.: М0x(
)=yFz
– zFy;
М0y(
)=zFx
– xFz;
М0z(
)=xFy
– yFx.
,
откуда проекции момента силы на оси
коорд.: М0x(
)=yFz
– zFy;
М0y(
)=zFx
– xFz;
М0z(
)=xFy
– yFx.
