ответы / 8

8. ИЗГИБ

Плоский изгиб балок

Изгибом называется вид нагружения стержня, при котором в его поперечном сечении возникает изгибающий момент. Стержень, при изгибе, называется балкой.

Изгиб называется плоским, если Мх  0 и Qy  0 , а М y  Qх  N  T  0 .

Чистый изгиб

Если в поперечных сечениях возникает только изгибающий момент М х , то изгиб называется чистым.

Нормальные напряжения при чистом изгибе

 при изгибе продольные слои балки не взаимодействуют друг с другом в перпендикулярных к ним направлениях, Из этого предположения следует, что в любой точке балки х  у  0 ;

 поперечные сечения балки, плоские до деформации, после деформации остаются плоскими и перпендикулярными к продольной оси (гипотеза плоских сечений);

 напряжения в поперечных сечениях балки не изменяются по его ширине.

Кроме того, полагается, что связь между напряжением и деформацией определяется законом Гука   Е ,

формулу для определения нормальных напряжений в сечениях стержня при чистом изгибе:

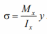
Как видно из формулы (2), нормальное напряжение  по высоте сечения изменяется по линейному закону. Максимальное по модулю значение напряжения возникают крайних слоях балки, в точках наиболее удаленных от нейтральной линии поперечного сечения, при max y  y :

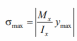
Касательные напряжения при изгибе

Касательное напряжение определяется формулой Журавског:

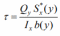
Расчет балки на прочность

Условие прочности при изгибе формулируется следующим образом: максимальное значение нормального напряжения в балке не должно превышать допускаемого напряжения. Следовательно, с учетом формулы для вычисления максимального нормального напряжения

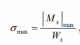
должно выполняться условие прочности

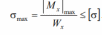
Для хрупких материалов, у которых прочность при сжатии выше, чем при растяжении, допускаемые напряжения на растяжение с  р . Поэтому для хрупких материалов используются два условия прочности:

Наряду с условием прочности (1) при расчете на прочность следует проверять выполнение условие прочности по максимальным касательным напряжениям :

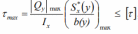
Дифференциальное уравнение изгиба балки и его интегрирование и его граничные условия

дифференциальное уравнение изгиба балки: