11. Энергетические методы. Потенциальная энергия деформации стержня. Теорема Ка-стильяно. Метод Мора.
Потенциальная энергия деформации стержня. Теорема Кастильяно. Метод Мора.
состоит в приближенном определении квадрата частоты собственных колебаний стержня из энергетических соотношений на основании принимаемой заранее приближенной формы упругой линии стержня.
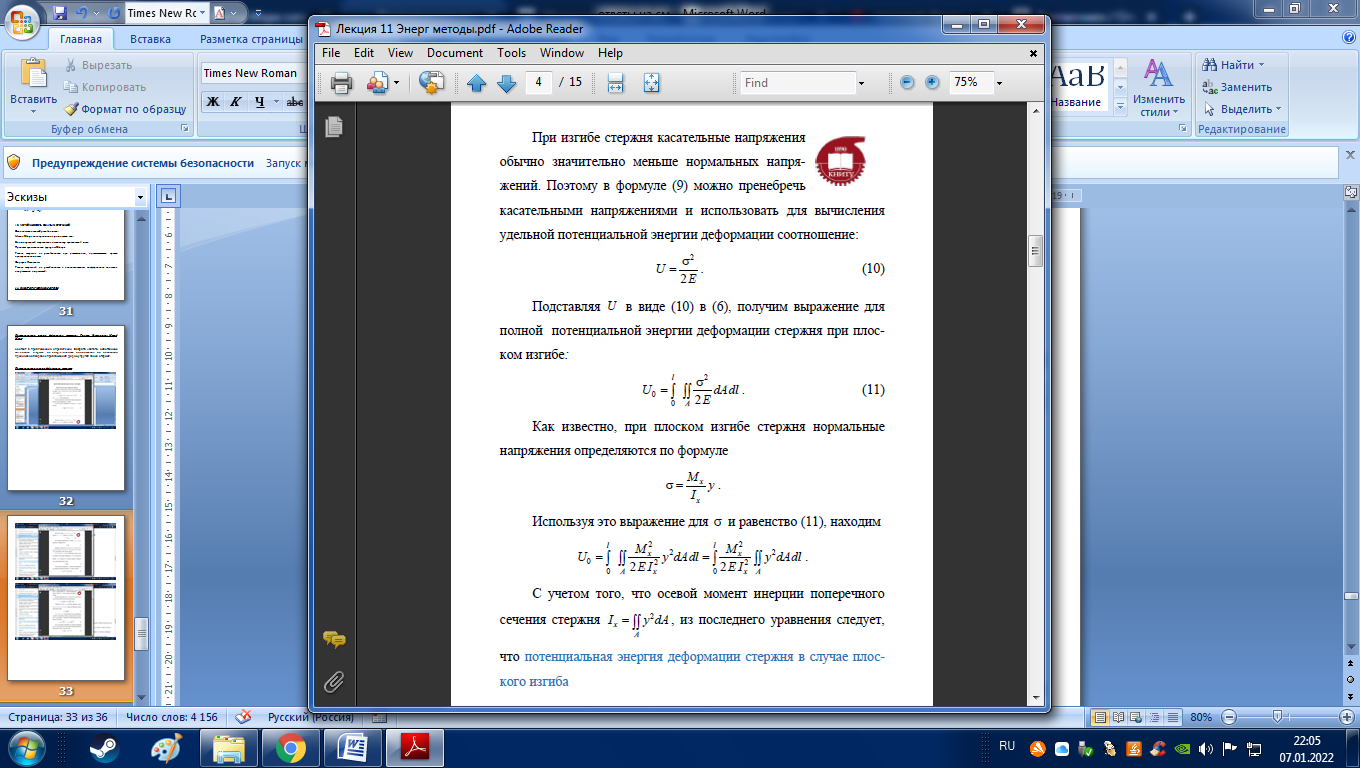
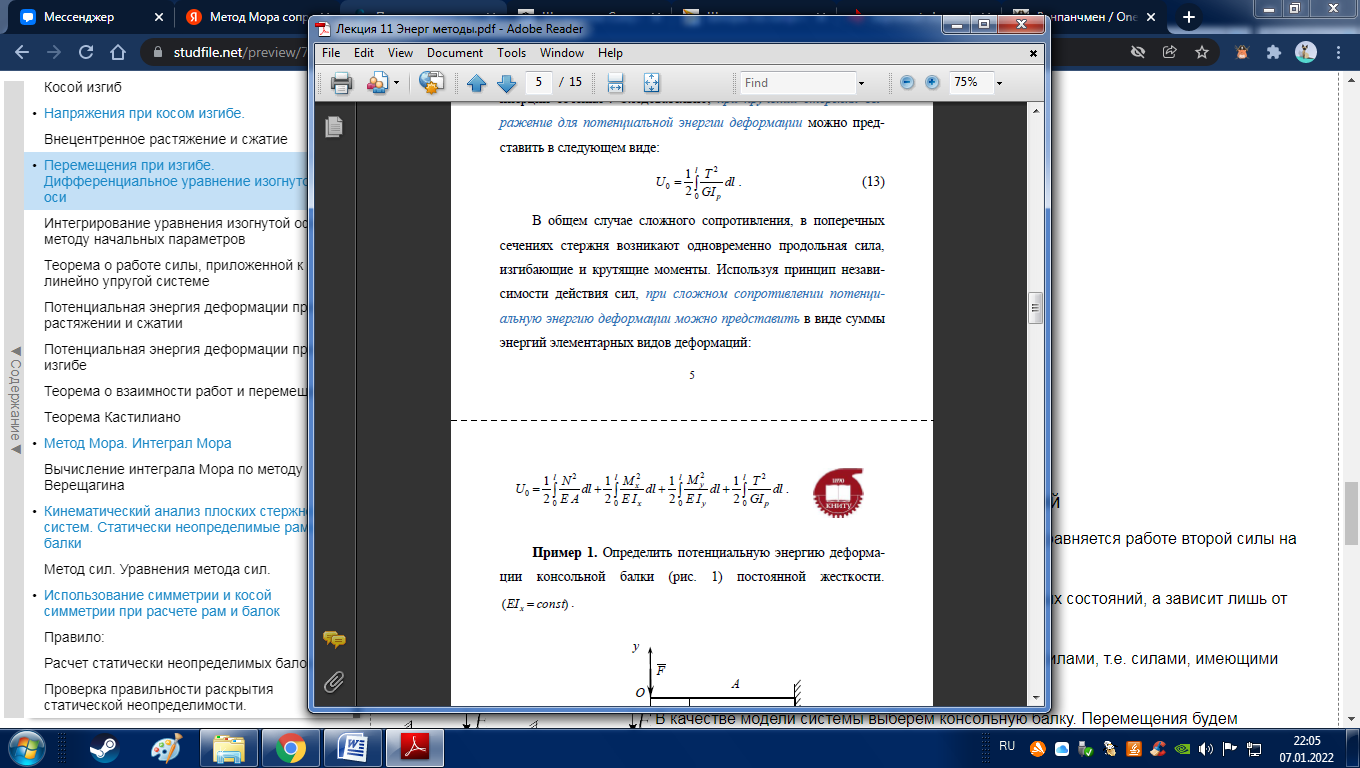
Потенциальная энергия деформации стержня
Теорема Кастильяно
Для определения перемещений стержневой системы может быть использована теорема Кастильяно, которая имеет следующую формулировку: производная от потенциальной энергии деформации упругого тела по силе, равна перемещению точки приложения силы по направлению этой силы.
Перемещение точки тела по направлению силы равна про- екции полного перемещения точки на направление силы.
Метод Мора
Теорема
Кастельяно дала нам возможность
определять перемещения. Эту теорему
используют для отыскания перемещений
в пластинках, о
болочках.
Однако, вычисление потенциальной энергии
громоздкая процедура и мы сейчас наметим
более простой и наиболее общий путь
определения перемещений в стержневых
системах.
Пусть
задана произвольная стержневая система
и нам нужно определить в ней перемещение
точки 
по
направлению 
,
вызванное всеми силами системы -
Т.к.
в общем случае в системе нет силы,
приложенной по направлению искомого
перемещения, то воспользоваться теоремой
Кастельяно нельзя. Добавим к числу
прочих сил силу 
,
приложенную к точке
и
действующую в направлении
.
Тогда внутренние силовые факторы в
системе можно выразить
,
где 
-
внутренние силовые факторы в системе
от действующих сил;
-
внутренние силовые факторы от силы 
.
Внесем
эти выражения в (3) 
По
теореме Кастельяно: 
Учтя,
что 
получаем
выражение: 
называемое интегралом Мора.
Для того, чтобы определить перемещение с помощью метода Мора, необходимо:
1) Определить внутренние силовые факторы в системе от заданных сил.
2) Приложить по направлению искомого перемещения единичную обобщенную силу (единичную силу для определения линейного перемещение, пару сил с моментом равным единице для определения углового перемещения и определить внутренние силовые факторы от единичной силы.
3) Подставить полученные ранее выражения в интеграл Мора и определить перемещение.
Для
систем, работающих на изгиб: балок, рам,
влияние нормальных сил на величину
перемещения незначительно и интеграл
Мора в этом случае выглядит: 
13. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ. Основные понятия. Примеры концентраторов напряжений. Анализ распределений напряжений в простейших конструкциях с концентратором напряжений. Теоретический коэффициент концентрации напряжений. Способы снижения концентрации напряжений.
КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ
называется увеличение напряжений в малых областях, примыкающих к местам с резким изменением формы поверхности тела, размеров его сечения или с локализованной неоднородностью материала внутри тела. Реальные конструкции всегда имеют зоны, в которых проявляется локальная концентрация напряжений.
Основные понятия
Указанные особенности в материале, в форме элемен-тов конструкции, сосредоточенные и резко изменяющиеся нагрузки называются концентраторами напряжений. В окрест-ности концентраторов напряжений возникает быстрое измене-ние напряжений. Явление быстрого возрастания напряжений в окрестности некоторых точек тела называется концентрацией напряжений
Напряжения, возникающие вблизи концентраторов напряжений, не могут быть правильно определены с помощью формул сопротивления материалов или на основе каких-либо других приближенных теорий прочности.
С достаточно большой точностью величины напряжений вблизи концентраторов напряжений определяются экспериментально, либо с использованием науки о деформировании упругих твердых тел – теории упругости.
Номинальное напряжение определяют для наиболее ослабленного сечения.
Концентрация напряжений при растяжении – сжатии, кручении и изгибе
В элементах конструкций, испытывающих деформацию растяжения – сжатия, типичными концентраторами напряжений являются отверстия и переходные галтели.
При кручении касательные напряжения в поперечных сечениях стержня, с учетом концентрации напряжений, определяются по формуле
Примеры концентраторов напряжений
http://www.soprotmat.ru/concentrate.htm
Анализ распределений напряжений в простейших конструкциях с концентратором напряжений
В сечении 3 – 3 размеры стержня резко изменяются и напряжения будут распределяются неравномерно, возрастая к краям верхнего стержня и убывая к середине.
Теоретический коэффициент концентрации напряжений
Способы снижения концентрации напряжений
Для уменьшения или устранения негативного влиянием концентрации напряжений на прочность применяется следующее:
форма элемента конструкции должна изменяться по возможности плавно;
используются уменьшающие концентрацию напряжений способы увеличения, или наоборот, уменьшения размеров деталей в некоторых зонах. Например, усиливают края отверстий и вырезов ребрами жесткости, а для прекращения развития трещины в пластине, на ее концах можно просверлить отверстия, что значительно снизит коэффициент концентрации напряжения;
повышается качество обработки поверхности деталей (шлифование) с целью уменьшения концентра-ции напряжений в микронеровностях;
используется поверхностное упрочнение материала в зоне концентрации напряжений. Для достижения поверхностного упрочнения материала применяются различные способы обра-ботки деталей (термическая обработка, закалка токами высокой частоты, азотирование, обработка давлением с использованием накатки роликом или дробеструйного наклепа).
14. РАСЧЕТ КОНСТРУКЦИЙ НА ВЫНОСЛИВОСТЬ. Понятие об усталостном разрушении. Виды циклов напряжнений. Предел выносливости. Диаграмма предельных амплитуд. Факторы, влияющие на величину предела выносливости
Понятие об усталостном разрушении.
Усталость – разрушение при постоянном развитии трещин. Примерно 90% всех поломок частей машин является следствием развития трещин усталости. Усталостные напряжения – напряжения, переменные по величине и повторяющиеся большое число раз.
Процесс постепенного накопления повреждений в материале при действии переменных во времени напряжений, приводящий к образованию трещин и разрушению, называется усталостным разрушением материала
Виды циклов напряжнений.
Предел выносливости
Предел выносливости (усталости) σR – наибольшее (предельное) напряжение цикла, при котором не происходит усталостного разрушения образца после произвольно большого числа циклов.
Диаграмма предельных амплитуд
Диаграмма
предельных амплитуд вмещает
в себя пределы выносливости для
бесконечного числа разнообразных циклов
напряжений. Детали машин в процессе
эксплуатации испытывают напряжения,
изменяющиеся во времени по самым
разнообразным циклам, характеризуемым
коэффициентом асимметрии (R). Для каждого
такого цикла, в принципе, необходимо
определить свой предел выносливости
материала (
).
В диапазоне от симметричного цикла до постоянного цикла (простого растяжения) укладывается бесконечное количество самых разнообразных циклов. Кроме того, опытное определение для каждого возможного цикла требует большого количества образцов и длительного времени испытаний. Поэтому в лабораторных условиях решить эту задачу полностью невозможно.
Вследствие перечисленных причин по ограниченному числу опытов строится так называемая диаграмма предельных амплитуд (рис. 14.4).
По
оси ординат диаграммы предельных
амплитуд (рис. 14.4) откладывают значение
амплитудного напряжения (
),
а по оси абсцисс – значение среднего
напряжения (
)
предельного цикла. Каждая пара напряжений
на диаграмме предельных амплитуд
и
определяет
соответствующий предельный цикл
(максимальное напряжение (
)
равно пределу выносливости цикла (
)),
который изображается на диаграмме
предельных амплитуд точкой.
Точка
A соответствует симметричному
предельному
циклу. Ее ордината –
,
а абсцисса – 
.
Точка B характеризует предельный
постоянный цикл (
,
)
для хрупкого материала, а точка 
(
,
)
– предельный постоянный цикл для
пластичного материала. Точка C отвечает
предельному отнулевому циклу (
).Таким
образом, кривая AСB характеризует
предельные циклы для хрупких материалов,
а кривая изображение диаграмма предельных
амплитуд сопромат– для пластичных.
Точки, расположенные ниже этих кривых
(внутри диаграммы), представляют собой
безопасные циклы (не приводящие к
разрушению образца).
Факторы, влияющие на величину предела выносливости
