
- •Уравнения статики
- •Деформации при растяжении-сжатии.
- •Испытание материалов на сжатие.
- •Тензор напряжений
- •6. Теории прочности. Основные понятия. Первая, вторая и третья теории прочности. Четвертая (энергетическая) теория прочности. Теория прочности Мора.
- •7. Кручение. Кручение стержня с круглым поперечным сечением. Определение напряжений и угла закручивания. Расчет валов на прочность и жесткость.
- •Расчеты на прочность при изгибе.
- •Дифференциальное уравнение изгиба балки и его интегрирование и его граничные условия
- •9. Сложное сопротивление. Косой изгиб. Определение напряжений и положения нейтральной линии. Расчет на прочность. Изгиб с кручением. Внецентренное действие продольной силы.
- •3. Внецентренное действие продольной силы. Формула σ.
- •11. Энергетические методы. Потенциальная энергия деформации стержня. Теорема Ка-стильяно. Метод Мора.
3. Внецентренное действие продольной силы. Формула σ.

Перенесём Р в ЦТ поперечного сечения, присоединив два изгибающих момента, тогда N = P; Mu = P*Vp; Mv = P*Up.
Нормальные напряжения в этом случае можно найти в результате суперпозиции решений для центрального растяжения и двух прямых изгибов, относительно U,V: σz(u,v) = N/F + (Mu/Ju)*V + (Mv/Jv)*U, где Mu и Mv берутся с учётом знака, т.е. положительные, если вызывают растяжение волокон I координатной четверти.
U и V – координаты той точки на поперечном сечении, для которой вычисляется σ.
Е![]() сли
действуют несколько осевых нагрузок,
то внутренние силы вычисляются по
формулам с учётом знака: N = ∑Pi ;
Mu = ∑Pi*Vpi ;
сли
действуют несколько осевых нагрузок,
то внутренние силы вычисляются по
формулам с учётом знака: N = ∑Pi ;
Mu = ∑Pi*Vpi ;
Mv = ∑Pi*Upi.
10. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ. Основные понятия об устойчивости. Метод Эйлера для определения критических сил. Влияние условий закрепления на величину критической силы. Пределы применимости формулы Эйлера. Расчет стержня на устойчивость при растяжениях, превышающих предел пропорциональности. Формула Ясинского. Расчет стержней на устойчивость с использованием коэффициента снижения допускаемых напряжений.
УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ
называют их способность восстанавливать начальную прямолинейную форму после снятия продольной сжимающей нагрузки
При сжатии длинных стержней их продольная ось искривляется. Такой вид деформации называется продольным изгибом.
Основные понятия об устойчивости
Нагрузка, при которой прямолинейная форма перестает быть формой устойчивого равновесия называется критической (Fкр).
Многие механические системы могут находиться в устойчивом и неустойчивом состояниях. Состояние системы называется устойчивым, если малые возмущающие силы не приводят к существенному изменению ее исходного положения. Состояние системы будет неустойчивым, если малые возмуще-ния приводят к существенному изменению ее исходного поло-жения.

Таким образом, исследование устойчивости стержня заключается в определении величины критической сжимающей силы Fкр.
Для обеспечения устойчивости допускаются нагрузки, составляющие лишь определенную часть от критических и называемые допустимыми силами [F]у.

здесь, nу – коэффициент запаса устойчивости, зависит от материала стержня.
Рекомендуемые значения коэффициента устойчивости находятся в пределах:
для стальных стоек nу=1,5…3;
для деревянных nу=2,5…3,5;
для чугунных nу=4,5…5,5.
Поперечные сечения сжатых стержней должны назначаться не из условия прочности от чистого сжатия, а из условия того, чтобы сжимающие напряжения были меньше критических напряжений:
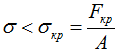
где A – площадь поперечного сечения стержня.
Критическая сила определяется по формуле Эйлера.
Метод Эйлера для определения критических сил




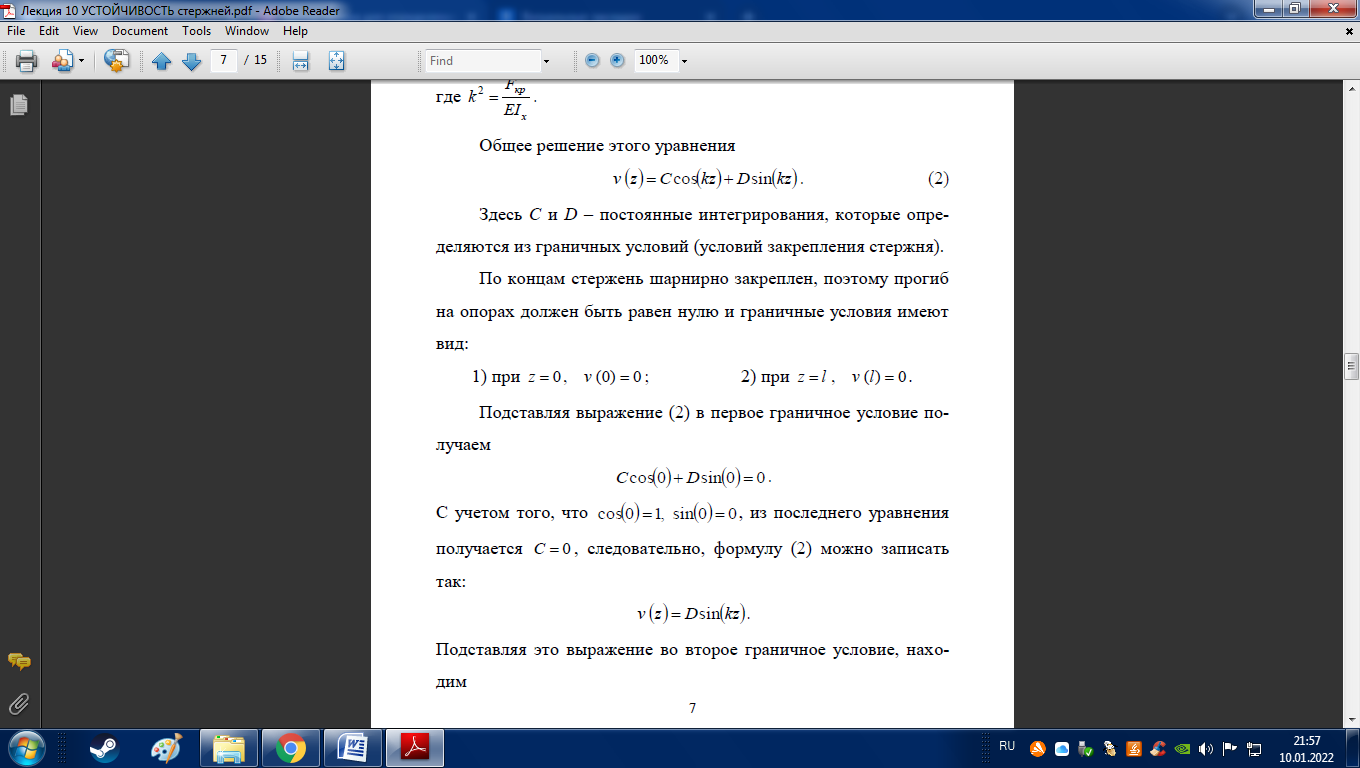





Влияние условий закрепления на величину критической силы
При выводе формулы Эйлера было показано, что в случае достижения внешней силой критического значения, изогнутая ось стержня описывает полуволну синусоиды. Это легко осуществляется при шарнирном закреплении его концов. При других способах закрепления количество полуволн изменяется. Поэтому для общего способа опорных закреплений стержня формулу Эйлера запишем в следующем виде:


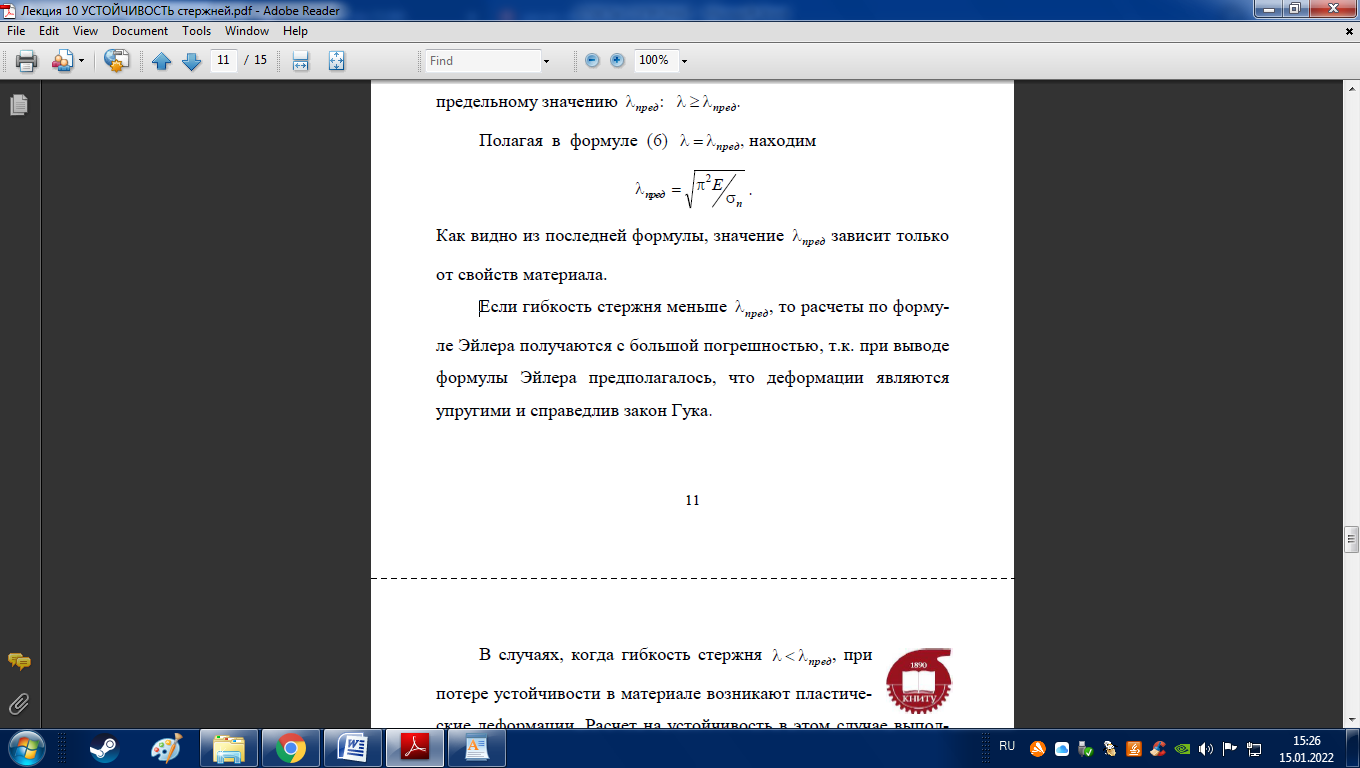
Пределы применимости формулы Эйлера




Расчет стержня на устойчивость при растяжениях, превышающих предел пропорциональности.

https://studref.com/363833/stroitelstvo/poterya_ustoychivosti_napryazheniyah_prevyshayuschih_predel_proportsionalnosti_materiala
https://lfirmal.com/ponyatie-o-potere-ustojchivosti-pri-napryazheniyah-prevyshayushchih-predel-proporcionalnosti/



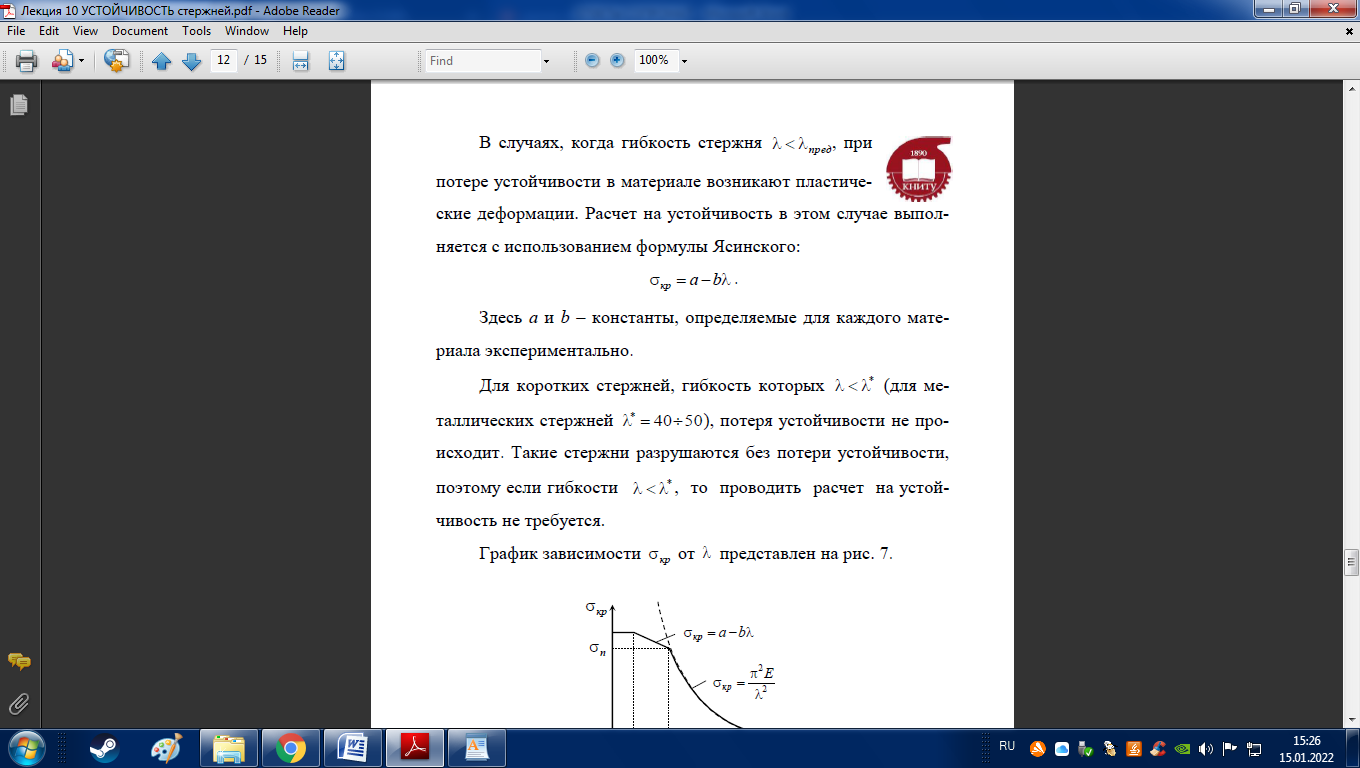
Формула Ясинского

Расчет стержней на устойчивость с использованием коэффициента снижения допускаемых напряжений





