6. Теории прочности. Основные понятия. Первая, вторая и третья теории прочности. Четвертая (энергетическая) теория прочности. Теория прочности Мора.

Основные понятия

Теории прочности представляют собой гипотезы о критериях определяющих условия перехода в опасное состояние.

С увеличением действующей нагрузки увеличиваются и возникающие в теле напряжения, и при некоторых их значениях наступает опасное, или, так называемое, предельное напряженное состояние материала.

Прочность - это способность материалов сопротивляться внутренним напряжениям, возникающим под действием внешних нагрузок.

Первая, вторая и третья теории прочности. Четвертая (энергетическая) теория прочности

Теория прочности Мора

7. Кручение. Кручение стержня с круглым поперечным сечением. Определение напряжений и угла закручивания. Расчет валов на прочность и жесткость.

КРУЧЕНИЕ

Кручение стержня с круглым поперечным сечением

Кручением называется вид нагружения стержня, при котором в его поперечных сечениях возникает единственный внутренний силовой фактор – крутящий момент T .

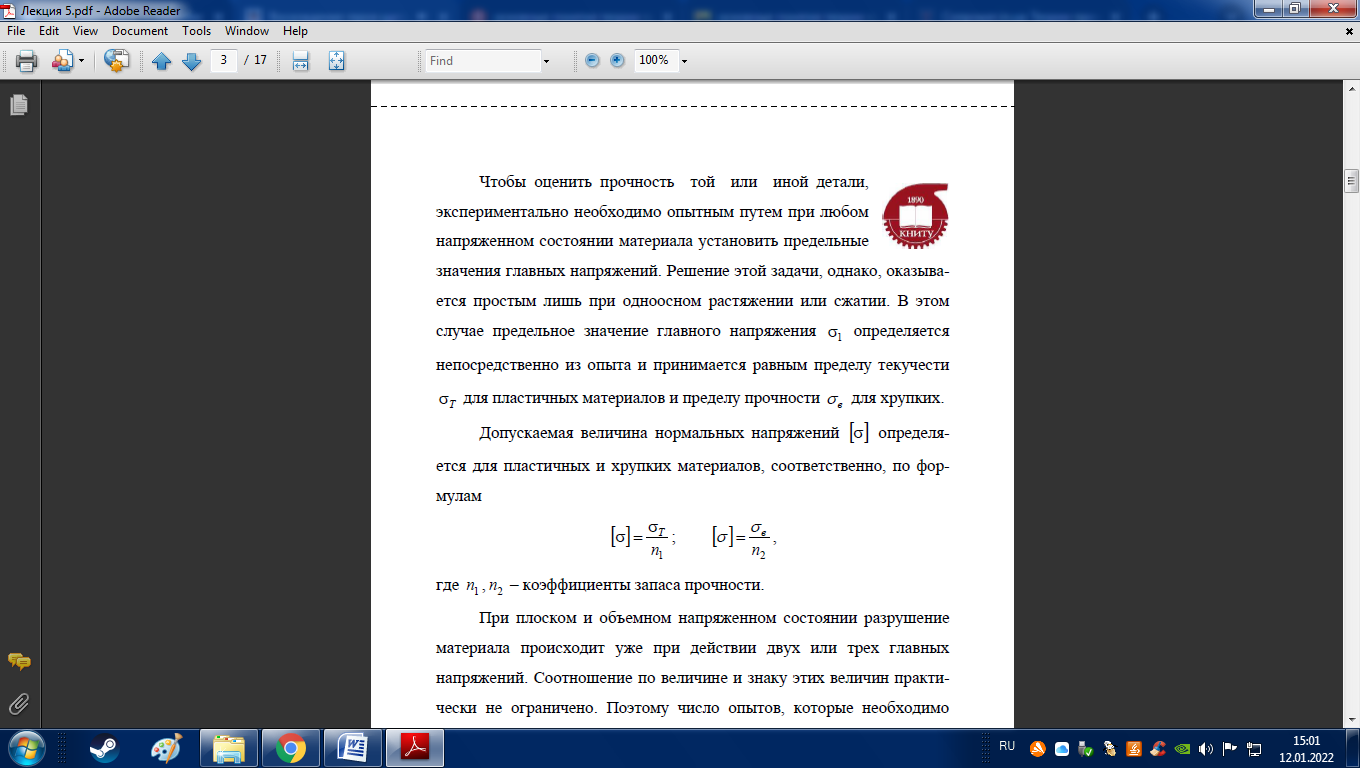
В поперечном сечении вала, расположенном на некотором расстоянии z от торцевого, на элементарной площадке dA будет действовать касательное напряжение  (рис. 2), которое создает относительно оси вала элементарный крутящий момент величиной dT  (dA). Суммируя действующие в сечении элементарные крутящие моменты, получим

Таким образом, касательные напряжения при кручении прямо пропорциональны расстоянию от центра тяжести сечения до рассматриваемой точки

Наибольшие напряжения возникают в точках контура сечения при  = R:

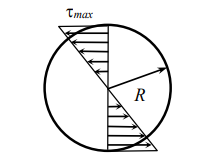
Максимальное касательное напряжение, возникающее в опасном сечении вала, не должно превышать допускаемого напряжения [] . Следовательно, условие прочности при кручении имеет вид

Определение напряжений и угла закручивания

Угол закручивания, приходящийся на единицу длины, называют относительным углом закручивания:

Для обеспечения требуемой жесткости вала необходимо, чтобы наибольший относительный угол закручивания не превосходил допускаемого:

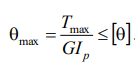
Эта формула выражает условие жесткости вала при кручении.

Расчет валов на прочность и жесткость

Расчет вала при кручении сводится к одновременному удовлетворению двух условий:

-условие прочности

-условие жесткости

8. ИЗГИБ. Плоский изгиб балок. Чистый изгиб. Нормальные напряжения при чистом изгибе. Касательные напряжения при изгибе. Расчет балки на прочность. Дифференциальное уравнение изгиба балки и его интегрирование. Граничные условия.

Изгибом называется вид деформации, при котором искривляется продольная ось бруса. Прямые брусья, работающие на изгиб, называются балками. Прямым изгибом называется изгиб, при котором внешние силы, действующие на балку, лежат в одной плоскости (силовой плоскости), проходящей через продольную ось балки и главную центральную ось инерции поперечного сечения.

Плоский изгиб балок. Чистый изгиб.

Изгиб называется чистым, если в любом поперечном сечении балки возникает только один изгибающий момент.

Изгибом называется вид нагружения стержня, при котором в его поперечном сечении возникает изгибающий момент. Стержень, при изгибе, называется балкой.

Плоский изгиб – изгиб, при котором все усилия, изгибающие балку, лежат в одной из плоскостей симметрии балки (в одной из главных плоскостей).

Изгиб называется плоским, если Мх  0 и Qy  0 , а М y  Qх  N  T  0 .

Нормальные напряжения при чистом изгибе.

 при изгибе продольные слои балки не взаимодействуют друг с другом в перпендикулярных к ним направлениях, Из этого предположения следует, что в любой точке балки х  у  0 ;

 поперечные сечения балки, плоские до деформации, после деформации остаются плоскими и перпендикулярными к продольной оси (гипотеза плоских сечений);

 напряжения в поперечных сечениях балки не изменяются по его ширине.

Кроме того, полагается, что связь между напряжением и деформацией определяется законом Гука   Е ,

формулу для определения нормальных напряжений в сечениях стержня при чистом изгибе:

Как видно из формулы (2), нормальное напряжение  по высоте сечения изменяется по линейному закону. Максимальное по модулю значение напряжения возникают крайних слоях балки, в точках наиболее удаленных от нейтральной линии поперечного сечения, при max y  y :

Касательные напряжения при изгибе.

Расчет балки на прочность