Тензор напряжений

При анализе напряжений в окрестности рассматриваемой точки выделяется бесконечно малый объемный элемент (параллелепипед со сторонами dx, dy, dz), по каждой грани которого действуют, в общем случае, три напряжения, например, для грани, перпендикулярной оси x (площадка x) – σx xy xz

Компоненты напряжений по трем перпендикулярным граням элемента образуют систему напряжений, описываемую специальной матрицей – тензором напряжений

Здесь первый столбец представляет компоненты напряжений на площадках, нормальных к оси x, второй и третий – к оси y и z соответственно.

При повороте осей координат, совпадающих с нормалями к граням выделенного элемента, компоненты напряжений изменяются. Вращая выделенный элемент вокруг осей координат, можно найти такое положение элемента, при котором все касательные напряжения на гранях элемента равны нулю.

Площадка, на которой касательные напряжения равны нулю, называется главной площадкой.

Нормальное напряжение на главной площадке называется главным напряжением

Нормаль к главной площадке называется главной осью напряжений .

В каждой точке можно провести три взаимно-перпендикулярных главных площадки.

При повороте осей координат изменяются компоненты напряжений, но не меняется напряженно-деформированное состояние тела (НДС).

Виды напряженных состояний

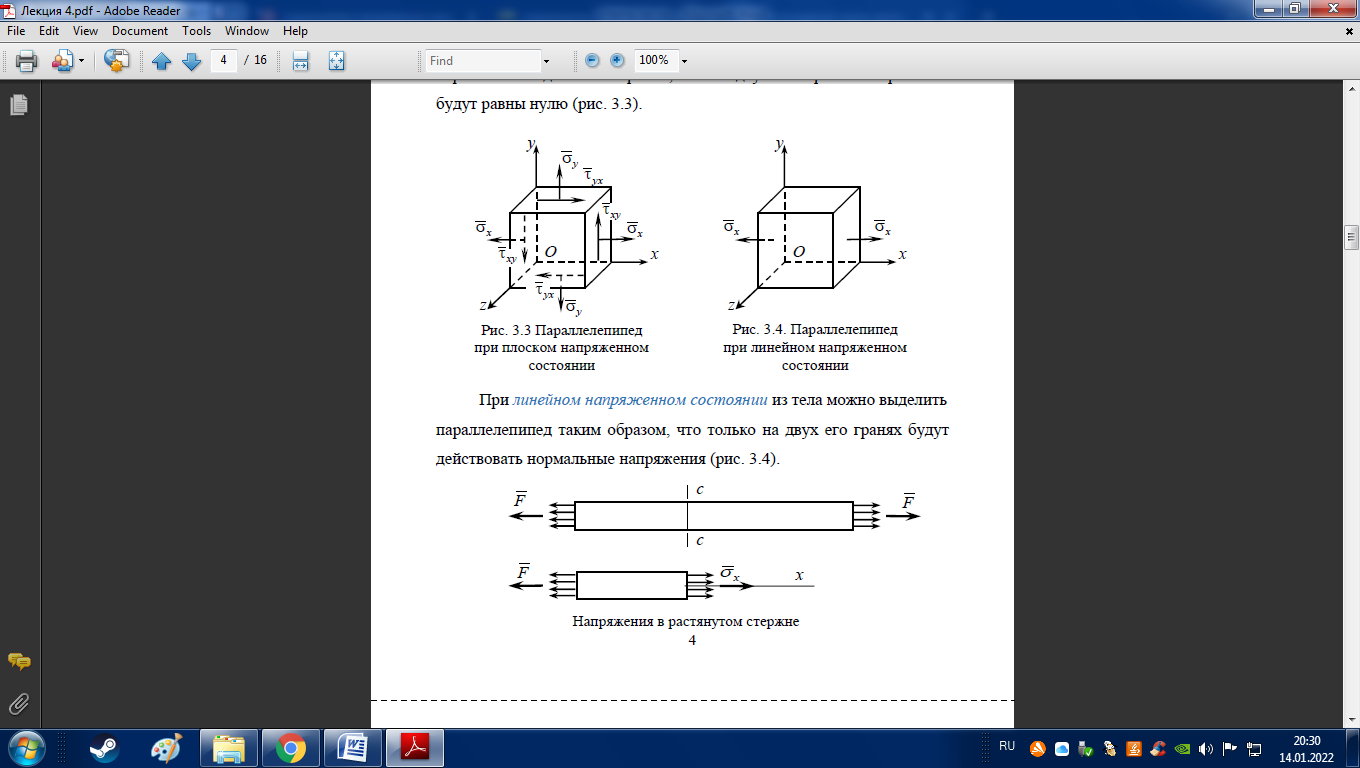
Плоское напряженное состояние

Напряженное состояние называется плоским или двухосным, если одно из главных напряжений равно нулю (рис. 3.3).

Рис.3.3

Напряжения на наклонной площадке (рис. 3.4,а)

Величина и направление главных напряжений (рис. 3.4,б)

Чистый сдвиг σ_x = σ_y = 0   (рис. 3.4,в)

……………………………………………………….

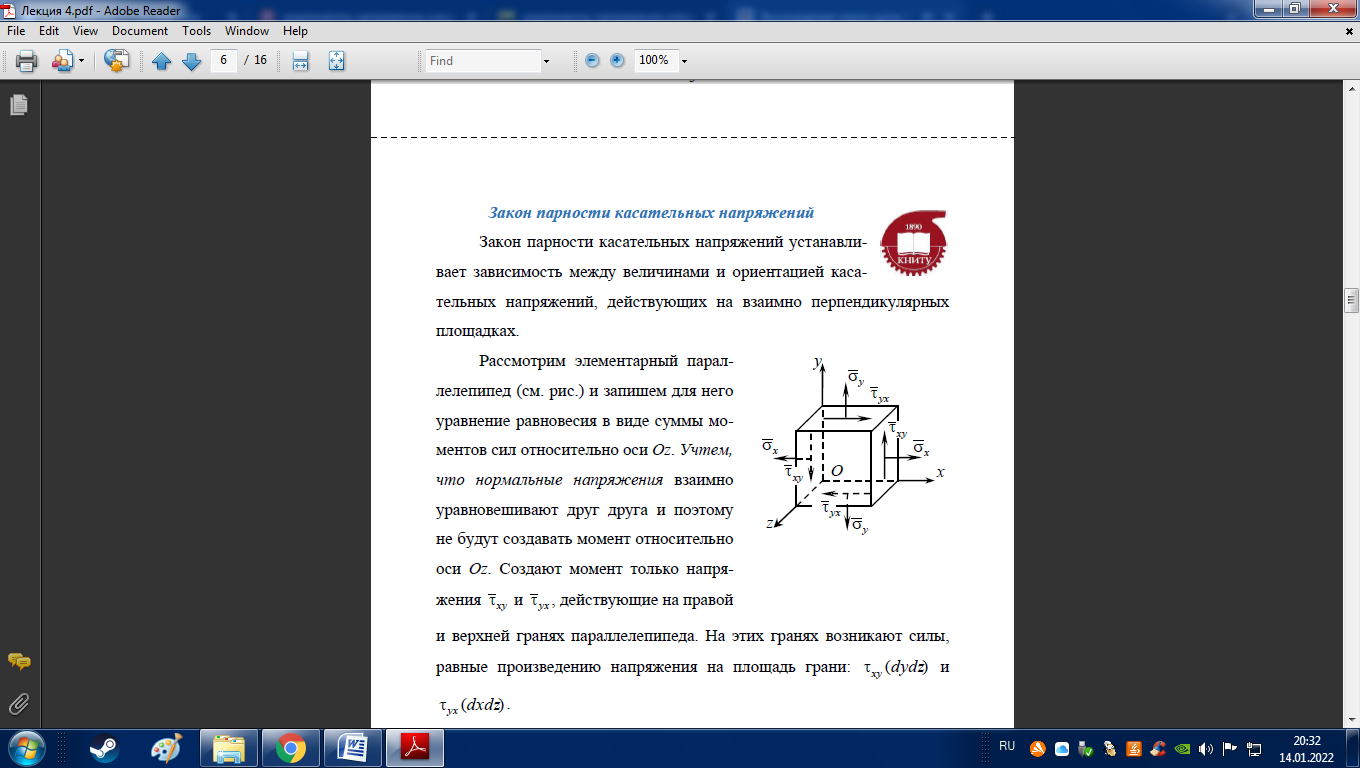
Закон парности касательных напряжений

Напряжения на наклонных площадках

Главные напряжения

Площадки, на которых отсутствуют касательные напряжения, называются главными площадками, а нормальные напряжения, действующие по этим площадкам, — главными напряжениями.

Максимальные касательные напряжения

Чистый сдвиг. Закон Гука при сдвиге

Напряженное состояние, при котором по граням параллелепипеда действуют только касательные напряжения, называется чистым сдвигом.

Чистый сдвиг возникает при кручении стержней и при деформировании заклепочных соединений.

Деформированное состояние в точке

Деформированное состояние в точке. В любой точке тела можно выделить отрезки dx, dy, dz параллельные осям координат и определить перемещения u, v, w, линейные деформации  x,  y,  z, а также изменения углов между этими отрезками – угловые деформации  xy,  xz,  yz. Совокупность перемещений u, v, w, линейных  x,  y,  z и угловых  xy,  xz,  yz деформаций определяет деформированное состояние тела в точке.

Обобщенный закон Гука. Компоненты деформации

Обобщенный закон Гука представляет собой связь между напряжениями и деформациями в случае объемного напряженного со- стояния. Этот закон может быть получен с использованием принципа независимости действия сил, на основании закона Гука при растяжении-сжатии стержня и при чистом сдвиге.

Потенциальная энергия деформации

Потенциальной энергией деформации называется энергия, которая накапли-

вается в теле при его упругом деформировании.

напряжением τ и углом сдвига 

При чистом сдвиге потенциальная энергия изменения объема равна нулю,

Потенциальная энергия численно равняется работе внешних сил:

. (11.12)

Учитывая, что  , , выражение для потенциальной энергии получим в виде: