Деформации при растяжении-сжатии.

Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l₁ и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением, или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).

Коэффициент Пуассона. Закон Гука.

Законом Гука: нормальное напряжение в поперечном сечении прямо пропорционально деформации: ,

𝝴-деформация, Е- модуль нормальной упругости(модуль Юнга)

По определению коэффициент Пуассона численно равен отношению поперечной деформации к продольной, взятому по абсолютной величине:

Модуль упругости.

Модуль упругости — коэффициент пропорциональности в законе Гука, характеризующих способность тел мгновенно восстанавливать свою форму и объем после прекращения действия внешних сил

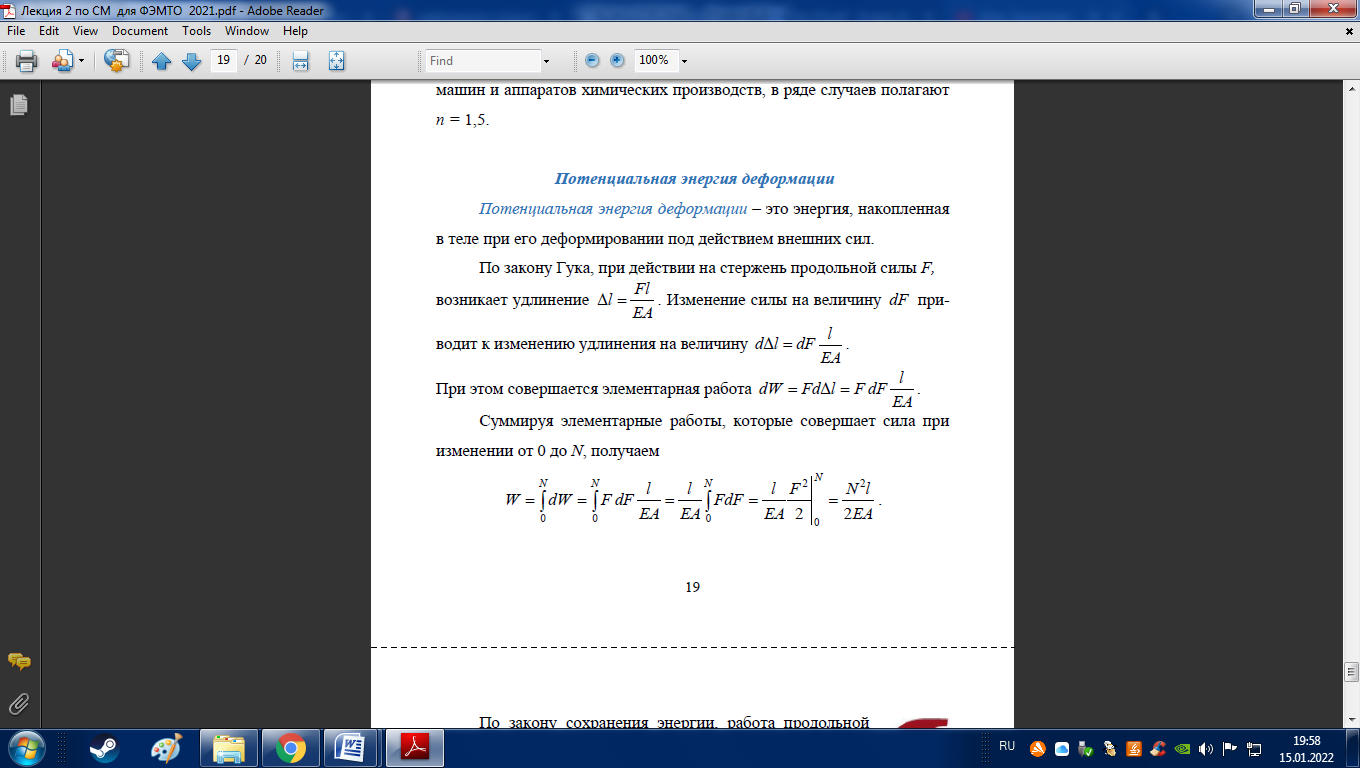
Потенциальная энергия деформации

Испытание материалов на растяжение-сжатие. Диаграммы на растяжение-сжатие различных материалов.

Некоторые свойства материалов проявляются при испытаниях образцов из этих материалов на растяжение. На основе этих экспериментов определяются механические характеристики материалов, позволяющие оценить их прочностные и пластические свойства.

Для проведения опытов на растяжение используют специально изготовленные образцы (рис. 2.5), которые закрепляются в захватах машины и растягиваются вплоть до разрушения. При этом зависимость между растягивающей силой F и удлинением образца l записывается в виде графика (рис. 2.6), который называется машинной диаграммой растяжения материала.

Рассмотрим диаграмму растяжения образца из малоуглеродистой стали (рис. 2.7). На этой диаграмме отмечены точки А, В, С, D.

Точке А соответствует напряжение п – предел пропорциональности.

Вблизи точки А, на криволинейном участке диаграммы, можно отметить точку В, соответствующую пределу упругости у .

Начиная от точки С, диаграмма имеет горизонтальный (или почти горизонтальный) участок, которому соответствует предел текучести т . На этом участке деформации растут без увеличения нагрузки.

Горизонтальный участок диаграммы CD называют площадкой текучести. Площадка текучести ярко выражена только для малоуглеродистых сталей. Ее возникновение связано с явлением текучести в материале. Точке Е на диаграмме соответствует напряжение в – предел прочности.

До достижения предела прочности в продольные и поперечные деформации образца равномерно распределяются по его длине.

После достижения точки Е диаграммы, образец в основном деформируется в окрестности одного наиболее ослабленного сечения, где начинает образовываться шейка – значительное сужение образца. Образец до деформации и после образования шейки показан на рис. 2.8.

За точкой Е нагрузка снижается, что объясняется уменьшением поперечного сечения шейки. Разрыву образца на диаграмме соответствует точка S.

К прочностным характеристикам материала относятся предел пропорциональности п , предел упругости у , предел текучести т , предел прочности в (временный предел прочности).

Пластичность материала характеризуется относительным остаточным удлинением при разрыве  и относительным остаточным поперечным сужением при разрыве .

В зависимости от величин δ и , конструкционные материалы условно делятся на пластичные и хрупкие. Материал считается пластичным, если относительная остаточная деформация  больше 5 %.

Хрупкие материалы разрушаются без образования заметных остаточных деформаций. К ним относятся чугун, стекло, кирпич, строительные камни. Величина удлинения δ при разрыве не превышает 2… 5%.

Пластичные материалы при нагружении способны образовывать большие остаточные деформации. К ним относятся медь, латунь, алюминий.