Оглавление

1. ВВЕДЕНИЕ Курс сопротивления материалов. Прочность, жесткость и устойчивость элементов конструкций. Основные гипотезы, принимаемые в курсе сопротивления материалов. Реальный объект и расчетная схема. Схематизация элементов конструкций (стержень, пластина, оболочка, массивное тело). Виды внешних сил. Объемные и поверхностные нагрузки. Виды опор. Опорные реакции. Уравнения статики. 3

Уравнения статики 9

2. ВНУТРЕННИЕ СИЛЫ. Метод сечений. Внутренние силовые факторы в поперечном сечении стержней. Продольная сила. Построение эпюр продольных сил. Крутящий момент. Построение эпюр крутящих моментов. Плоский изгиб. Построение эпюр изгибающего момента и поперечной силы. 12

Дифференциальные зависимости при изгибе. Правила проверки правильности построения эпюр. Понятие о напряженном состоянии в точке. Полное, нормальное и касательное напряжения. Интегральная связь между напряжениями и внутренними силовыми факторами. Понятие о деформированном состоянии в точке. Линейные и угловые деформации. 12

3. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ. Растяжение и сжатие прямолинейного стержня. Напряжения в поперечных сечениях. Деформации при растяжении-сжатии. Коэффициент Пуассона. Закон Гука. Модуль упругости. Потенциальная энергия деформации. Испытание материалов на растяжение-сжатие. Диаграммы на растяжение-сжатие различных материалов. Механические характеристики материалов. Пластичные и хрупкие материалы. Допускаемые напряжения, коэффициент запаса прочности. Условие прочности при растяжении-сжатии. 27

Деформации при растяжении-сжатии. 29

4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ ФИГУР. Основные геометрические характеристики плоских фигур. Статический момент инерции, определение центра тяжести фигуры. 41

Осевой, полярный и центробежный моменты инерции фигур. Моменты инерции простейших фигур. Изменения геометрических характеристик при параллельном переносе осей координат. Изменения моментов инерции при повороте осей координат. Главные оси и главные моменты инерции. 41

5. ОСНОВЫ ТЕОРИИ НАПРЯЖЕННОГО-ДЕФОРМИРОВАННОГО СОСТОЯНИЯ. Напряженное состояние в точке. Компоненты напряжения. Виды напряженных состояний. Плоское напряженное состояние. Закон парности касательных напряжений. 49

Напряжения на наклонных площадках. Главные напряжения. Максимальные касательные напряжения. Чистый сдвиг. Закон Гука при сдвиге. Деформированное состояние в точке. Компоненты деформации. Обобщенный закон Гука. Потенциальная энергия деформации. 49

Тензор напряжений 52

6. ТЕОРИИ ПРОЧНОСТИ. Основные понятия. Первая, вторая и третья теории прочности. Четвертая (энергетическая) теория прочности. Теория прочности Мора. 71

7. КРУЧЕНИЕ. Кручение стержня с круглым поперечным сечением. Определение напряжений и угла закручивания. Расчет валов на прочность и жесткость. 75

8. ИЗГИБ. Плоский изгиб балок. Чистый изгиб. Нормальные напряжения при чистом изгибе. Касательные напряжения при изгибе. Расчет балки на прочность. Дифференциальное уравнение изгиба балки и его интегрирование. Граничные условия. 79

Расчеты на прочность при изгибе. 82

9. Сложное сопротивление. Косой изгиб. Определение напряжений и положения нейтральной линии. Расчет на прочность. Изгиб с кручением. Внецентренное действие продольной силы. 84

Определение напряжений при косом изгибе 87

10. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ. Основные понятия об устойчивости. Метод Эйлера для определения критических сил. Влияние условий закрепления на величину критической силы. Пределы применимости формулы Эйлера. Расчет стержня на устойчивость при растяжениях, превышающих предел пропорциональности. Формула Ясинского. Расчет стержней на устойчивость с использованием коэффициента снижения допускаемых напряжений. 97

11. ЭНЕРГЕТИЧЕСКИЕ МЕТОДЫ. Потенциальная энергия деформации стержня. Теорема Ка-стильяно. Метод Мора. 114

13. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ. Основные понятия. Примеры концентраторов напряжений. Анализ распределений напряжений в простейших конструкциях с концентратором напряжений. Теоретический коэффициент концентрации напряжений. Способы снижения концентрации напряжений. 121

14. РАСЧЕТ КОНСТРУКЦИЙ НА ВЫНОСЛИВОСТЬ. Понятие об усталостном разрушении. Виды циклов напряжнений. Предел выносливости. Диаграмма предельных амплитуд. Факторы, влияющие на величину предела выносливости 130

1. ВВЕДЕНИЕ Курс сопротивления материалов. Прочность, жесткость и устойчивость элементов конструкций. Основные гипотезы, принимаемые в курсе сопротивления материалов. Реальный объект и расчетная схема. Схематизация элементов конструкций (стержень, пластина, оболочка, массивное тело). Виды внешних сил. Объемные и поверхностные нагрузки. Виды опор. Опорные реакции. Уравнения статики.

Курс сопротивления материалов

Сопротивление материалов является одним из разделов науки о прочности, в котором излагаются закономерности деформирования и разрушения тел, основанные на теоретических исследованиях и данных экспериментов.

Прочность, жесткость и устойчивость элементов конструкций

Прочность – это свойство конструкции сопротивляться разрушению при действии на нее внешних сил (нагрузок).

Жесткость – свойство конструкции сопротивляться деформированию. Конструкция считается жесткой, если при действии внешних сил изменения ее размеров и формы сравнительно малы.

Устойчивость – свойство системы сохранять свое начальное равновесное положение при малых внешних воздействиях, не учитываемых в расчете.

Основные гипотезы, принимаемые в курсе сопротивления материалов

Деформацией называется изменение взаимного расположения частиц тела, вызывающее изменение его размеров и формы. Если си-лы, вызывающие деформацию, постепенно уменьшать и затем полно-стью снять, то тело будет стремиться приобрести свою первоначаль-ную форму. Деформации полностью или частично исчезнут.

Свойство тел деформироваться под нагрузкой и затем после устранения сил восстанавливать свою первоначальную форму, назы-вается упругостью. Часть деформации, которая исчезает после снятия нагрузки, называется упругой деформацией, а та часть, которая остает-ся, называется остаточной деформацией. Возникновение остаточной деформации связано с так называемой пластичностью тела. Если де-формации после снятия нагрузки полностью исчезли, то тело называ-ют абсолютно упругим.

У некоторых материалов упругие свойства одинаковы во всех направлениях. Такие тела называются изотропными. Анизотропным называется тело, у которого упругие свойства различны в разных направлениях.

Если деформации являются упруги-ми, то используется принцип независимости действия сил (принцип суперпозиции). В соответствии с этим принципом – результат сов-местного действия нескольких сил равен сумме результатов от дей-ствия каждой из сил в отдельности.

Полагается, что возникающие в теле деформации и перемещения являются малыми. Кроме того, принимаются предположения, позво-ляющие значительно упростить расчеты:

 принцип Сен-Венана (принцип локальности) – на достаточном удалении от места приложения силы, особенности способа приложе-ния этой силы можно не учитывать;

 гипотеза Бернулли (гипотеза плоских сечений) – поперечные се-чения стержня, плоские и нормальные к оси стержня до деформации, остаются плоскими и нормальными к его оси и после деформации.

Реальный объект и расчетная схема

Расчетная схема – это упрощенное изображение реальной конструкции, которое освобождено от ее несущественных, второстепенных особенностей и которое принимается для математического описания и расчета.

Реальный объект – исследуемый элемент конструкции, взятый с учетом всех своих особенностей: геометрических, физических, механических и других.

Моделью конструкции принято называть вспомогательный объект, заменяющий реальную конструкцию, представленную в наиболее общем виде.

Схематизация элементов конструкций (стержень, пластина, оболочка, массивное тело)

Стержнем называется тело, длина которого значительно боль-ше его поперечных размеров. Геометрическое место точек, совпадающих с центрами тяжести поперечных сечений стержня, называется продольной осью.

Элемент конструкции, ограниченный с двух сторон плоскостями, расстояние между которыми мало по сравнению с другими разм-рами, называется пластиной (рис. 1.1б). Элемент конструкции, ограниченный двумя поверхностями, отстоящими друг от друга на малом расстоянии, называется оболочкой (рис. 1.1в). Элемент конструкции, размеры которого во всех направлениях сравнимы по величине, называется массивом (рис. 1.1г).

Виды внешних сил. Объемные и поверхностные нагрузки.

Внешние силы являются мерой взаимодействия рассматриваемого тела с окружающими телами и средой. Различают объемные и поверхностные силы. Объемные силы непрерывно распределены по всему объему тел. Отметим, что к поверхностным силам относятся вес тела, силы инерции, магнитные силы. Поверхностные силы действуют на поверхности тела.

Динамические нагрузки изменяются во времени быстро, при этом в деформируемой конструкции возникают силы инерции, которые необходимо учитывать при расчетах, так как они достигают значительных величин.

Статические нагрузки являются постоянными, либо медленно изменяют свою величину или точку приложения (направление).

Если размеры площадки, по которой происходит взаимодействие тел, малы по срав-нению с размерами тела, то считается, что поверхностная сила прило-жена в точке и называется сосредоточенной.

Соприкосновение тел всегда происходит по некоторой площад-ке. Поэтому все поверхностные силы являются распределенными по площади.

Виды опор

шарнирно подвижные опоры. Поперечное сечение стержня в шарнирно подвижной опоре может смещаться параллельно опорной плоскости и поворачиваться, но не может смещаться перпендикулярно к опорной плоскости. Поэтому в шарнирно подвижной опоре возникает реакция опоры АR , направленная перпендикулярно к плоскости.

шарнирно неподвижная опора. Поперечное сечение стержня, проходящее через шарнирно неподвижную опору, не может смещаться поступательно. В опоре возникает сила реакции R (рис. 1.5). Ее составляющими являются вертикальная сила B R , препятствующая вертикальному смещению, и горизонтальная сила B H, исключающая горизонтальное смещение закрепленного сечения бруса

Заделка (защемление), это такое закрепление стержня, при котором в месте крепления он не может перемещаться поступательно и поворачиваться.

Опорные реакции

Воздействие закрепляющего элемента на стержень можно заме-нить силой, которая называется реакцией опоры.

Реакция опоры или опорная реакция – это силовой фактор, возникающий в опоре, от действия на конструкцию внешней нагрузки. В опорах, как правило, возникают реактивные силы, которые для удобства ручного расчета раскладываются на две составляющие: вертикальную и горизонтальную проекции.

Уравнения статики

Ранее были показаны примеры составления уравнений равновесия для пространственной и плоской систем сил.

При плоском поперечном изгибе можно записать только два уравнения. Это частный случай плоского нагружения. В этом случае все силы приложенные к балке расположены нормально к ее оси, т. е. не дают проекций на ось балки.

В результате имеем следующие уравнения статики:

1. Сумма проекций всех сил на вертикальную ось равна нулю

2. Сумма моментов относительно любой точки системы тоже равна нулю.

Эти уравнения являются уравнениями равновесия рассматриваемой балки находящейся под действием комплекса нагрузок.

Рассмотрим пример плоского поперечного изгиба, когда все внешние силы имеют исключительно вертикальное направление.

Уравнения статики

Сумма проекций всех сил на ось Y:

Здесь силы и нагрузки записаны в соответствии с правилом знаков для проекций сил.

Равнодействующая распределенной нагрузки определяется произведением ее интенсивности на длину.

Проекции сил на ось Z в данном случае равны нулю:

Сумма моментов всех нагрузок, например, относительно точки A:

Для плоской системы нагружения, при определении опорных реакций и внутренних силовых факторов исходя из условия равновесия системы, можно составить только три уравнения статики.

В общем случае в поперечном сечении будут действовать шесть сил: –N продольная сила (проекция вектора R направленная по оси Оz); , Оx, Оy – поперечные силы (проекции вектора R направленные по осям Оx, Оy); – T крутящий момент (проекция момента отно- сительно оси Оz); , M x M y – изгибающие моменты (проекции момен- та M относительно осей Оx, Оy).

Так как рассматриваемая часть тела находится в равновесии, то должны выполняться шесть уравнений равновесия:

Для наглядного представления о распределении внутренних сил по длине стержня строят графики внутренних сил, которые называют эпюрами внутренних сил.

2. ВНУТРЕННИЕ СИЛЫ. Метод сечений. Внутренние силовые факторы в поперечном сечении стержней. Продольная сила. Построение эпюр продольных сил. Крутящий момент. Построение эпюр крутящих моментов. Плоский изгиб. Построение эпюр изгибающего момента и поперечной силы.

Дифференциальные зависимости при изгибе. Правила проверки правильности построения эпюр. Понятие о напряженном состоянии в точке. Полное, нормальное и касательное напряжения. Интегральная связь между напряжениями и внутренними силовыми факторами. Понятие о деформированном состоянии в точке. Линейные и угловые деформации.

Метод сечений. Сущность его заключается в том, что тело, находящееся в равновесии, рассекают мысленно на две части (рис. 1, а), отбрасывают одну из частей, заменяя влияние отброшенной части внутренними силами, и составляют уравнения равновесия для оставшейся части, на которую действуют приложенные к ней внешние силы1 и подлежащие определению внутренние силы, распределенные по сечению

Внутренние силовые факторы в поперечном сечении стержней.

Внутренние силовые факторы (усилия) возникают в результате деформации бруса, когда под действием внешних нагрузок происходит изменение взаимного расположения элементарных частиц тела.

Продольная сила.

это внутренний силовой фактор, который возникает в поперечных сечениях элементов, работающих на центральное растяжение (сжатие)

N равна проекции главного вектора на ось x. Ее величину численно определяют как алгебраическую сумму проекций на эту ось всех внешних сил (активных и реактивных), приложенных к рассматриваемой части.

Построение эпюр продольных сил.

проводим прямую, параллельную продольной оси бруса (базовая линия). Значение нормальных сил откладывают в выбранном масштабе и с учетом знаков (положительные силы откладываем вправо от базовой линии, а отрицательные — влево) на уровне соответствующего участка.

Крутящий момент. Построение эпюр крутящих моментов.

Т и изгибающие моменты M_z и M_y – проекции главного момента на оси x, y, z – соответственно. Численно каждый из них равен алгебраической сумме моментов относительно соответствующей оси всех внешних сил, приложенных к рассматриваемой части.

Внутренние силы и моменты в разных сечениях стержня различны. Графики, показывающие изменение внутренних усилий вдоль оси стержня, называют эпюрами. При построении эпюр придерживаются следующих правил:

– ось (базу), на которой строится эпюра, выбирают так, чтобы она была параллельна оси стержня;

– ординаты эпюры с выбранным интервалом откладывают от оси по перпендикуляру в избранном масштабе, в характерных сечениях проставляют числа, показывающие величины силового фактора;

– в поле эпюры в кружочке ставят знак усилия.

Плоский изгиб.

изгиб, при котором все усилия, изгибаю-щие балку, лежат в одной из плоскостей симметрии балки (в одной из главных плоскостей).

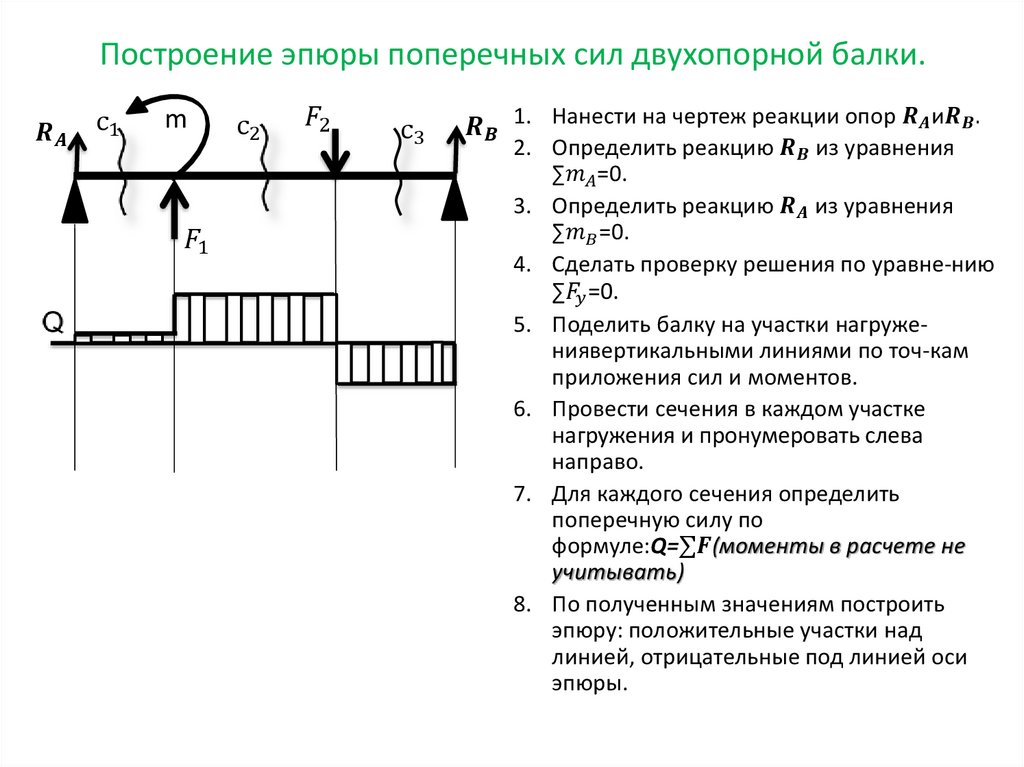
Построение эпюр изгибающего момента и поперечной силы.

Эпюрами внутренних поперечных сил и изгибающих моментов называют графическое представление распределения функций Q и M по длине балки при изгибе.

Для того, чтобы произвести расчет балки на изгиб, необходимо знать величину наибольшего изгибающего момента М и положение сечения, в котором он возникает. Точно также, надо знать и наибольшую поперечную силу Q. Для этой цели строят эпюры изгибающих моментов и поперечных сил. По эпюрам легко судить о том, где будет максимальное значение момента или поперечной силы.

Для определения внутренних сил применяется метод сечений, который заключается в следующем. Находящееся в равновесии под

действием системы внешних сил призматическое тело (рис. 1.7а) рас- секается (мысленно) плоскостью, перпендикулярной к продольной оси, на две части. Одна из частей отбрасывается и рассматривается равновесие оставшейся части. Действие отброшенной части на остав- шуюся заменяется некоторыми распределенными по сечению силами. Как известно, система сил может быть приведена к главному вектору и главному моменту. Распределенные по сечению силы заменяются

Вводится ортогональная система координат, так чтобы ось Оz совпадала с продольной осью тела, а оси Оx и Оy – расположены в по- перечном сечении. Главный вектор и главный момент раскладываются на составляющие, которые называются внутренними силами.

В общем случае в поперечном сечении будут действовать шесть сил: –N продольная сила (проекция вектора R направленная по оси Оz); , Оx, Оy – поперечные силы (проекции вектора R направленные по осям Оx, Оy); – T крутящий момент (проекция момента отно- сительно оси Оz); , M x M y – изгибающие моменты (проекции момен- та M относительно осей Оx, Оy).

Так как рассматриваемая часть тела находится в равновесии, то должны выполняться шесть уравнений равновесия:

Для наглядного представления о распределении внутренних сил по длине стержня строят графики внутренних сил, которые называют эпюрами внутренних сил.

Для построения эпюр балка разбивается на участки, в пределах которых функция внутренней силы не меняет своего аналитического выражения. За границы участков принимаются сечения, в которых приложены внешние нагрузки: сосредоточенные силы, сосредоточенные моменты, начинается или заканчивается распределенная нагрузка одного направления и изменяющаяся по одному закону, а также начало и конец балки.

Последовательно на каждом участке вводится скользящая система координатных осей (начало координат совмещается с началом участка) и для произвольного сечения составляются выражения для определения поперечной силы и изгибающего момента. Затем по этим выражениям в пределах каждого участка строятся графики (эпюры) внутренних сил.

Перед тем, как определять внутренние усилия (поперечные силы и изгибающие моменты) и строить эпюры, как правило, надо найти опорные реакции, возникающие в закреплении стержня. Если опорные реакции и внутренние усилия можно найти из уравнений статики, то конструкция называется статически определимой. Чаще всего мы встречаемся с тремя видами опорных закреплений стержней: жестким защемлением (заделкой), шарнирно-неподвижной опорой и шарнирно-подвижной опорой. На рис. 6.5 показаны эти закрепления. Для неподвижной (рис 6.5,б) и подвижной (рис. 6.5,в) опор приведены два эквивалентных обозначения этих закреплений. Напомним, что при действии нагрузки в одной плоскости в заделке возникают три опорных реакции (вертикальная, горизонтальная реакции и сосредоточенный реактивный момент) (рис. 6.5,а); в шарнирно-неподвижной опоре – две реактивные силы (рис. 6.3,б); в шарнирно-подвижной опоре – одна реакция – сила, перпендикулярная плоскости опирания (рис.6.5,в).

Рис. 6.5. Опорные реакции: а – в заделке; б – в шарнирно-неподвижной опоре;

в – в шарнирно-подвижной опоре

После определения опорных реакций внутренние усилия в статически определимых конструкциях определяем с помощью метода сечений.

Как было сказано выше, при плоском поперечном изгибе в балке возникают два внутренних усилия: поперечная сила Q и изгибающий момент M. В соответствии с методом сечений поперечную силу можно найти как сумму проекций всех внешних сил, взятых с одной стороны от сечения, на ось, перпендикулярную оси стержня (ось z). Изгибающий момент равен сумме моментов всех внешних сил, взятых с одной стороны от сечения, относительно оси, проходящей через центр тяжести рассматриваемого сечения (оси y).

Для того чтобы можно было вести расчет с любого конца балки, необходимо принять правило знаков для внутренних силовых факторов.

а)                                                                                                                     б)

Рис.6.7. а - правило знаков для поперечной силы Q; б - правило знаков для изгибающего момента M.

 

Если внешняя сила вращает отрезанную часть балки по часовой стрелке, то сила является положительной, если внешняя сила вращает отрезанную часть балки против хода часовой стрелки, то сила является отрицательной.

Если под действием внешней силы изогнутая ось балки принимает вид вогнутой чаши, такой, что идущий сверху дождь будет наполнять ее водой, то изгибающий момент является положительным. Если под действием внешней силы изогнутая ось балки принимает вид выпуклой чаши, такой, что идущий сверху дождь не будет наполнять ее водой, то изгибающий момент является отрицательным.

Достаточно очевидно и подтверждается опытом, что балка при изгибе деформируется таким образом, что волокна, расположенные в выпуклой части, растягиваются, а в вогнутой – сжимаются. Между ними лежит слой волокон, который лишь искривляется, не изменяя своей первоначальной длины (рис.6.8). Этот слой называется нейтральным или нулевым, а его след на плоскости поперечного сечения – нейтральной (нулевой) линией или осью.

Рис.6.8

 

При построении эпюр Q и М договоримся на эпюре Q положительные значения откладывать сверху нулевой линии. На эпюре М у строителей принято откладывать положительные ординаты снизу. Такое правило построения эпюры М называется построением эпюры со стороны растянутых волокон, т. е. положительные значения М откладываются в сторону выпуклости изогнутой балки.

Рассмотрим для простоты балку с прямоугольным поперечным сечением (рис.6.9). Следуя методу сечений, мысленно проведем разрез и отбросим какую-либо часть балки, а другую оставим. На оставшейся части покажем действующие на нее силы и в поперечном сечении – внутренние силовые факторы, которые являются результатом приведения к центру сечения сил, действующих на отброшенную часть. Учитывая, что внешние силы и распределенные нагрузки лежат в одной плоскости и действуют перпендикулярно оси балки, в сечении получим поперечную силу Q_y и изгибающий момент M_x. Эти внутренние силовые факторы заранее неизвестны, поэтому их показывают в положительном направлении в соответствии с принятыми правилами знаков.

Дифференциальные зависимости при изгибе

Правила проверки правильности построения эпюр

Для проверки эпюр используются следующие правила.

Эпюры N и T

В том сечении, где приложена сила (момент) на эпюре N (T) должен быть скачек на величину этой силы (момента). Скачком на эпюре называется разрыв первого рода (конечный разрыв).

Эпюра Q

1. В том сечении, где приложена сила, на эпюре должен быть скачек на величину этой силы. При движении по эпюре слева направо направления скачка должно совпадать с направлением силы.

2. Если участок не нагружен распределенной нагрузкой, то эпюра является прямой горизонтальной линией. При действии на участке распределенной нагрузки эпюра представляет собой прямую наклонную линию.

3. Если q < 0 (нагрузка направлена вниз), то поперечная сила слева направо уменьшается. При q > 0 (нагрузка направлена вверх) поперечная сила слева направо увеличивается.

Эпюра М

1. В том сечении, где приложен момент, на эпюре должен быть скачек на величину этого момента. При движении по эпюре слева направо при действии момента против хода часовой стрелки скачек должен быть направлен вниз, а при действии момента по ходу часовой стрелки – вверх.

2. Если участок не нагружен распределенной нагрузкой, то эпюра является прямой линией. При нагружении участка распределенной нагрузки эпюра представляет собой параболу. Парабола должна быть выгнута навстречу распределенной нагрузке.

3. При Q < 0 изгибающий момент слева направо уменьшается. Если Q > 0, то изгибающий момент слева направо увеличивается.

4. В том сечении, где Q = 0, на эпюре должна быть точка экстремума. При q < 0 (нагрузка направлена вниз) на эпюре расположена точка максимума, а при q > 0 (нагрузка направлена вверх) – точка минимума.

Понятие о напряженном состоянии в точке. Полное, нормальное и касательное напряжения

Напряженным состоянием в точке называется совокупность напряжений, действующих на всех возможных площадках, которые можно провести через эту точку.

Рассмотрим тело произвольной формы, нагруженное самоуравновешенной системой сил  .

Попробуем охарактеризовать напряженное состояние в произвольной точке тела С. С этой целью, выделим в окрестностях этой точки элементарный объём в виде куба с бесконечно малыми гранями. На каждой грани куба действуют внутренние силы, которые представим в виде трех составляющих вектора полного напряжения:

На невидимых гранях куба действуют такие же по величине, но противоположные по направлению напряжения. Полученные девять напряжений, называемых компонентами напряженного состояния, образуют так называемый тензор напряжений:

,

в котором, в соответствии с законом парности касательных напряжений:

+Таким образом, напряженное состояние в точке в общем случае нагружения может быть охарактеризовано шестью компонентами напряжений: тремя нормальными и тремя касательными.

Интегральная связь между напряжениями и внутренними силовыми факторами

Совокупность напряжений и , действующих по различным

площадкам в одной точке, представляет собой напряжённое состояние в этой точке.

Связь напряжений с внутренними силовыми факторами может быть описана следующими

соотношениями

где A - площадь сечения; x, y- текущие координаты элементарной площадки.

Условие прочности, задаваемое ограничением возникающих в сечении максимально

допускаемых значений напряжений, записывается в виде неравенства

где , - максимально допускаемые значения нормальных или касательных напряжений,

определяемые материалом изделия, его термообработкой, другими влияющими на прочность

технологическими факторами.

Понятие о деформированном состоянии в точке

Деформированным состоянием в точке называется совокупность деформаций, возникающих в различных направлениях и различных плоскостях, проходящих через данную точку.

Рассмотрим элементарный объем, находящийся в условиях объемного напряженного состояния.

Под действием напряжений этот объем деформируется, в результате каждая грань изменяет свои размеры в направлении координатных осей и может получить угловую деформацию. Так, например, передняя грань принимает вид:

Таким образом, в направлении оси z элементарный размер dz грани получит относительную деформацию  , а в направлении осиx элементарный размер dx изменится на величину  . Угол между ребрами грани изменится на величину .

Подобные деформации получат и остальные грани элементарного объема. Тогда деформированное состояние в точке определится тензором деформаций:

,

где линейные деформации

, ,

и угловые деформации

, , .

+Свойства деформированного состояния аналогичны свойствам напряженного состояния, в частности, можно выделить три взаимно перпендикулярные оси, в системе которых угловые деформации отсутствуют. Линейные деформации, возникающие в этой системе координат, называются главными деформациями. Главные деформации нумеруют в порядке убывания .

Различают линейное, плоское и объемное деформированные состояния.

линейное плоское объемное

Площадки главных напряжений и главных деформаций для линейно-упругого изотропного тела совпадают.

Линейные и угловые деформации

Линейная деформация - характеризует изменение размеров тела. Различают абсолютную деформацию ΔL и относительную деформацию ε = ΔL/L.

Угловая деформация - характеризует изменение формы тела и чаще всего называется углом сдвига

3. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ. Растяжение и сжатие прямолинейного стержня. Напряжения в поперечных сечениях. Деформации при растяжении-сжатии. Коэффициент Пуассона. Закон Гука. Модуль упругости. Потенциальная энергия деформации. Испытание материалов на растяжение-сжатие. Диаграммы на растяжение-сжатие различных материалов. Механические характеристики материалов. Пластичные и хрупкие материалы. Допускаемые напряжения, коэффициент запаса прочности. Условие прочности при растяжении-сжатии.

http://mysopromat.ru/uchebnye_kursy/sopromat/rastyazhenie_szhatie/

http://cdo.bru.by/course/distan/PGS/sopromat_pgsdz/Fail/lekcher_3.pdf

Деформация– изменение формы и размеров тела под действием приложенных сил.

Растяжение и сжатие прямолинейного стержня

Осевым растяжением (сжатием) стержня называется вид нагружения, при котором в поперечных сечениях стержня возникает только продольная сила N .

Величины внутренних сил находят с использованием метода сечений и принятого правила знаков.

Продольная сила N считается положительной, если она растягивает отсеченную часть стержня (рис. 2.1), т.е. направлена по направлению внешней нормали к сечению.

Графики, показывающие, как изменяются внутренние силы в направлении продольной оси стержня, называются эпюрами внутренних сил.

Напряжения в поперечных сечениях

Гипотеза плоских сечений(Д.Бернулли):

Поперечные сечения стержня, плоские до деформации, остаются плоскими и после деформации. Так как продольные слои стержня деформируются одинаково, то и нормальные напряжения во всех точках поперечного сечения должны быть одинаковыми. Поэтому в любом поперечном сечении   const , получаем

С ледовательно

 - равнодействующей напряжений. N - продольная сила, которая возникает в поперечных сечениях стержня.

Деформации при растяжении и сжатии

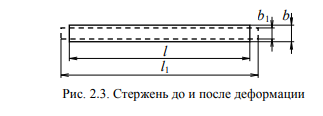Обозначим длину стержня через l, а высоту и ширину поперечного сечения b и a . На рис. 2.3 пунктирной линией показан стержень после растяжения.

Как показывают опыты, при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются. Его длина станет равной l1 , высота и ширина сечения – b1 и a1 . При сжатии – наоборот, стержень становится короче, а поперечные размеры увеличиваются.

При растяжении стержня продольная деформация вычисляется по формуле:

Относительные поперечные деформации в направлении сторон с размерами b и a:

……………………………………………………………………………………………..