
ответы / sm3
.docx3. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ
Растяжение и сжатие прямолинейного стержня.
Осевым растяжением (сжатием) стержня называется вид нагружения, при котором в поперечных сечениях стержня возникает только продольная сила N .
Величины внутренних сил находят с использованием метода сечений и принятого правила знаков.
Продольная сила N считается положительной, если она растягивает отсеченную часть стержня (рис. 2.1), т.е. направлена по направлению внешней нормали к сечению.
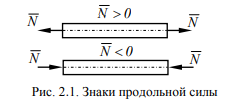
Графики, показывающие, как изменяются внутренние силы в направлении продольной оси стержня, называются эпюрами внутренних сил.
Напряжения в поперечных сечениях.
Гипотеза плоских сечений(Д.Бернулли):
П![]()
![]() оперечные
сечения стержня, плоские до деформации,
остаются плоскими и после деформации.
Так как продольные слои стержня
деформируются одинаково, то и нормальные
напряжения во всех точках поперечного
сечения должны быть одинаковыми. Поэтому
в любом поперечном сечении
const , получаем
оперечные
сечения стержня, плоские до деформации,
остаются плоскими и после деформации.
Так как продольные слои стержня
деформируются одинаково, то и нормальные
напряжения во всех точках поперечного
сечения должны быть одинаковыми. Поэтому
в любом поперечном сечении
const , получаем
Следовательно
- равнодействующей напряжений. N - продольная сила, которая возникает в поперечных сечениях стержня.
Деформации при растяжении и сжатии.
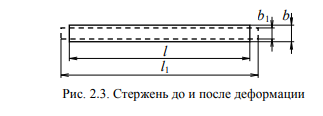 Обозначим
длину стержня через l, а высоту и ширину
поперечного сечения b и a . На рис. 2.3
пунктирной линией показан стержень
после растяжения.
Обозначим
длину стержня через l, а высоту и ширину
поперечного сечения b и a . На рис. 2.3
пунктирной линией показан стержень
после растяжения.
Как показывают опыты, при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются. Его длина станет равной l1 , высота и ширина сечения – b1 и a1 . При сжатии – наоборот, стержень становится короче, а поперечные размеры увеличиваются.
При растяжении стержня продольная деформация вычисляется по формуле:
![]()
Относительные поперечные деформации в направлении сторон с размерами b и a:
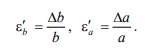
Коэффициент Пуассона.
Отношение относительной поперечной деформации к относительной продольной деформации , взятое по модулю, называется коэффициентом Пуассона:
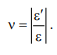
Величина является постоянной для изотропного материала и определяется экспериментально. Значения для различных материалов изменяются в пределах 0 0,5
З![]() акон
Гука.
акон
Гука.
В пределах малых деформаций для многих материалов справедлив закон Гука:
Нормальные напряжения в поперечном сечении прямо пропорциональны относительной продольной деформации
Коэффициент пропорциональности E в формуле (2.4) называется модулем упругости (модулем Юнга). Величина Е определяется экспериментально и является постоянной для изотропного материала.
Модуль упругости характеризует жесткость материала, т.е. способность сопротивляться деформированию.
Модуль упругости E и коэффициент Пуассона являются основными характеристиками упругости изотропного материриала.
Испытание материалов на растяжение-сжатие.
 Некоторые
свойства материалов проявляются при
испытаниях образцов из этих материалов
на растяжение. На основе этих экспериментов
определяются механические характеристики
материалов, позволяющие оценить их
прочностные и пластические свойства.
Некоторые
свойства материалов проявляются при
испытаниях образцов из этих материалов
на растяжение. На основе этих экспериментов
определяются механические характеристики
материалов, позволяющие оценить их
прочностные и пластические свойства.
 Для
проведения опытов на растяжение
используют специально изготовленные
образцы (рис. 2.5), которые закрепляются
в захватах машины и растягиваются вплоть
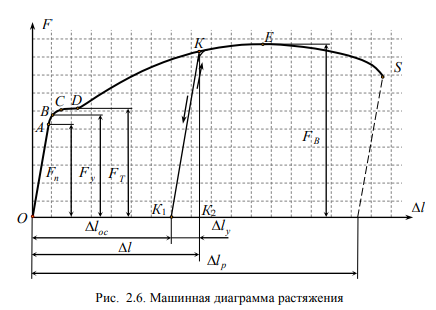
до разрушения. При этом зависимость
между растягивающей силой F и удлинением
образца l записывается
в виде графика (рис. 2.6), который называется
машинной диаграммой растяжения материала.
Для
проведения опытов на растяжение
используют специально изготовленные
образцы (рис. 2.5), которые закрепляются
в захватах машины и растягиваются вплоть
до разрушения. При этом зависимость
между растягивающей силой F и удлинением
образца l записывается
в виде графика (рис. 2.6), который называется
машинной диаграммой растяжения материала.
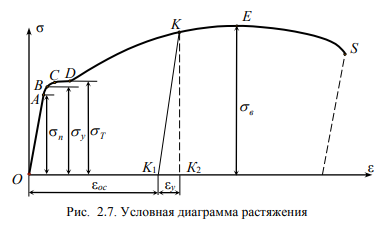
Рассмотрим диаграмму растяжения образца из малоуглеродистой стали (рис. 2.7). На этой диаграмме отмечены точки А, В, С, D.
Т![]() очке
А соответствует напряжение п
– предел пропорциональности. Пределом
пропорциональности называется наибольшее
напряжение, при котором деформация в
материале прямо пропорциональна
нагрузке:
очке
А соответствует напряжение п
– предел пропорциональности. Пределом
пропорциональности называется наибольшее
напряжение, при котором деформация в
материале прямо пропорциональна
нагрузке:
В![]() близи
точки А, на криволинейном участке
диаграммы, можно отметить точку В,
соответствующую пределу упругости у
. Пределом упругости называется наибольшее
напряжение, при котором в материале
возникает только упругая деформация:
близи
точки А, на криволинейном участке
диаграммы, можно отметить точку В,
соответствующую пределу упругости у
. Пределом упругости называется наибольшее
напряжение, при котором в материале
возникает только упругая деформация:
Н![]() ачиная
от точки С, диаграмма имеет горизонтальный
(или почти горизонтальный) участок,
которому соответствует предел текучести
т
. На этом участке деформации растут без
увеличения нагрузки. Пределом текучести
называется напряжение, при котором
деформация возрастает без заметного
увеличения нагрузки:
ачиная
от точки С, диаграмма имеет горизонтальный
(или почти горизонтальный) участок,
которому соответствует предел текучести
т
. На этом участке деформации растут без
увеличения нагрузки. Пределом текучести
называется напряжение, при котором
деформация возрастает без заметного
увеличения нагрузки:
![]() Горизонтальный
участок диаграммы CD называют площадкой
текучести. Площадка текучести ярко
выражена только для малоуглеродистых
сталей. Ее возникновение связано с
явлением текучести в материале. Точке
Е на диаграмме соответствует напряжение
в
– предел прочности. Пределом прочности
называется максимальное напряжение,
при котором образец не разрушается:
Горизонтальный
участок диаграммы CD называют площадкой
текучести. Площадка текучести ярко
выражена только для малоуглеродистых
сталей. Ее возникновение связано с
явлением текучести в материале. Точке
Е на диаграмме соответствует напряжение
в
– предел прочности. Пределом прочности
называется максимальное напряжение,
при котором образец не разрушается:
До достижения предела прочности в продольные и поперечные деформации образца равномерно распределяются по его длине.
После достижения точки Е диаграммы, образец в основном деформируется в окрестности одного наиболее ослабленного сечения, где начинает образовываться шейка – значительное сужение образца. Образец до деформации и после образования шейки показан на рис. 2.8.
За точкой
Е нагрузка снижается, что объясняется
уменьшением поперечного сечения шейки.
Разрыву образца на диаграмме соответствует
точка S.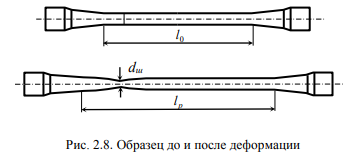
К прочностным характеристикам материала относятся предел пропорциональности п , предел упругости у , предел текучести т , предел прочности в (временный предел прочности).
Пластичность материала характеризуется относительным остаточным удлинением при разрыве и относительным остаточным поперечным сужением при разрыве .
В зависимости от величин δ и , конструкционные материалы условно делятся на пластичные и хрупкие. Материал считается пластичным, если относительная остаточная деформация больше 5 %.
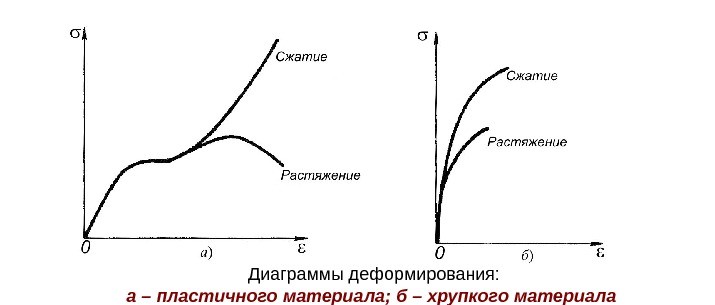
Хрупкие материалы разрушаются без образования заметных остаточных деформаций. К ним относятся чугун, стекло, кирпич, строительные камни. Величина удлинения δ при разрыве не превышает 2… 5%.
Пластичные материалы при нагружении способны образовывать большие остаточные деформации. К ним относятся медь, латунь, алюминий.
Испытание материалов на сжатие.
 Испытание
металлов на сжатие проводят на коротких
цилиндрических образцах.
Испытание
металлов на сжатие проводят на коротких
цилиндрических образцах.
На рис. 2.10 в первой четверти изображены диаграммы растяжения, а в третьей – сжатия. На начальном этапе нагружения диаграмма сжатия малоуглеродистой пластической стали Ст3, так же, как и диаграмма растяжения - наклонная прямая. Затем диаграмма переходит в криволинейный участок – участок текучести. При сжатии площадка текучести не получается такой же ярко выраженной, как при растяжении. Пределы пропорциональности, упругости и текучести для стали при сжатии такие же, как при растяжении. Углы наклона прямолинейных участков диаграммы (рис. 2.10) при растяжении и при сжатии одинаковы, значит, модуль упругости при сжатии такой же, как и при растяжении.
Условие прочности при растяжении-сжатии.
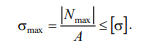 Условие
прочности имеет вид:
Условие
прочности имеет вид:
З![]() десь
– допускаемое
напряжение, величина которого вычисляется
по формуле:
десь
– допускаемое
напряжение, величина которого вычисляется
по формуле:
где о – опасное (предельное) напряжение, определяемое экспериментально; n – коэффициент запаса прочности. Значение коэффициента n зависит от предназначения конструкции и условий ее эксплуатации.
Для пластичных материалов за предельное (опасное) напряжение о обычно принимается предел текучести т. Для хрупких, а в некоторых случаях и для умеренно пластичных материалов за о принимается предел прочности в.
Величина коэффициента запаса прочности n назначается с учетом многих факторов: используемая для расчетов теория, условия эксплуатации конструкции, наличие требований по безопасности объекта, принятые в отрасли промышленности.
Во многих случаях n = 1,4 3. Например, при проектировании машин и аппаратов химических производств, в ряде случаев полагают n = 1,5.
Потенциальная энергия деформации.
П![]() отенциальная
энергия деформации – это энергия,
накопленная в теле при его деформировании
под действием внешних сил.
отенциальная
энергия деформации – это энергия,
накопленная в теле при его деформировании
под действием внешних сил.
П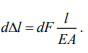 о
закону Гука, при действии на стержень
продольной силы F, возникает удлинение
о
закону Гука, при действии на стержень
продольной силы F, возникает удлинение
И![]() зменение
силы на величину dF приводит к изменению
удлинения на величину
зменение
силы на величину dF приводит к изменению
удлинения на величину
При этом совершается элементарная работа
![]() Суммируя
элементарные работы, которые совершает
сила при изменении от 0 до N, получаем
Суммируя
элементарные работы, которые совершает
сила при изменении от 0 до N, получаем
П![]() о
закону сохранения энергии, работа
продольной силы W равна потенциальной
энергии деформации Uо : W Uо.
о
закону сохранения энергии, работа
продольной силы W равна потенциальной
энергии деформации Uо : W Uо.
Следовательно,
Удельной потенциальной энергией деформации U называется величина потенциальной энергии деформации, накопленной в единице объема тела.
