ответы / Лекция-59-Т-282гр.-3-пара

Лекция 59

Тема: Дифференциальные зависимости при изгибе

Между изгибающим моментом, поперечной силой и интенсивностью распределённой нагрузки существуют дифференциальные зависимости, основанные на теореме Журавского, названой по имени замечательного русского инженера-мостостроителья Д.И. Журавского(1821-1891) которая формулируется следующим образом: поперечная сила равна первой производной от изгибающего момента по абсциссе сечения балки.

Для доказательства рассмотрим балку, показанную на рис. 65. Начало координат возьмём на левом конце балки, а ось Z направим вправо.

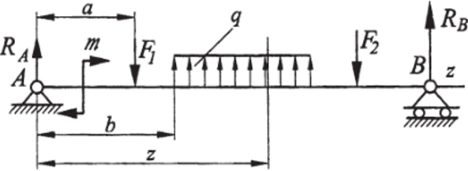
Рис. 65. К выводу дифференциальной зависимости между поперечной силой и изгибающим моментом (теорема Журавского)

Проведём сечение на одном из участков балки с текущей координатой 1 и запишем уравнение изгибающего момента:

Дифференцируя это выражение 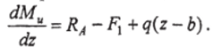 по координате г, получим

Выражение, стоящее в правой части, есть поперечная сила Q в сечении z. Следовательно, что и требовалось доказать.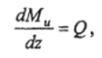 

Продифференцировав уравнение изгибающего момента еще раз, получим 

то есть вторая производная от изгибающего момента или первая производная от поперечной силы по абсциссе сечения балки равна интенсивности распределенной нагрузки.

Из высшей математики известно, что по знаку второй производной можно судить о выпуклости или вогнутости кривой. Это правило можно использовать при построении эпюр. Если q > 0, то эпюра М_и будет расположена выпуклостью вниз, а если q < 0 - то выпуклостью вверх.

Эпюры поперечных сил и изгибающих моментов, кроме наглядного изображения распределения их вдоль оси балки, дают возможность определить опасное сечение балки и установить значения поперечной силы и изгибающего момента в данном сечении. Эпюры поперечных сил и изгибающих моментов можно строить двумя способами.

Правила контроля эпюр с помощью диф. зависимостей;

1)если на участке балки отсутствует распределенная нагрузка, то эпюра Q-прямая параллельная оси эпюры. Эпюра моментов здесь – наклонная прямая.

2)если на участке имеется распределенная нагрузка, то эпюра Q-наклонная прямая, а М-парабола.

3) если на некотором участке;

А) Q>0, то М возрастает слева на право

б) Q=0, то М параллельно оси эпюры

в) Q <0, то М убывает слева на право

4)в точке, где эпюра Q пересекает ось х, эпюра М имеем экстремум.

5)под сосредоточенной внешней силой на эпюре Q наблюдается скачек ординаты (если сила +, то скачек вверх; –, то скачек вниз), а на эпюре М-излом, острие которого направлено на встречу действия силы

6)в начале и конце участка с распределенной нагрузкой параболические и прямолинейные части эпюры М сопрягаются плавно(если нет приложенных там сосредоточенных сил)

7)если q направлена вниз (q<0),парабола М направлена вверх (то есть навстречу q) и наоборот-q<0-выпуклость вниз

8)в сечении на свободном или шарнирно опертом конце балки М=0(если нет сосредоточенного момента), если есть сосредоточенный момент то равна этому моменту

9)под внешним моментом М на эпюре М наблюдается скачек на величину этого момента. На эпюре Q это не отражается. Если внешний момент сжимает верхние слои то скачек вверх, если сжимает нижние, то скачек вниз.

10)в сечении, совпадающим с заделкой, изгибающий момент и перерезывающая сила численно равны реактивному моменту и опорной реакции.

Дифференциальные зависимости при изгибе;

-первая диф. зависимость: q=dQ(x)/dx. Первая производная от перерезывающей силы по длине балки равна погонной нагрузке

-вторая диф. зависимость: Q(x)=dM(x)/dx. Величина Q(х)=-а tg угла наклона на эпюры М ( касательной эпюры) к оси эпюры

-третья диф. зависимость q=d² M(x)/dx²

Когда на рассматриваемом участке действует, кроме того, распределённый момент интенсивностью m, H·м/м, формула принимает следующий вид;

dM/dx=Q+m

Контрольные вопросы:

1.Какие внутренние силовые факторы возникают при : чистом изгибе, поперечном изгибе?

2.Кто установил зависимости между изгибающим моментом, поперечной силой и интенсивностью распределённой нагрузки?

3.Как формулируется теорема Журавского?

4.Чему равна поперечная сила по длине балки(формула)?

5. Чему равна интенсивность равномерно распределенной нагрузки(формула)?

Литература: Сопротивление материалов А.А.Эрдеди стр.