Расчеты на прочность при изгибе.

1. При проверочном расчете определяется максимальное расчетное напряжение, которое сравнивается с допускаемым напряжением:

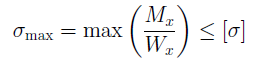
2. При проектном расчете подбор сечения бруса производится из условия:

3. При определении допускаемой нагрузки допускаемый изгибающий момент определяется из условия:

Далее по полученному значению [M_x] определяют допускаемые значения внешних поперечных нагрузок [Q] и внешних изгибающих моментов [M_внеш]. Условие прочности имеет вид:

11111111111111111111111111111111111111111111111111111111111111

Условие прочности при изгибе формулируется следующим образом: максимальное значение нормального напряжения в балке не должно превышать допускаемого напряжения. Следовательно, с учетом формулы для вычисления максимального нормального напряжения

должно выполняться условие прочности

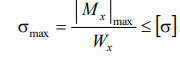
Для хрупких материалов, у которых прочность при сжатии выше, чем при растяжении, допускаемые напряжения на растяжение с  р . Поэтому для хрупких материалов используются два условия прочности:

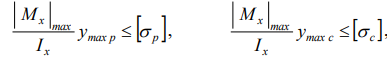
Наряду с условием прочности (1) при расчете на прочность следует проверять выполнение условие прочности по максимальным касательным напряжениям :

Дифференциальное уравнение изгиба балки и его интегрирование и его граничные условия

дифференциальное уравнение изгиба балки:

9. Сложное сопротивление

Сложным сопротивлением называются такие виды нагружения стержня, при которых в его поперечных сечениях одновременно возникает несколько внутренних силовых факторов.

Косой изгиб.

называется вид нагружения стержня, при котором плоскость действия изгибающего момента M не проходит через главную ось поперечного сечения

Определение напряжений и положения нейтральной линии.

Положение нейтральной линии можно определить с помощью формулы (2.1), если предположить, что точка  с координатами лежит на нейтральной линии. В этом случае нормальное напряжение в точке равно нулю

,

или

. (2.2)

Уравнение нейтральной линии при косом изгибе (2.2) есть уравнение прямой, проходящей через начало координат.

Положение нейтральной линии определяется тангенсом угла ее наклона  (рис.2.3) к главной оси . С учетом (2.2) находим

,

,  . (2.3)

Так как в общем случае  и, следовательно, , то можно заключить, что при косом изгибе нейтральная линия не перпендикулярна к линии действия внешней силы.

Из формулы (2.3) следует, что для сечений с  (квадрат, круг, кольцо, правильный многоугольник), т.е. для сечений, у которых любые центральные оси являются главными, углы и равны, и нейтральная линия перпендикулярна линии действия внешней силы. Балки такого сечения не испытывают деформации косого изгиба.

Определение положения нейтральной линии позволяет выявить опасные точки сечения. Для этого следует построить касательные к контуру сечения, параллельные нейтральной линии. Точки касания и будут являться опасными (точки  и на рис.2.3).

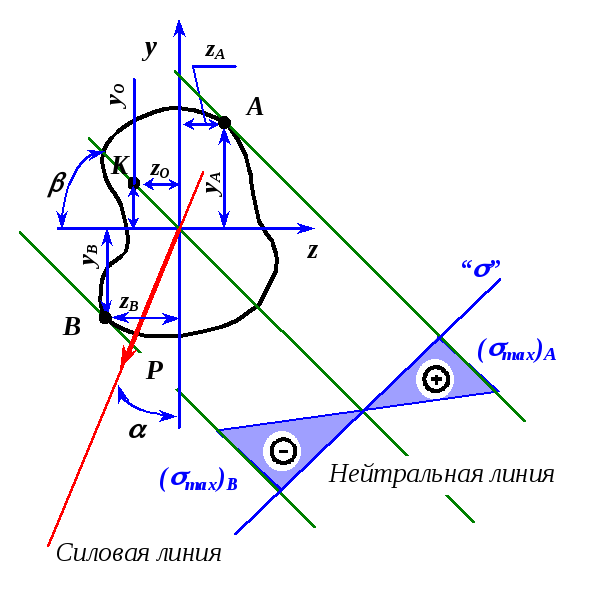
Рис. 2.3

Для некоторых сечений (прямоугольник, двутавр, швеллер и т.п.) наиболее напряженные точки расположены в углах этих сечений, т.е. их можно найти без определения положения нейтральной линии (рис.2.4).

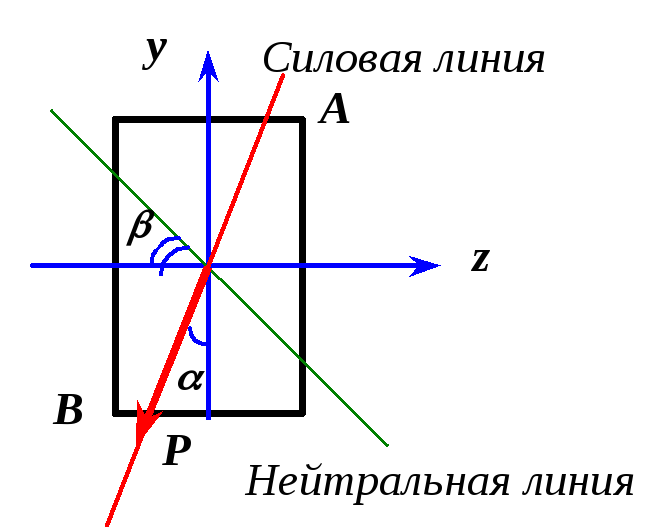
Рис. 2.4

Условия прочности составляют в зависимости от свойств того материала, из которого изготовлен элемент конструкции (брус).

Для хрупкого материала используют два условия прочности - для опасной точки, где имеет место растяжение (для нашего случая т.  на рис.2.3), и для точки, где имеет место сжатие (т. )

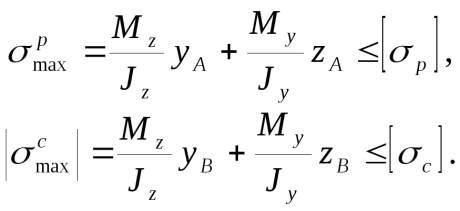 (2.4)

Необходимость использования двух условий прочности для хрупкого материала объясняется разными механическими свойствами материала при растяжении и сжатии. Хрупкий материал плохо сопротивляется растяжению и хорошо - сжатию.

Для пластичного материала, который одинаково сопротивляется и растяжению и сжатию, используют одно условие прочности для точки поперечного сечения, где имеют место максимальные по абсолютной величине нормальные напряжения

 (2.5)

где  и - координаты данной точки.

+При расчетах на прочность касательными напряжениями от поперечных сил пренебрегают, т.к. их влияние незначительно.

Определение напряжений при косом изгибе

Рассмотрим консольную балку, нагруженную сосредоточенной силой как показано на рис.2.2.

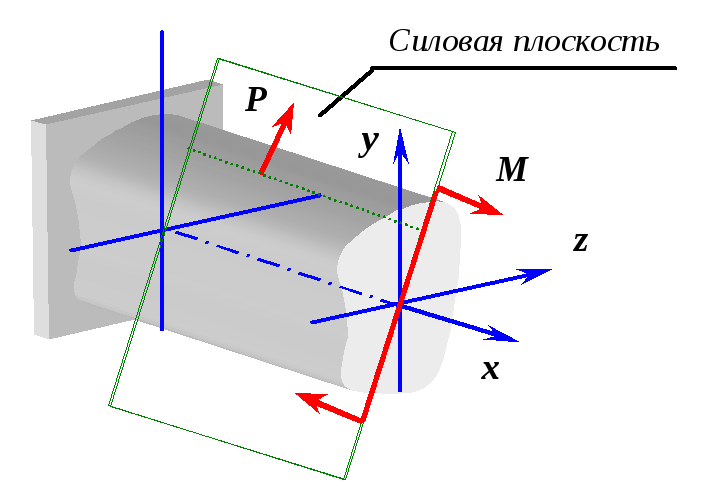
Рис. 2.1

Находим проекции силы  на главные центральные оси инерции и (рис.2.2):

и  .

Каждая из проекций располагается в одной из главных центральных плоскостей инерции и, таким образом, косой изгиб является сочетанием двух плоских поперечных изгибов и часто называется двойным.

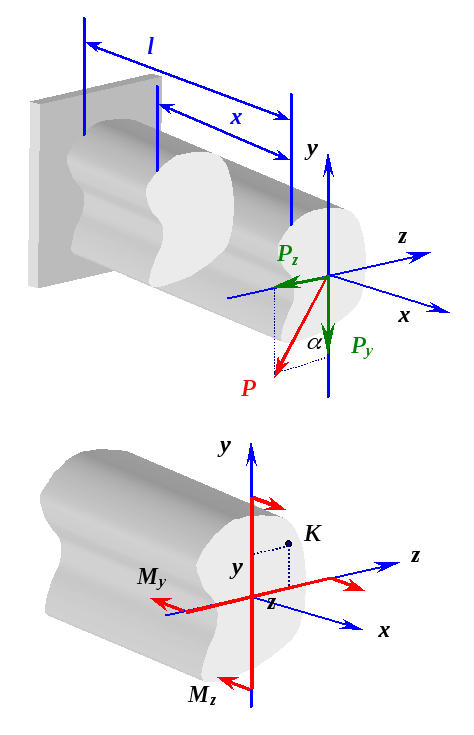
Рис. 2.2

В произвольном сечении на расстоянии  от точки приложения си­лы имеют место четыре внутренних силовых фактора:

поперечные силы:  ,

;

и изгибающие моменты:  ,

.

Определим напряжения, возникающие в произвольной точке  рассматриваемого сечения (рис.2.2):

от изгибающего момента 

,

от изгибающего момента 

,

здесь  и - координаты точки, в которой рассчитывают напряжения.

Знак напряжения зависит от характера деформации (растяжение-плюс, сжатие-минус). В нашем случае оба напряжения являются растягивающими и имеют знак плюс.

На основании ПНДС полное нормальное напряжение в точке  равно их алгебраической сумме:

. (2.1)

+При проведении расчетов на прочность условие прочности составля­ется для опасной точки поперечного сечения, т.е. для точки, в которой нормальные напряжения достигают максимальных значений. Самой нагруженной точкой в сечении произвольной формы является точка, наиболее удаленная от нейтральной линии, разделяющей растянутую и сжатую зоны сечения.

В связи с этим, большое значение приобретают вопросы, связанные с определением положения нейтральной линии.

Расчет на прочность. Изгиб с кручением.

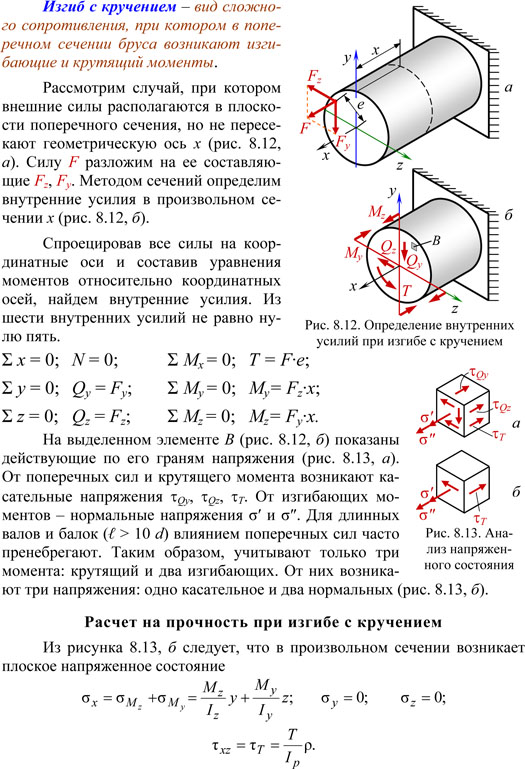
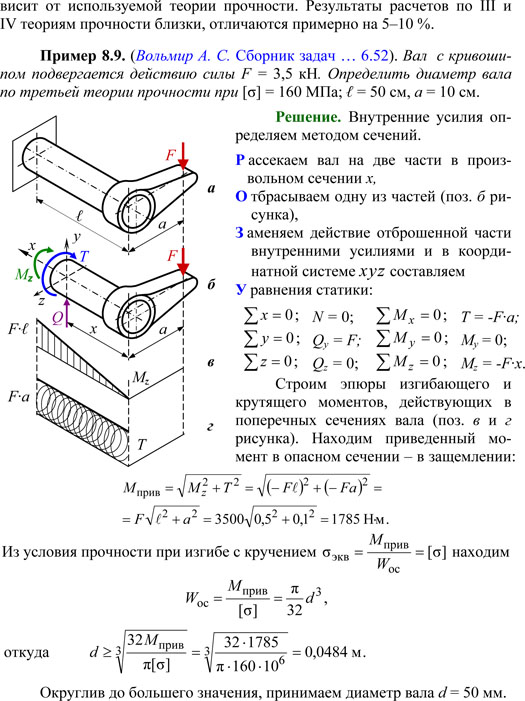
Внецентренное действие продольной силы.

Внецентренным нагружением называют случай, когда продольная сжимающая либо растягивающая сила приложена не к центру тяжести сечения, а с некоторым смещением от него, называемым эксцентриситетом