ПРОГРАММА

по дисциплине “Сопротивление материалов”

(ФЭМТО , 2021 г.)

1. ВВЕДЕНИЕ

Курс сопротивления материалов. Прочность, жесткость и

устойчивость элементов конструкций. Основные гипотезы, принимаемые в курсе сопротивления материалов.

Реальный объект и расчетная схема. Схематизация элементов конструкций (стержень, пластина, оболочка, массивное

тело). Виды внешних сил. Объемные и поверхностные нагрузки.

Виды опор. Опорные реакции. Уравнения статики.

2. ВНУТРЕННИЕ СИЛЫ

Метод сечений. Внутренние силовые факторы в поперечном сечении стержней. Продольная сила. Построение эпюр

продольных сил. Крутящий момент. Построение эпюр крутящих

моментов. Плоский изгиб. Построение эпюр изгибающего момента и поперечной силы. Дифференциальные зависимости

при изгибе. Правила проверки правильности построения эпюр.

Понятие о напряженном состоянии в точке. Полное, нормальное и касательное напряжения. Интегральная связь между

напряжениями и внутренними силовыми факторами. Понятие о

деформированном состоянии в точке. Линейные и угловые деформации.

3. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ

Растяжение и сжатие прямолинейного стержня. сечении стержня возникают шесть внутренних силовых факторов: N – продольная сила, Qx , Qy – поперечные силы, T – крутящий момент, M x , M y – изгибающие моменты. В ряде случаев внешние силы действуют так, что некоторые из внутренних силовых факторов равны нулю. Осевое только N, Величины внутренних сил находят с использованием метода сечений и принятого правила знаков. Продольная сила N считается положительной, если она растягивает отсеченную часть стержня (рис. 2.1 ), т.е. направлена по направлению внешней нормали к сечению. Графики, показывающие, как изменяются внутренние силы в направлении продольной оси стержня, называются эпюрами внутренних сил.

Напряжения в поперечных сечениях. Деформации при растяжении и сжатии. Коэффициент Пуассона. Закон Гука. Модуль упругости.

Потенциальная энергия деформации.

6

Испытание материалов на растяжение-сжатие. Диаграммы

на растяжение-сжатие различных материалов. Механические

характеристики материалов. Пластичные и хрупкие материалы.

Допускаемые напряжения, коэффициент запаса прочности.

Условие прочности при растяжении-сжатии.

4. ГЕОМЕТРИЧЕСКИЕ ХАРАКТЕРИСТИКИ ПЛОСКИХ ФИГУР

Основные геометрические характеристики плоских фигур. при растяжении и сжатии стержней, возникающие в стержне напряжения и удлинение, определяются по формулам  и l влияет размер площади поперечного сечения стержня А и не оказывает влияния форма сечения Площадь поперечного сечения А является одной из геометрических характеристик поперечного сечения стержня. При других видах деформаций стержня на величины напряжений и перемещений существенное влияние оказывают как размеры, так и форма поперечного сечения стержня. если на заделанный одним концом стержень с поперечным сечением в виде вытянутого прямоугольника действует сила, приложенная на свободном конце стержня, то стержень будет изгибаться и его конец переместится на некоторую величину 1 v (рис. 4.1а). Если же стержень повернуть на угол 90 а) б)

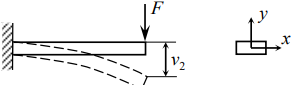
вокруг его продольной оси так, чтобы наибольшая сторона поперечного сечения располагалась горизонтально, то под действием той же вертикально направленной силы конец стержня переместится на величину 2 v (рис. 4.1б). Окажется, что v2  v1 при одной и той же площади поперечного сечения, стержень по–разному сопротивляется действию силы. Следовательно, площадь поперечного сечения стержня не может характеризовать сопротивляемость изгибу Статический момент инерции, определение центра тяжести фигуры. Статическими моментамии инерциии фигуры относительно осей Ох и Оу называются величины Sx и Sy, определяемые по формулам Можно показать, что координаты центра тяжести фигуры хс , ус вычисляется по формулам Осевой, полярный и центробежный моменты инерции фигур. Оси координат, проходящие через центр тяжести фигуры, называются центральными осями. Очевидно, что для центральных осей хс  ус  0. Из представленных здесь формул для вычисления с х , с у следует, что для центральных осей статические моменты инерции фигуры равны нулю ( Sx  Sy  0 )величины. называются осевыми моментами инерции фигуры относительно осей Ох и Оу, соответственно. Интеграл по площади фигуры называется полярным моментом инерции. Величина – центробежный момент инерции фигуры. Моменты инерции простейших фигур.

Изменения геометрических характеристик при параллельном переносе осей координат. Из рисунка видно, что для произвольной точки С фигуры x1  x b, y1  y  a . Вычислим момент инерции фигуры относительно оси О1х1 Если оси Ох, Оу являются центральными осями, то Sx  Sy  0 . В этом случае формулы (4.2), (4.3), определяющие связь между моментами инерции фигуры, вычисленными относительно осей О1х1, О1у1 и Ох, Оу, принимают вид: Изменения моментов инерции

при повороте осей координат. Найдем зависимость между моментами инерции относительно осей Ох, Оу и моментами инерции относительно осей Ох1, Оу1, повернутых на угол  Можно показать, что cos sin ; x1  x  y  cos sin . y1  y  x  Определим моменты инерции фигуры относительно осей Ох1 и Оу1 Аналогично определяются 1 y I , 1 1 x y I . В результате получаются формулы, определяющие зависимость между моментами инерции относительно осей Ох, Оу и моментами инерции относительно осей Ох1, Оу1, повернутых на угол  : Складывая левые и правые части первых двух урав Следовательно, Получилось, что сумма моментов инерции относительно любых взаимно перпендикулярных осей остается постоянной и не изменяется при повороте системы координат.

Главные оси и главные моменты

инерции. существует такое значение угла поворота осей   0 , при котором величины осевых моментов инерции достигают экстремальных значений. Это значит, что осевой момент инерции относительно одной из осей достигает своего максимального значения, а относительно другой оси момент инерции принимает минимальное значение. Экстремальные значения осевых моментов инерции называются главными моментами инерции. 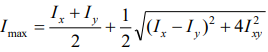Значения этих величин определяются по формулам: Для нахождения значения 0 используем условие экстремума Положив в этом уравнении   0 , находим (I y  I x )sin20 2I xy cos20  0 Из этого уравнения следует, что Оси, относительно которых осевые моменты инерции принимают экстремальные значения, называются главными осями. Главные оси фигуры взаимно перпендикулярны. Главные оси, проходящие через центр тяжести фигуры, называются главными центральными осями. Если фигура имеет ось симметрии, то эта ось является одной из главных центральных осей инерции фигуры

5. ОСНОВЫ ТЕОРИИ НАПРЯЖЕННОГОДЕФОРМИРОВАННОГО

СОСТОЯНИЯ

Напряженное состояние в точке. Компоненты напряжения.

Виды напряженных состояний. Плоское напряженное состояние.

Закон парности касательных напряжений. Напряжения на

наклонных площадках. Главные напряжения. Максимальные

касательные напряжения. Чистый сдвиг. В некоторых частных случаях нормальные напряжения на гранях параллелепипеда могут быть равны нулю. Напряженное состояние, при котором по граням параллелепипеда действуют только касательные напряжения, называется чистым сдвигом. Чистый сдвиг возникает при кручении стержней и при деформировании заклепочных соединений. на гранях которого действуют только касательные напряжения  Параллелепипед после деформации показан на рис. 3.9б штриховой линией. При условном совмещении нижних границ граней деформированного и недеформированного параллелепипеда, получается рисунок 3.9в.

Закон Гука при сдвиге. Величина γ называется относительным сдвигом (углом сдвига).

Экспериментально полученный график зависимости между касательным напряжением τ и углом сдвига  для пластичного материала показан на рис. 3.10. Очевидно, что этот график аналогичен диаграмме растяжения материала. Начальный участок диаграммы ОА – прямая линия. На этом участке зависимость между τ и  описывается законом Гука при сдвиге:   G  , (3.11) где G – модуль сдвига, который характеризует жесткость материала при сдвиге. Величина модуля сдвига G связана с модулем упругости Е и коэффициентом Пуассона ν соотношением G  (3.12) Можно показать, что удельная потенциальная энергия деформации при чистом сдвиге вычисляется по формуле чистом сдвигеU  1/2

Деформированное состояние в точке. В любой точке тела можно выделить отрезки dx, dy, dz параллельные осям координат и определить перемещения u, v, w, линейные деформации  x,  y,  z, а также изменения углов между этими отрезками – угловые деформации  xy,  xz,  yz. Совокупность перемещений u, v, w, линейных  x,  y,  z и угловых  xy,  xz,  yz деформаций определяет деформированное состояние тела в точке. Компоненты деформации. Обобщенный закон Гука. Обобщенный закон Гука связь между напряжениями и деформациями в случае объемного напряженного состояния. может быть получен с использованием принципа независимости действия сил, на основании закона Гука при растяжении-сжатии стержня и при чистом сдвиге Как уже отмечалось, объемное напряженное состояние можно описать с использованием главных напряжений 1 , 2 , 3 . В этом случае, касательных напряжений на гранях параллелепипеда нет и возникают только линейные деформации  1, 2 , 3 . Используя принцип независимости действия сил и учитывая наличие продольных и поперечных деформаций, можно записать, что линейная деформация в направлении действия напряжения 1 1  11 12 13 , где 11 – деформация от действия напряжения 1 ; 12 – поперечная деформация в направлении 1 , вызванная действием напряжения 2 ; 13 – поперечная деформация от действия 3 . Как было показано, при растяжении стержня возникают продольная  и поперечная  деформации, которые вычисляются по формулам Аналогично выводятся формулы для деформаций 2 ,  3, возникающих в направлении действия напряжений 2 , 3 . В результате получается, что Соотношения обобщенного закона Гука могут быть записаны и для произвольно ориентированных площадок. В этом случае кроме линейных деформаций x y z  ,  ,  следует учитывать также и угловые деформации  xy,  yz,  xz, которые связаны с касательными напряжениями законом Гука при сдвиге:   G  . При этом получается, что обобщенный закон Гука содержит шесть уравнений, связывающих деформации и напряжения. При этом получается, что обобщенный закон Гука содержит шесть уравнений, связывающих деформации и напряжения

Потенциальная энергия при растяжении и сжатии удельная потенциальная энергия деформации полученный результат можно обобщить на случай объемного напряженного состояния. Для параллелепипеда образованного главными площадками, на гранях которого действуют главные напряжения 1 , 2 , 3 можно преобразовать с помощью формул обобщенного закона Гука При чистом сдвиге Поэтому в случае произвольно ориентированных площадок, с учетом касательных напряжений, Известно, что U Uф Uоб , где Uф – величина потенциальной энергии, связанная с изменением формы, Uоб – потенциальная энергия деформации, обусловленная изменением объема. Можно показать, что

деформации.

6. ТЕОРИИ ПРОЧНОСТИ

Основные понятия. Первая, вторая и третья теории прочности. Четвертая (энергетическая) теория прочности. Теория

прочности Мора.

7

7. КРУЧЕНИЕ

Кручение стержня с круглым поперечным сечением.

Определение напряжений и угла закручивания. Расчет валов на

прочность и жесткость.

8. ИЗГИБ

Плоский изгиб балок. Чистый изгиб. Нормальные напряжения при чистом изгибе. Касательные напряжения при изгибе.

Расчет балки на прочность.

Дифференциальное уравнение изгиба балки и его интегрирование. Граничные условия.

9. СЛОЖНОЕ СОПРОТИВЛЕНИЕ

Косой изгиб. Определение напряжений и положения

нейтральной линии. Расчет на прочность. Изгиб с кручением.

Внецентренное действие продольной силы.

10. УСТОЙЧИВОСТЬ СЖАТЫХ СТЕРЖНЕЙ

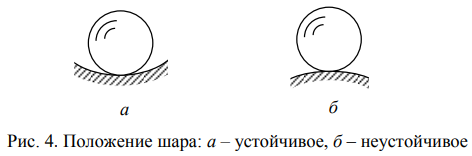
Основные понятия об устойчивости. Состояние системы называется устойчивым, если малые возмущающие силы не приводят к существенному изменению ее исходного положения. Состояние системы будет неустойчивым, если малые возмущения приводят к существенному изменению ее исходного положения. Явление потери устойчивости может возникать и для сжатого стержня. Если величина сжимающей силы F меньше некоторого значения Fкр, то стержень сохранит свое прямолинейное положение. В случае F  Fкр , стержень изогнется, потеряет устойчивость. Сила Fкр , при которой сжатый стержень теряет устойчивость, называется критической силой. Метод Эйлера для

определения критических сил. Определим величину Fкр для сжатого стержня с шарнирно закрепленными концами. После потери устойчивости стержень изогнется и займет положение, показанное на рис 5 штриховой линией. Изогнутое положение будет определяться прогибом v (z) , который должен удовлетворять дифференциальному уравнению изгиба балки Как видно из рисунка, величина изгибающего момента Рис. 5. Сжатый стержень при потере устойчивости в сечениях стержня M F v (z) x  кр и дифференциальное уравнение изгиба принимает вид: где Общее решение этого уравнения v z Ccoskz Dsinkz . (2) Здесь С и D – постоянные интегрирования, которые определяются из граничных условий называется формулой Эйлера. Она используется для определения критической силы, при которой стержень теряет устойчивость. Отметим, что в полученном выражении для прогиба v z  Dsinkz, величина постоянной D осталась неопределенной, Влияние условий закрепления на

величину критической силы. для других способах закрепления концов стержня е μ – коэффициент приведенной длины, зависящий от способа закрепления концов стержня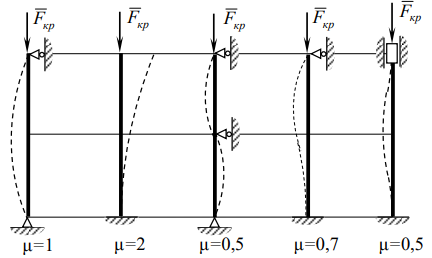 При выводе формулы Эйлера предполагалось, что потеря устойчивости стержня происходит в плоскости Оуz (рис. 5). Поэтому в формулы (3), (4) входит величина осевого момента инерции Ix. Потеря устойчивости стержня может произойти и в плоскости перпендикулярной к Оyz. В этом случае в формулы (3), (4) вместо Ix должна входить величина Iу. В общем случае потеря устойчивости стержня происходит в плоскости его наименьшей жесткости, следовательно, наименьшая критическая сила будет определена по формуле где min I – наименьшее из величин Ix и Iу .

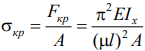
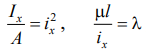
Пределы применимости формулы Эйлера. Формула Эйлера может быть использована, если возникающие в материале стержня напряжения σкр не превышают предела пропорциональности кр  п . Величина х i называется радиусом инерции сечения, λ – гибкостью стержня. Условие того, что критические напряжения не должны превышать предела пропорциональности Следовательно,    E п 2 2 . Чтобы выполнялось условие (6), значение гибкости стержня λ должно быть больше или равно предельному значению пред :   пред . значение пред зависит только от свойств материала. Расчет стержня

на устойчивость при растяжениях, превышающих предел пропорциональности. Если гибкость стержня меньше пред , то расчеты по формуле Эйлера получаются с большой погрешностью, т.к. при выводе формулы Эйлера предполагалось, что деформации являются упругими и справедлив закон Гука. В случаях, когда гибкость стержня   пред , при потере устойчивости в материале возникают пластические деформации. Формула Ясинского. В случаях, когда гибкость стержня   пред , при потере устойчивости в материале возникают пластические деформации. Расчет на устойчивость в этом случае выполняется с использованием формулы Ясинского: кр  a b . Здесь а и b – константы, определяемые для каждого материала экспериментально. Для коротких стержней, гибкость которых     (для металлических стержней   4050  ), потеря устойчивости не происходит. Такие стержни разрушаются без потери устойчивости, поэтому если гибкости     , то проводить расчет на устойчивость не требуется. Расчет стержней на

устойчивость с использованием коэффициента снижения допускаемых напряжений. Потеря устойчивости стержней происходит при напряжениях, величина которых меньше или равна напряжения при котором происходит потеря прочности. Поэтому, допускаемые напряжения [кр] при расчете на устойчивость должны быть меньше или равны допускаемых напряжений при расчете на прочность  . Следовательно, [ ]    кр , где  – коэффициент снижения допускаемых напряжений, величина которого зависит от материала и гибкости стержня и изменяется в пределах 0   1 При расчете на устойчивость с применением коэффициента φ используется условие  F/A   , ( 0   1 ). Зависимость  () достаточно сложная, так как она учитывает возможность разрушения стержня при сжатии (   * ), а так же потери устойчивости при упругих ( пред   ) и пластических (     пред * ) деформациях. Поэтому зависимость  () задается в виде 14 таблицы (табл. 1) и вычисления производятся методом последовательных приближений 1) Задается значение   1  0,5 и из условия (7) определяется площадь поперечного сечения стержня AF/ ( 1) 2) По найденной величине площади сечения А вычисляются размеры сечения, его геометрические характеристики и подсчитывается гибкость   l/ i х. 3) По найденному значению λ из таблицы находится значение ' 1 и вычисляется величина   |1  ’1|/ ’1 100%. 4) Если получается, что   5% , расчеты повторяют для нового значения   2  1 1 '/ 2

11. ЭНЕРГЕТИЧЕСКИЕ МЕТОДЫ

Потенциальная энергия деформации стержня. Теорема Кастильяно. Метод Мора.

13. КОНЦЕНТРАЦИЯ НАПРЯЖЕНИЙ.

Основные понятия. Примеры концентраторов напряжений.

Анализ распределений напряжений в простейших конструкциях

8

с концентратором напряжений. Теоретический коэффициент

концентрации напряжений. Способы снижения концентрации

напряжений.

14. РАСЧЕТ КОНСТРУКЦИЙ НА ВЫНОСЛИВОСТЬ

Понятие об усталостном разрушении. Виды циклов

напряжнений. Предел выносливости. Диаграмма предельных

амплитуд. Факторы, влияющие на величину предела выносливости.

1. Введение

Курс сопротивления материалов.

Сопротивление материалов является одним из разделов науки о прочности, в котором излагаются закономерности деформирования и разрушения тел, основанные на теоретических исследованиях и данных экспериментов.

Прочность, жесткость и устойчивость элементов конструкций.

Прочность – это свойство конструкции сопротивляться разрушению при действии на нее внешних сил (нагрузок).

Жесткость – свойство конструкции сопротивляться деформированию. Конструкция считается жесткой, если при действии внешних сил изменения ее размеров и формы сравнительно малы.

Устойчивость – свойство системы сохранять свое начальное равновесное положение при малых внешних воздействиях, не учитываемых в расчете.

Основные гипотезы, принимаемые в курсе сопротивления материалов.

Деформацией называется изменение взаимного расположения частиц тела, вызывающее изменение его размеров и формы. Если си-лы, вызывающие деформацию, постепенно уменьшать и затем полно-стью снять, то тело будет стремиться приобрести свою первоначаль-ную форму. Деформации полностью или частично исчезнут.

Свойство тел деформироваться под нагрузкой и затем после устранения сил восстанавливать свою первоначальную форму, назы-вается упругостью. Часть деформации, которая исчезает после снятия нагрузки, называется упругой деформацией, а та часть, которая остает-ся, называется остаточной деформацией. Возникновение остаточной деформации связано с так называемой пластичностью тела. Если де-формации после снятия нагрузки полностью исчезли, то тело называ-ют абсолютно упругим.

У некоторых материалов упругие свойства одинаковы во всех направлениях. Такие тела называются изотропными. Анизотропным называется тело, у которого упругие свойства различны в разных направлениях.

Если деформации являются упруги-ми, то используется принцип независимости действия сил (принцип суперпозиции). В соответствии с этим принципом – результат сов-местного действия нескольких сил равен сумме результатов от дей-ствия каждой из сил в отдельности.

Полагается, что возникающие в теле деформации и перемещения являются малыми. Кроме того, принимаются предположения, позво-ляющие значительно упростить расчеты:

 принцип Сен-Венана (принцип локальности) – на достаточном удалении от места приложения силы, особенности способа приложе-ния этой силы можно не учитывать;

 гипотеза Бернулли (гипотеза плоских сечений) – поперечные се-чения стержня, плоские и нормальные к оси стержня до деформации, остаются плоскими и нормальными к его оси и после деформации.

Реальный объект и расчетная схема.

Расчетная схема – это упрощенное изображение реальной конструкции, которое освобождено от ее несущественных, второстепенных особенностей и которое принимается для математического описания и расчета.

Реальный объект – исследуемый элемент конструкции, взятый с учетом всех своих особенностей: геометрических, физических, механических и других.

Моделью конструкции принято называть вспомогательный объект, заменяющий реальную конструкцию, представленную в наиболее общем виде.

Схематизация элементов конструкций (стержень, пластина, оболочка, массивное тело).

Стержнем называется тело, длина которого значительно боль-ше его поперечных размеров. Геометрическое место точек, совпадающих с центрами тяжести поперечных сечений стержня, называется продольной осью.

Элемент конструкции, ограниченный с двух сторон плоскостями, расстояние между которыми мало по сравнению с другими разм-рами, называется пластиной (рис. 1.1б). Элемент конструкции, ограниченный двумя поверхностями, отстоящими друг от друга на малом расстоянии, называется оболочкой (рис. 1.1в). Элемент конструкции, размеры которого во всех направлениях сравнимы по величине, называется массивом (рис. 1.1г).

Виды внешних сил. Объемные и поверхностные нагрузки.

Внешние силы являются мерой взаимодействия рассматриваемого тела с окружающими телами и средой. Различают объемные и поверхностные силы. Объемные силы непрерывно распределены по всему объему тел. Отметим, что к поверхностным силам относятся вес тела, силы инерции, магнитные силы. Поверхностные силы действуют на поверхности тела.

Динамические нагрузки изменяются во времени быстро, при этом в деформируемой конструкции возникают силы инерции, кото-рые необходимо учитывать при расчетах, так как они достигают зна-чительных величин.

Статические нагрузки являются постоянными, либо медленно изменяют свою величину или точку приложения (направление).

Если размеры площадки, по которой происходит взаимодействие тел, малы по срав-нению с размерами тела, то считается, что поверхностная сила прило-жена в точке и называется сосредоточенной.

Соприкосновение тел всегда происходит по некоторой площад-ке. Поэтому все поверхностные силы являются распределенными по площади.

Виды опор.

шарнирно подвижные опоры. Поперечное сечение стержня в шарнирно подвижной опоре может смещаться параллельно опорной плоскости и поворачиваться, но не может смещаться перпендикулярно к опорной плоскости. Поэтому в шарнирно подвижной опоре возникает реакция опоры АR , направленная перпендикулярно к плоскости.

шарнирно неподвижная опора. Поперечное сечение стержня, проходящее через шарнирно неподвижную опору, не может смещаться поступательно. В опоре возникает сила реакции R (рис. 1.5). Ее составляющими являются вертикальная сила B R , препятствующая вертикальному смещению, и горизонтальная сила B H, исключающая горизонтальное смещение закрепленного сечения бруса

Заделка (защемление), это такое закрепление стержня, при котором в месте крепления он не может перемещаться поступательно и поворачиваться.

Опорные реакции.

Воздействие закрепляющего элемента на стержень можно заме-нить силой, которая называется реакцией опоры.

Реакция опоры или опорная реакция – это силовой фактор, возникающий в опоре, от действия на конструкцию внешней нагрузки. В опорах, как правило, возникают реактивные силы, которые для удобства ручного расчета раскладываются на две составляющие: вертикальную и горизонтальную проекции.

Уравнения статики.

Уравнения статики

Сумма проекций всех сил на ось Y:

Здесь силы и нагрузки записаны в соответствии с правилом знаков для проекций сил.

Равнодействующая распределенной нагрузки определяется произведением ее интенсивности на длину.

Проекции сил на ось Z в данном случае равны нулю:

Сумма моментов всех нагрузок, например, относительно точки A: