ответы / ОТВЕТЫ СОПРОМАТ 4

нагрузки эпюра представляет собой параболу. Парабола должна быть выгнута навстречу распределенной нагрузке.

3.При Q < 0 изгибающий момент слева направо уменьшается. Если Q > 0, то изгибающий момент слева направо увеличивается.

4.В том сечении, где Q = 0, на эпюре должна быть точка экстремума. При q < 0 (нагрузка направлена вниз) на эпюре расположена точка максимума, а при q > 0 (нагрузка направлена вверх) – точка минимума.

Понятие о напряженном состоянии в точке. Полное, нормальное и касательное напряжения

Напряженным состоянием в точке называется совокупность напряжений, действующих на всех возможных площадках, которые можно провести через эту точку.

Рассмотрим тело произвольной формы, нагруженное самоуравновешенной системой сил .

Попробуем охарактеризовать напряженное состояние в произвольной точке тела С. С этой целью, выделим в окрестностях этой точки элементарный объём в виде куба с бесконечно малыми гранями. На каждой грани куба действуют внутренние силы, которые представим в виде трех составляющих вектора полного напряжения:

21

На невидимых гранях куба действуют такие же по величине, но противоположные по направлению напряжения. Полученные девять напряжений, называемых компонентами напряженного состояния, образуют так называемый тензор напряжений:

,

в котором, в соответствии с законом парности касательных напряжений:

+Таким образом, напряженное состояние в точке в общем случае нагружения может быть охарактеризовано шестью компонентами напряжений: тремя нормальными и тремя касательными.

22

Интегральная связь между напряжениями и внутренними силовыми факторами

Совокупность напряжений и , действующих по различным площадкам в одной точке, представляет собой напряжённое состояние в этой точке.

Связь напряжений с внутренними силовыми факторами может быть описана следующими

23

соотношениями

где A - площадь сечения; x, y- текущие координаты элементарной площадки. Условие прочности, задаваемое ограничением возникающих в сечении

максимально допускаемых значений напряжений, записывается в виде неравенства

где , - максимально допускаемые значения нормальных или касательных напряжений, определяемые материалом изделия, его термообработкой, другими влияющими на прочность

технологическими факторами.

Понятие о деформированном состоянии в точке

Деформированным состоянием в точке называется совокупность деформаций, возникающих в различных направлениях и различных плоскостях, проходящих через данную точку.

Рассмотрим элементарный объем, находящийся в условиях объемного напряженного состояния.

Под действием напряжений этот объем деформируется, в результате каждая грань изменяет свои размеры в направлении координатных осей и может получить угловую деформацию. Так, например, передняя грань принимает вид:

24

Таким образом, в направлении оси z элементарный размер dz грани получит относительную деформацию , а в направлении

осиx элементарный размер dx изменится на величину . Угол между ребрами грани изменится на величину .

Подобные деформации получат и остальные грани элементарного объема. Тогда деформированное состояние в точке определится тензором деформаций:

,

где линейные деформации

, ,

и угловые деформации

, ,.

+Свойства деформированного состояния аналогичны свойствам напряженного состояния, в частности, можно выделить три взаимно перпендикулярные оси, в системе которых угловые деформации отсутствуют. Линейные деформации, возникающие в этой системе координат, называются главными деформациями. Главные деформации нумеруют в порядке убывания .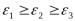

Различают линейное, плоское и объемное деформированные состояния.

25

линейное плоское объемное

Площадки главных напряжений и главных деформаций для линейноупругого изотропного тела совпадают.

Линейные и угловые деформации

Линейная деформация - характеризует изменение размеров тела. Различают абсолютную деформацию ΔL и относительную деформацию ε = ΔL/L.

Угловая деформация - характеризует изменение формы тела и чаще всего называется углом сдвига

26

3. РАСТЯЖЕНИЕ И СЖАТИЕ СТЕРЖНЕЙ. Растяжение и сжатие прямолинейного стержня. Напряжения в поперечных сечениях. Деформации при растяжении-сжатии. Коэффициент Пуассона. Закон Гука. Модуль упругости. Потенциальная энергия деформации. Испытание материалов на растяжение-сжатие. Диаграммы на растяжение-сжатие различных материалов. Механические характеристики материалов. Пластичные и хрупкие материалы. Допускаемые напряжения, коэффициент запаса прочности. Условие прочности при растяжении-сжатии.

http://mysopromat.ru/uchebnye_kursy/sopromat/rastyazhenie_szhatie/

http://cdo.bru.by/course/distan/PGS/sopromat_pgsdz/Fail/lekcher_3.pdf

Деформация– изменение формы и размеров тела под действием приложенных сил.

Растяжение и сжатие прямолинейного стержня

Осевым растяжением (сжатием) стержня называется вид нагружения, при котором в поперечных сечениях стержня возникает только продольная сила N .

Величины внутренних сил находят с использованием метода сечений и принятого правила знаков.

Продольная сила N считается положительной, если она растягивает отсеченную часть стержня (рис. 2.1), т.е. направлена по направлению внешней нормали к сечению.

Графики, показывающие, как изменяются внутренние силы в направлении продольной оси стержня, называются эпюрами внутренних сил.

27

Напряжения в поперечных сечениях

Гипотеза плоских сечений(Д.Бернулли):

Поперечные сечения стержня, плоские до деформации, остаются плоскими и после деформации. Так как продольные слои стержня деформируются одинаково, то и нормальные напряжения во всех точках поперечного сечения должны быть одинаковыми. Поэтому в любом поперечном сечении const , получаем

Следовательно

- равнодействующей напряжений.

N - продольная сила, которая возникает в поперечных сечениях стержня.

Деформации при растяжении и сжатии

Обозначим длину стержня через l, а высоту и ширину поперечного

сечения b и a . На рис. 2.3 пунктирной линией показан стержень после растяжения.

Как показывают опыты, при растяжении длина стержня увеличивается, а поперечные размеры уменьшаются. Его длина станет равной l1 , высота и ширина сечения – b1 и a1 . При сжатии

– наоборот, стержень становится короче, а поперечные размеры увеличиваются.

При растяжении стержня продольная деформация вычисляется по формуле:

28

Относительные поперечные деформации в направлении сторон с размерами b и a:

……………………………………………………………………………………………..

Деформации при растяжении-сжатии.

Рассмотрим деформации, возникающие при растяжении (сжатии) стержня (рис.6, а). Под действием силы F брус удлиняется на некоторую величину Δl называемую абсолютным удлинением, или абсолютной продольной деформацией, которая численно равна разности длины бруса после деформации l1 и его длины до деформации l

Отношение абсолютной продольной деформации бруса Δl к его первоначальной длине l называют относительным удлинением,

или относительной продольной деформацией:

При растяжении продольная деформация положительна, а при сжатии – отрицательна. Для большинства конструкционных материалов на стадии упругой деформации выполняется закон Гука (4), устанавливающий линейную зависимость между напряжениями и деформациями:

где модуль продольной упругости Е, называемый еще модулем упругости первого рода является коэффициентом пропорциональности, между напряжениями и деформациями. Он характеризует жесткость материала при растяжении или сжатии (табл. 1).

29

Коэффициент Пуассона. Закон Гука.

Законом Гука: нормальное напряжение в поперечном сечении прямо пропорционально деформации: ,

-деформация, Е- модуль нормальной упругости(модуль Юнга)

По определению коэффициент Пуассона численно равен отношению поперечной деформации к продольной, взятому по абсолютной величине:

Модуль упругости.

Модуль упругости — коэффициент пропорциональности в законе Гука,

характеризующих способность тел мгновенно восстанавливать свою форму и объем после прекращения действия внешних сил

Потенциальная энергия деформации

30