1. Ввод знаменателя nngg.

2. Генерация числителя m.

Сгенерировали m= 861 и получили дробь

Разложение полученной непрерывной дроби:

_ 3684 1889 1889 1 1795 _ 1889 1795 1795 1 94 _ 1795 94 1786 19 9 _ 94 9 90 10 4	_ 9 4 8 2 1 _ 4 1 4 4 0	19+

Проверка разложения дроби в программе CoutFrac.exe

3. Ввод последнего полученного знаменателя.

Результат разложения непрерывной дроби с вычислением промежуточных дробей

4. Разложение дроби в программе.

Разложение непрерывной дроби, полученной в соответствии с вариантом, было осуществлено верно, что подтверждают результаты выполнения программы ContFrac.exe.

4. Ознакомление с выполнением квантового алгоритма Шора с помощью программы-симулятора QuantumSimulator.exe, анализ полученных результатов.

Рассмотрим процесс симуляции выполнения квантового алгоритма Шора для модуля .

Рис. 6. Запуск программы-симулятора.

Программой было выбрано целое число , количество кубит, необходимое для задания размера квантовых регистров и, соответственно, в этом случае количество состояний каждого регистра .

Рис. 7. Вычисленные программой справочные данные.

Проверим: – верное,

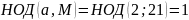– верное.

В результате выполнения квантового возведения в степень для функции 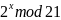для всех состояний регистра , в регистре были получены следующие значения:

{1; 2; 4; 8; 11; 16}

Рис. 8. Квантовое возведение в степень.

В результате измерения состояния регистра было получено фиксированное значение , которому соответствует суперпозиция периодических последовательностей состояний в регистре ,

Рис. 9. Измерение состояния квантового регистра .

В результате применения для суперпозиции, содержащейся в регистре , квантового преобразования Фурье, были получены следующие значения

{0; 86 - 95; 171 - 224; 342 - 351; 427 - 480}:

Рис. 10. Квантовое преобразование Фурье над регистром .

В результате измерения состояния регистра было выбрано фиксированное значение :

Рис. 11. Измерение состояния квантового регистра .

Дробь вида передана на постобработку, которая выполняется на классическом компьютере. Произведено разложение непрерывной дроби

и получены числа, которые могут рассматриваться как периоды: {1; 1; 6; 253}. Проведена попытка восстановить период.

Рис. 12. Разложение непрерывной дроби в симуляторе квантовых вычислений.

Рассчитанный период ; Степень k = r/2 = 3.

Расчет коэффициентов разложения :

Факторизация была произведена успешно. Проверяем:

.

Рис. 13. Факторизация модуля М = 21.

Следовательно, значение модуля успешно факторизовано, значит, криптосистема может быть взломана.

Таким образом, был исследован принцип работы квантового алгоритма Шора, рассмотрены отдельные этапы его выполнения и сделаны соответствующие выводы.

Вывод:

В ходе выполнения данной лабораторной работы ознакомились с квантовым алгоритмом факторизации Шора и основами квантовых вычислений, наблюдение принципа работы квантового алгоритма в симуляции.