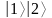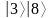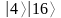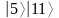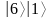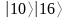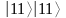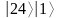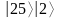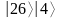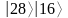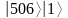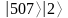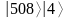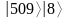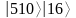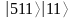МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
_____________________________________________________________________________
Кафедра информационной безопасности телекоммуникационных систем
Дисциплина «Основы криптографии с открытыми ключами»
Практическое задание 7
«Изучение квантового алгоритма Шора факторизации модуля криптосистемы РША»
Выполнила: студ. гр. .
. .
Проверил: проф. Яковлев В.А..
Санкт-Петербург
2021
Цель работы
Ознакомление с квантовым алгоритмом факторизации Шора и основами квантовых вычислений, наблюдение принципа работы квантового алгоритма в симуляции. Изучение способа факторизации модуля методом поиска периода для взлома криптосистем РША.
Программное обеспечение
Для работы используются программы QuantumSimulator.exe и ContFrac.exe из учебного каталога.
Задание
Найти период функции
,
где
,
методом простого перебора. Использовать
найденный период для факторизации
модуля
.
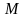Параметры
и
заданы в соответствии с вариантом из
таблицы
Ознакомиться с квантовой частью алгоритма Шора и выполнить вручную процесс квантового возведения в степень в виде записи состояния регистров для двух периодов. Выбрать любое значение
и составить для него суперпозицию
состояний регистра
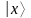.Рассчитать непрерывную дробь вида
,
где
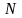– двузначный номер студента в журнале
(для номеров 01–09 взять 31–39),
– двузначный номер группы, а
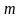– сгенерированное на основе полученного
знаменателя
в программе ContFrac.exe
число.
Ознакомиться с выполнением квантового алгоритма Шора с помощью программы-симулятора QuantumSimulator.exe, проанализировать полученные результаты и сделать выводы.
Таблица 1. Вариант задания для выполнения лабораторной работы.
№ |
|
|
6 |
6 |
21 |
Выбор |
2 |
21 |
Так как gcd(a,M) = gcd(6,21)=3 ≠ 1,
выберем а=2, тогда gcd(a,M) = gcd(2,21) =1 – условие соблюдается.
Ход работы
Найдем период функции , где , методом простого перебора.
НОД(2,21)=1,
рассмотрим
функцию
Таблица
2. Функция
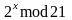
х |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
… |
|
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
210 |
211 |
212 |
213 |
… |
|
1 |
2 |
4 |
8 |
16 |
11 |
1 |
2 |
4 |
8 |
16 |
11 |
1 |
2 |
… |
Из таблицы видно, что период повторения функции r = 6.
Поскольку r – четное, то его можно представить как r = 2k.
Тогда
получим
→
Тогда, используя формулу разности квадратов, запишем
→
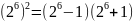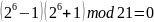
С
помощью алгоритма Евклида мы можем
найти числа p и q как
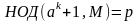и
.
Для r = 6:
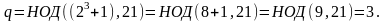
Проверяем:
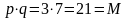
Выполним квантовое возведение в степень для двух периодов.
Для
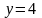составить суперпозицию состояний
регистра
.
Для
данного варианта М=21,
М2=441.
Тогд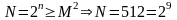а
,
а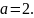
состояние
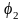будет иметь вид:
.
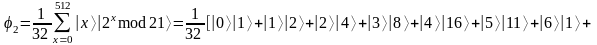
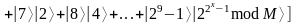Тогда
каждому фиксированному состоянию
регистра 
,
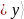
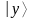соответствует последовательность
значений регистра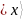 
(Таблица 3):
Таблица 3. Состояния регистров
|
|
|
|
|
|
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
|
|
|
|
|
|
… |
… |
… |
… |
… |
… |
|
|
|
|
|
|
После
измерения состояния регистра
в соответствии с заданием мы получили
фиксированное состояние
,
которому соответствует 
последовательность
значений х
вида:
,
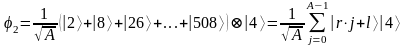Таким образом, было рассмотрено состояние регистров на этапе выполнения квантового возведения в степень и получена суперпозиция состояний в регистре , соответствующих фиксированному состоянию регистра – .
Рассчитаем непрерывную дробь вида
,
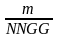где
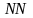– номер студента по варианту (для
номеров 01–09 взять 31–39),
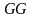– номер группы, а
– сгенерированное на основе полученного
знаменателя
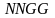в программе CoutFrac.exe
число.
Номер студента из группы №84 по журналу 06, то есть в соответствии с заданием для данного варианта знаменатель непрерывной дроби имеет вид 3684. Запустим программу CountFrac.exe и выберем вариант «Сгенерировать числитель»:
