Zadachi_Matan_10-11

ТИПОВЫЕ ЗАДАЧИ

к математическому анализу

2011-2012 уч. г.

1. Найти пределы последовательностей.

   1	2	3
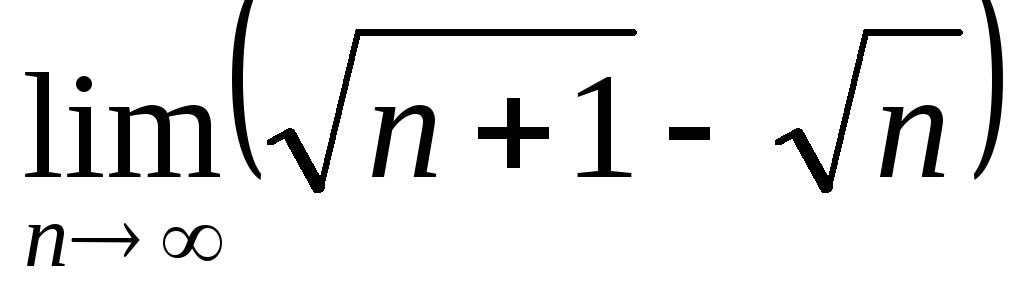
   а)	а)	а)
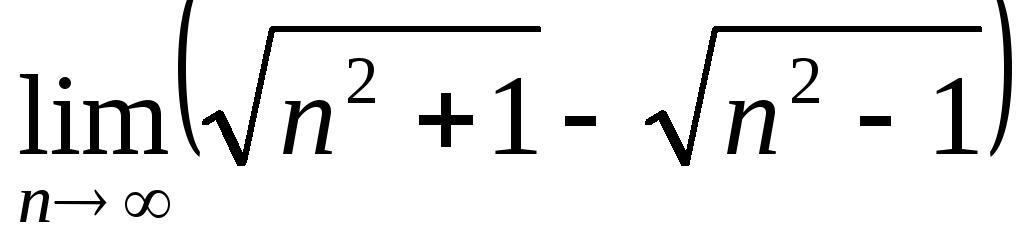
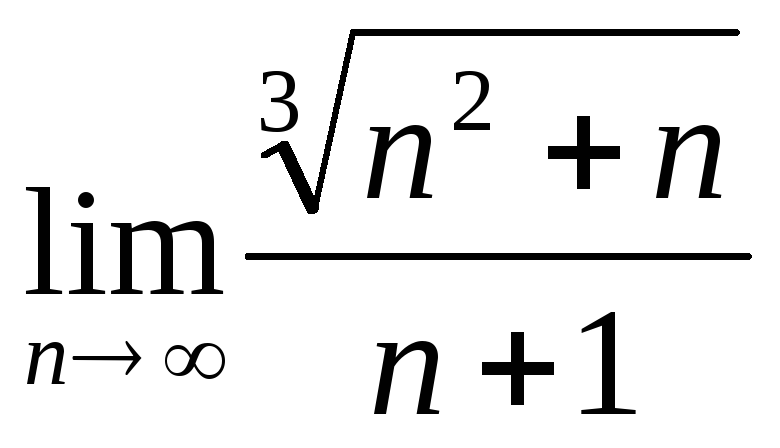
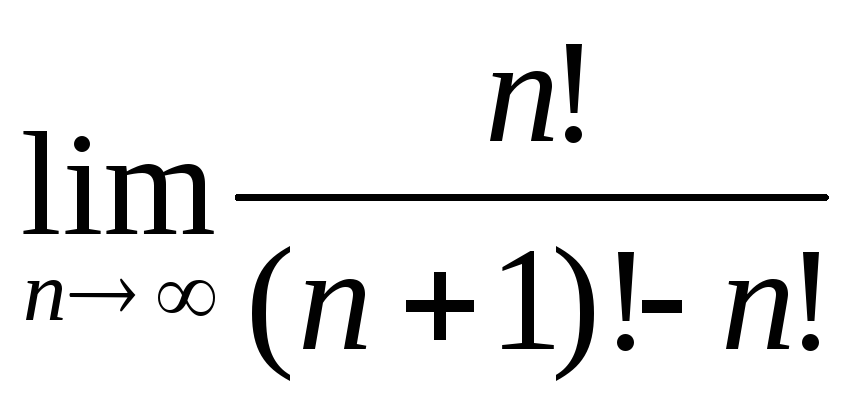
   б)	б)	б)
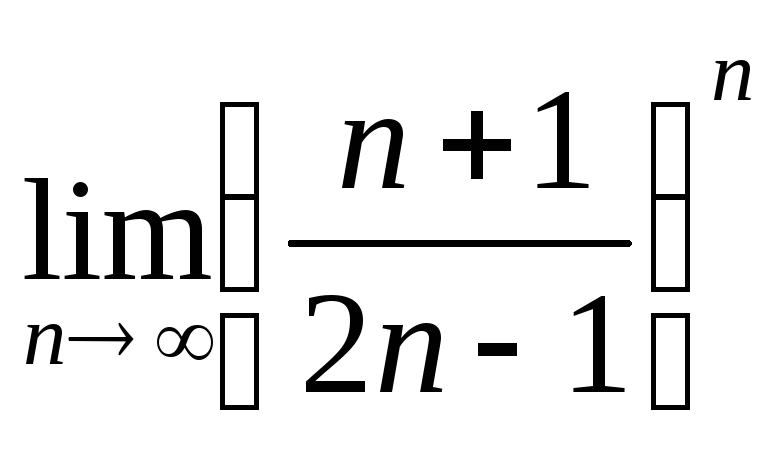
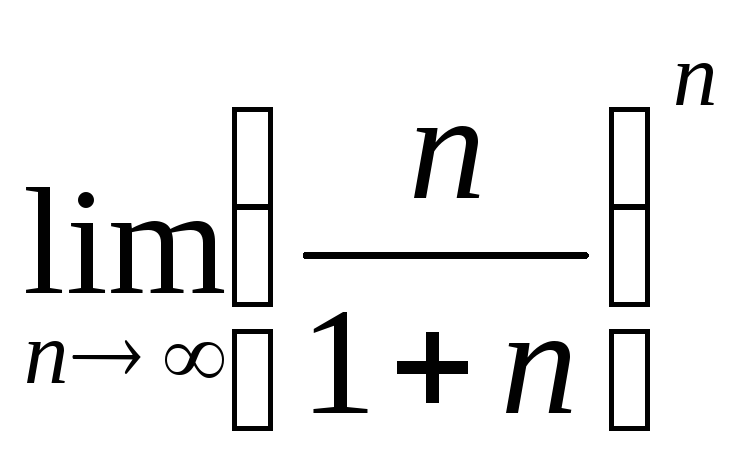
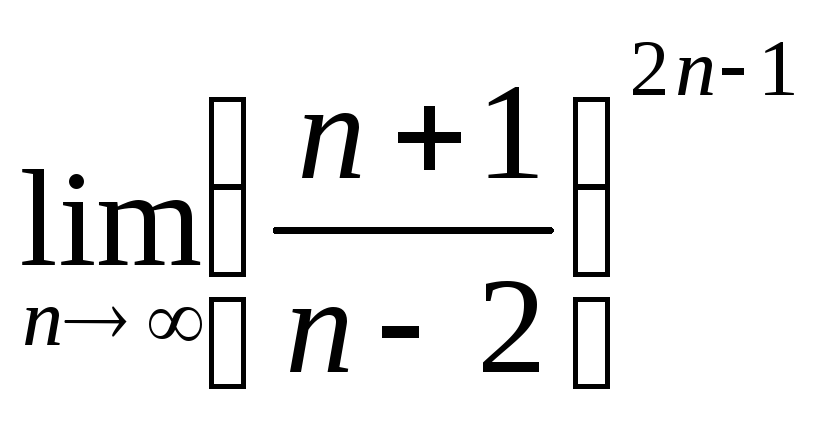
   в)	в)	в)

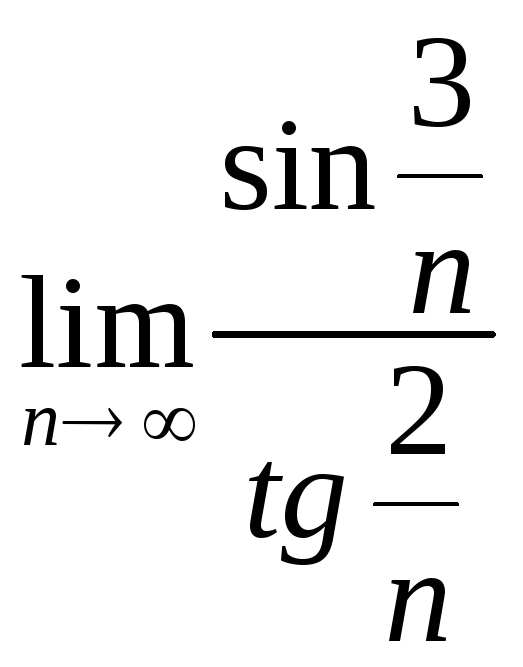
2. Найти пределы функций.

   1	2	3
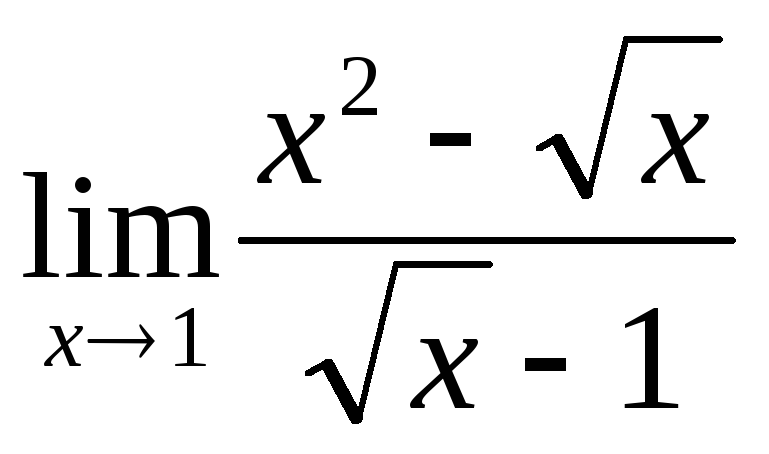
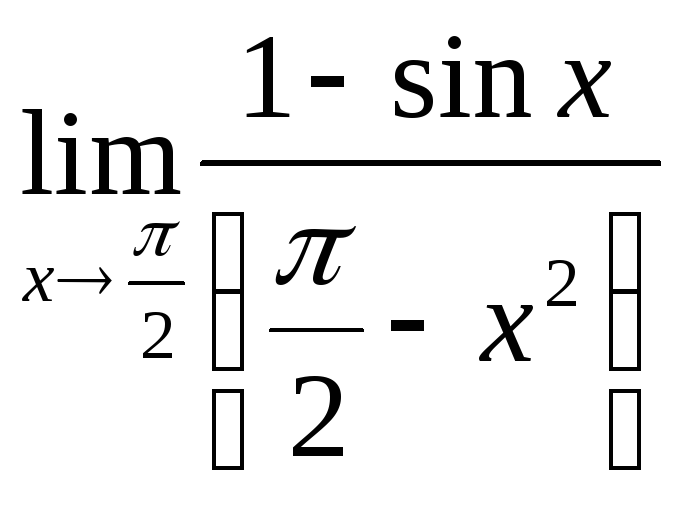
   а)	а)	а)
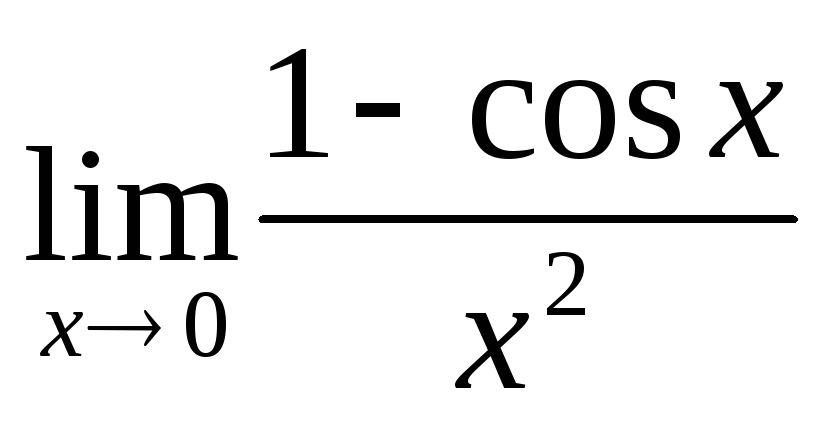
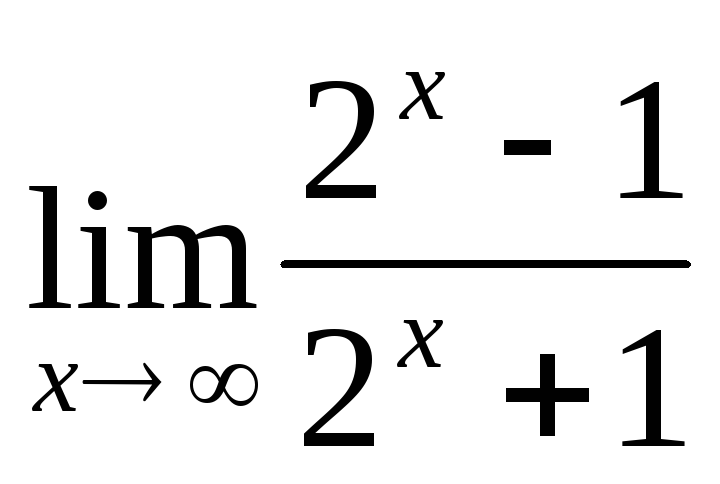
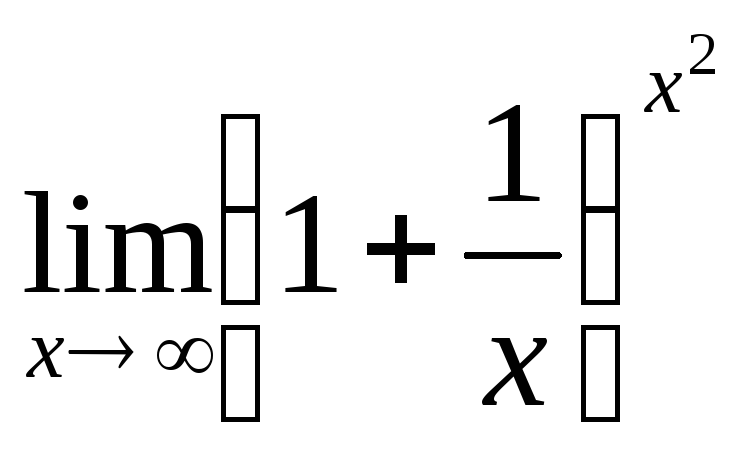
   б)	б)	б)
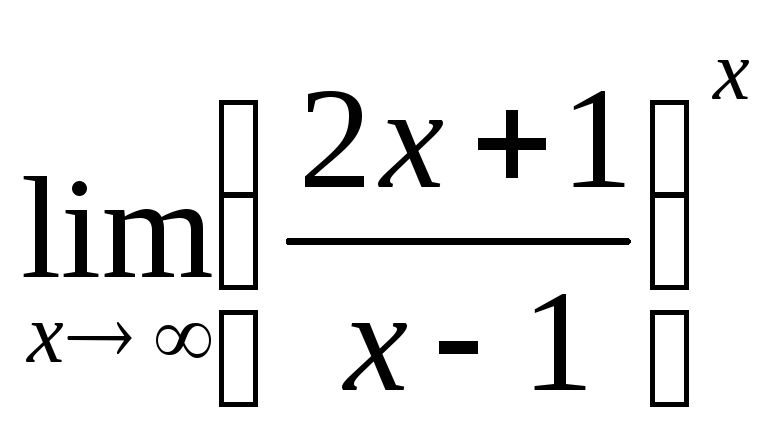
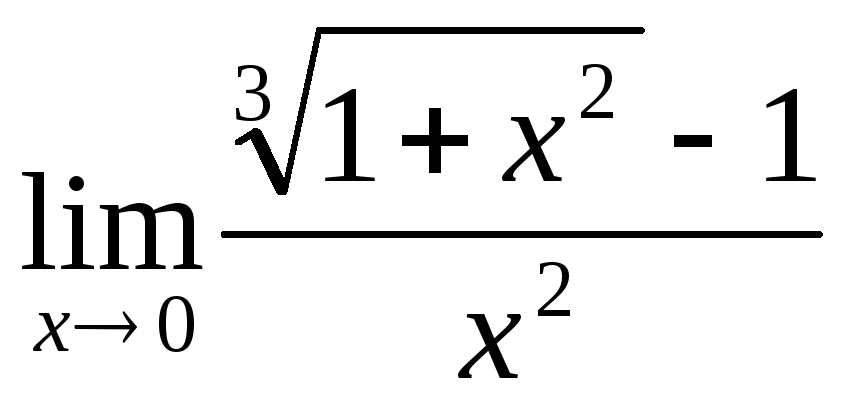
   в)	в)	в)

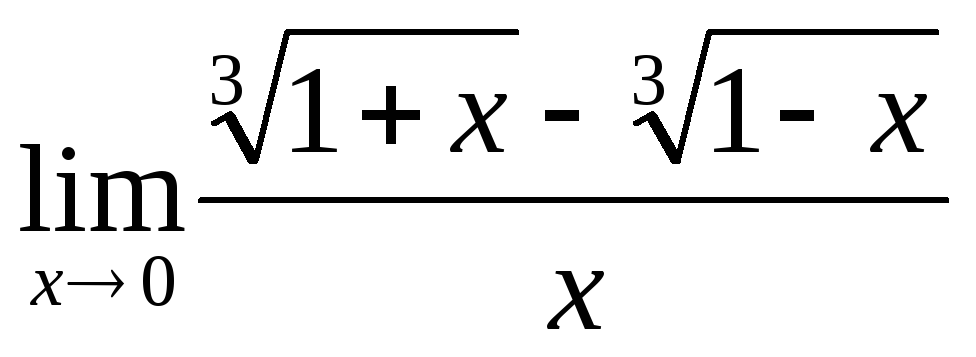
3. Построить график функций

   1	2	3
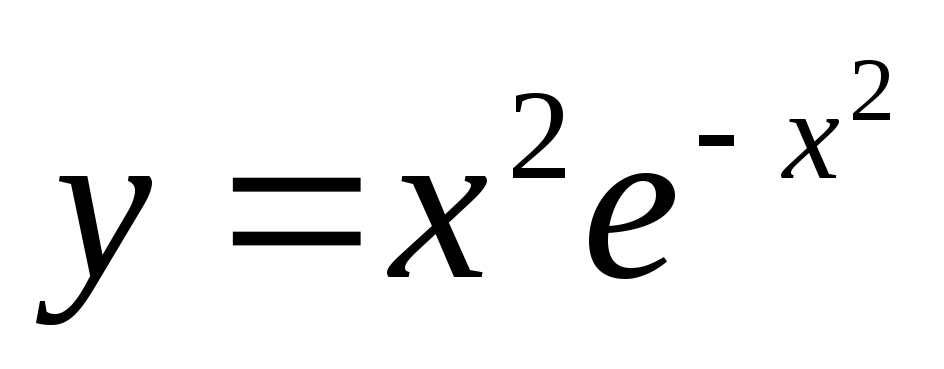
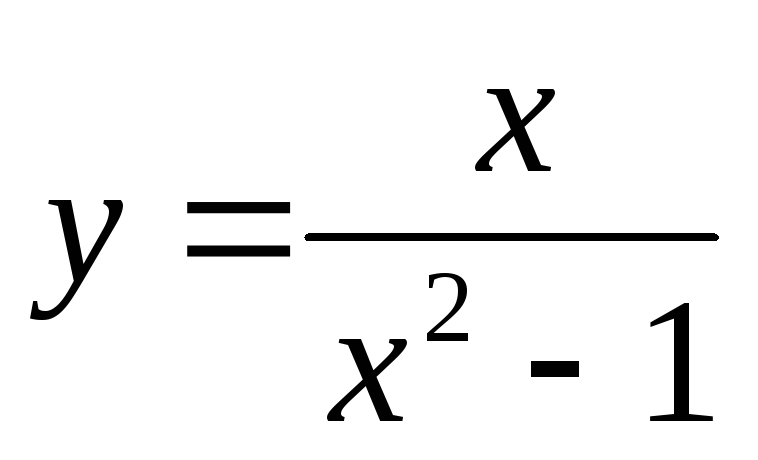
   		а)

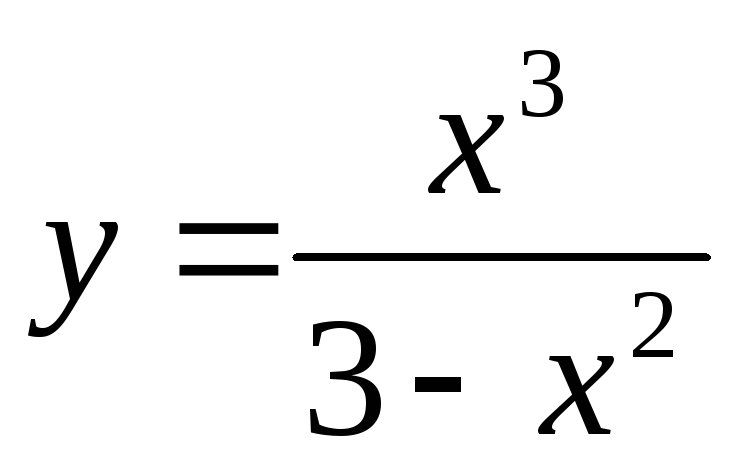
4. Вычислить интегралы.

   1	2	3
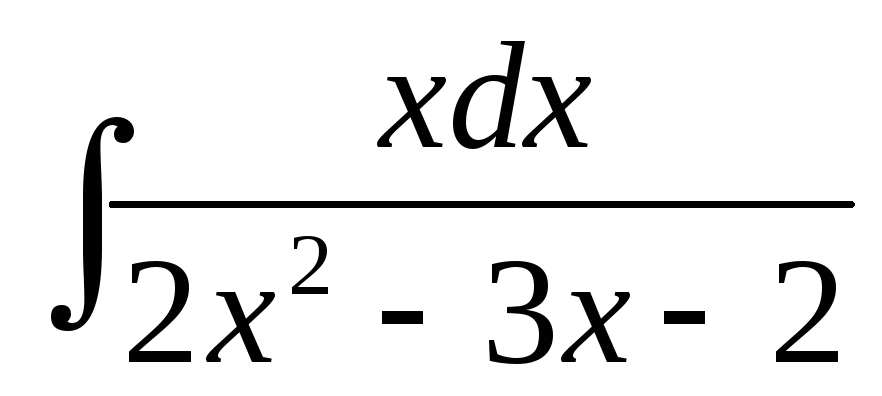
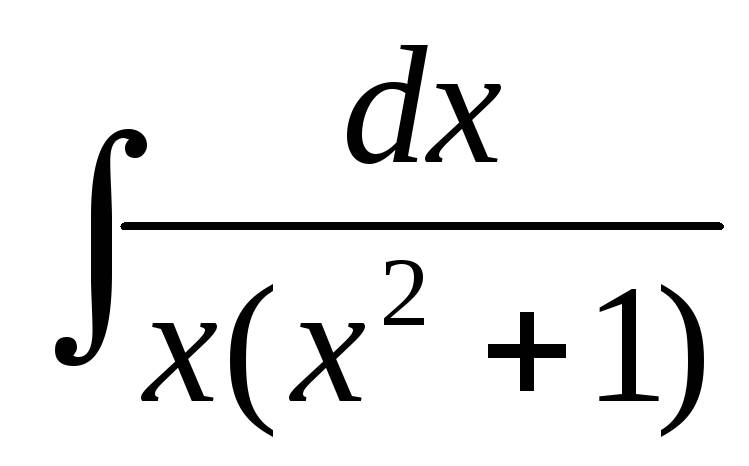
   а)	а)	а)
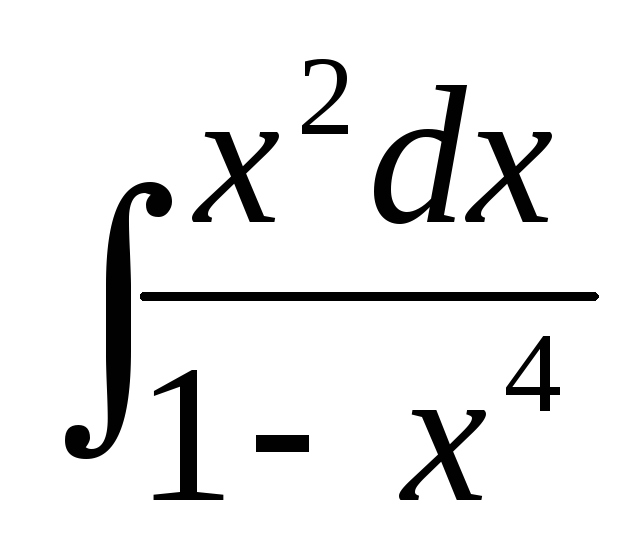
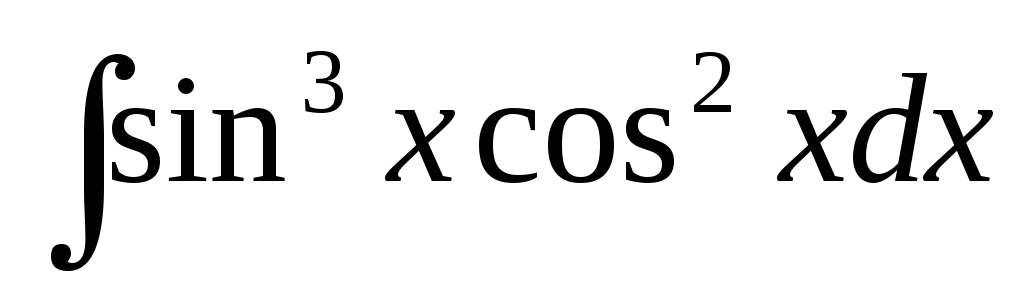
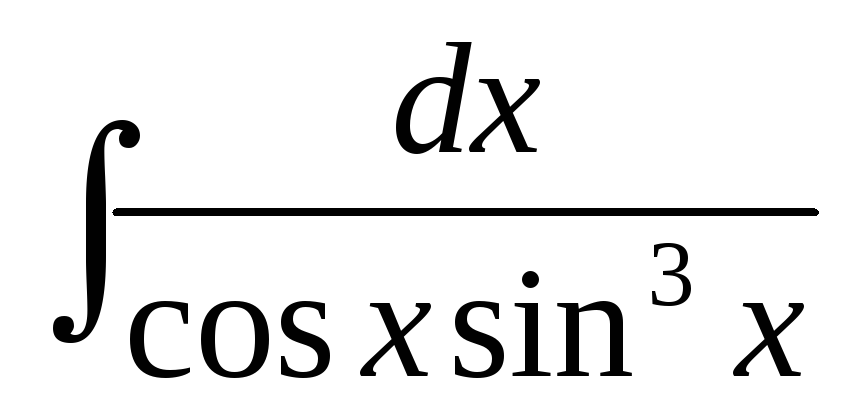
   б)	б)	б)
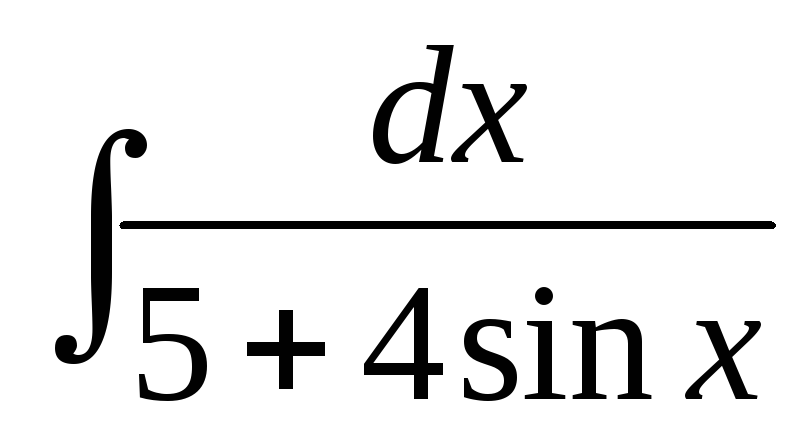
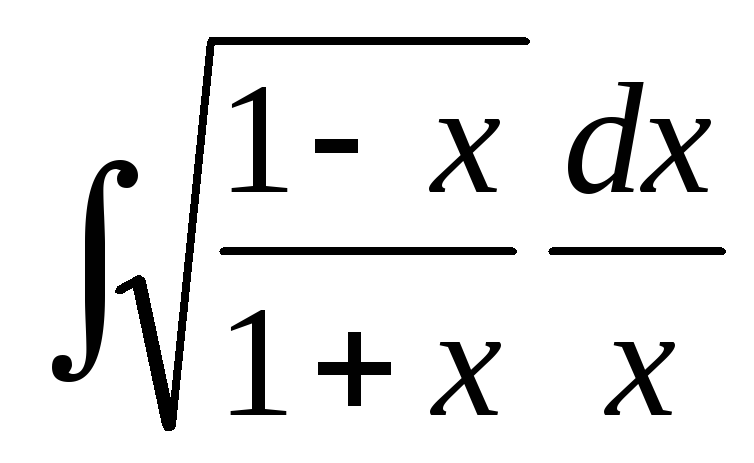
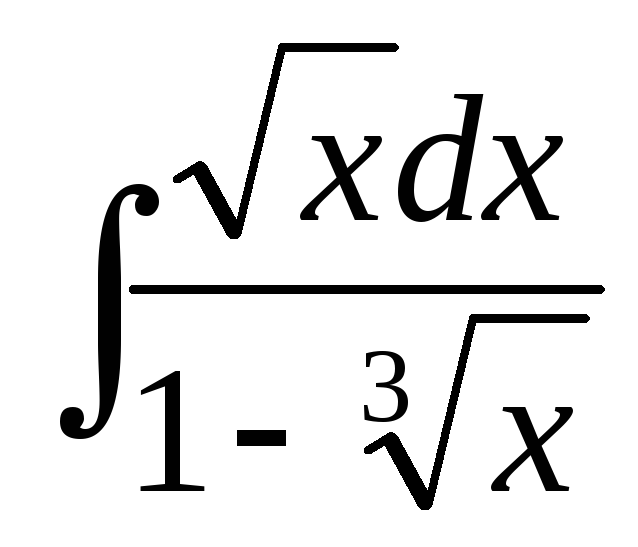
   в)	в)	в)

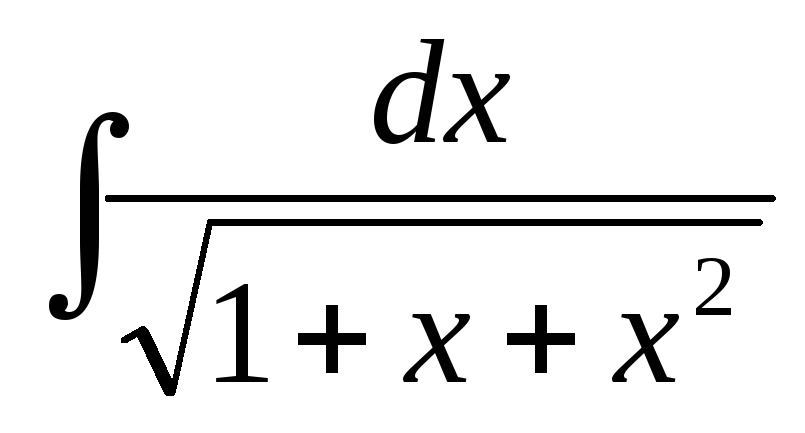
5. Вычислить интегралы

   1	2	3
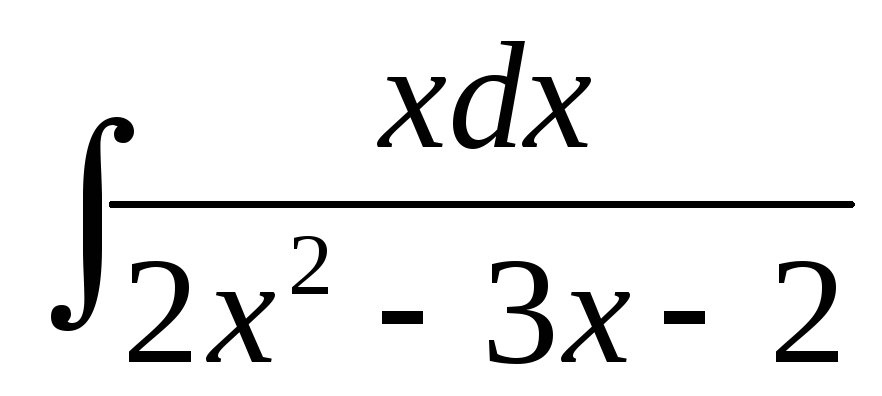
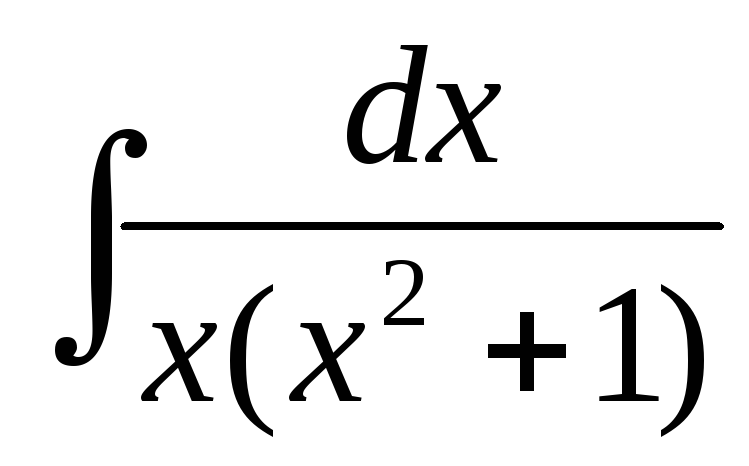
   а)	а)	а)

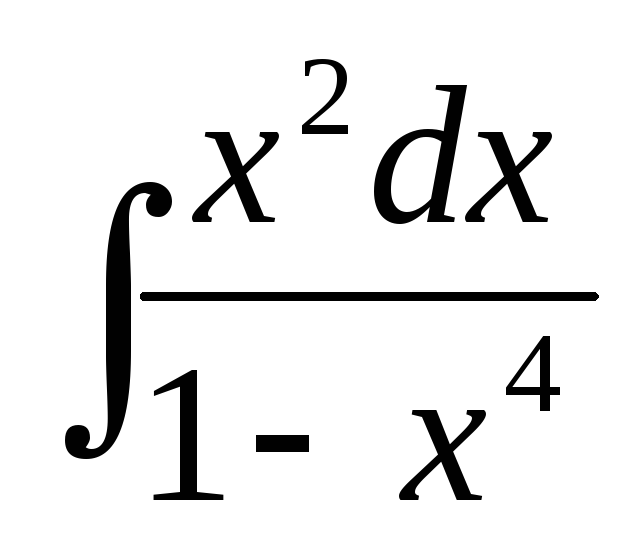
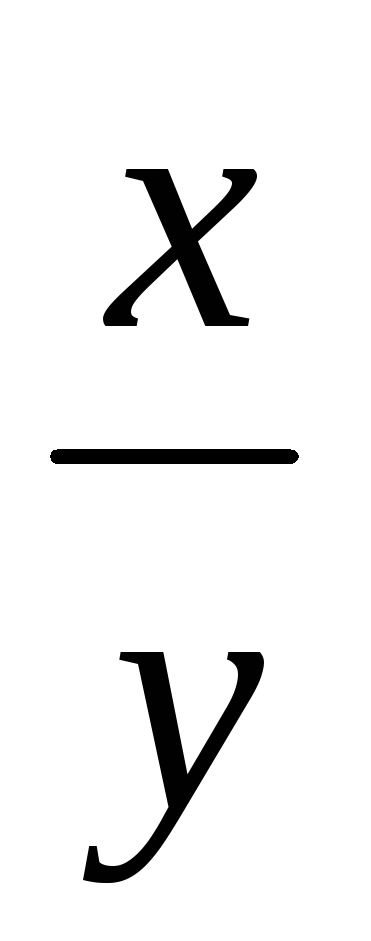
6. Найти

   1	2	3
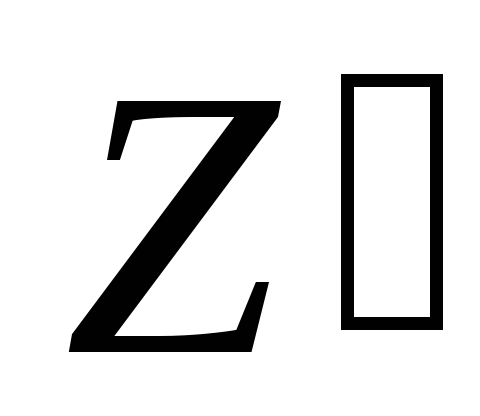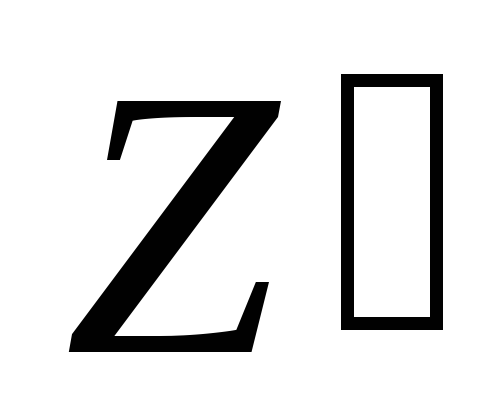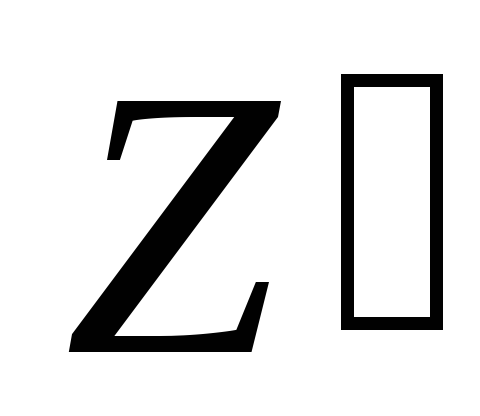   а) х, y - ? Z=arctg	а) х, y - ? Z=ln tg	а) dz - ? Z=
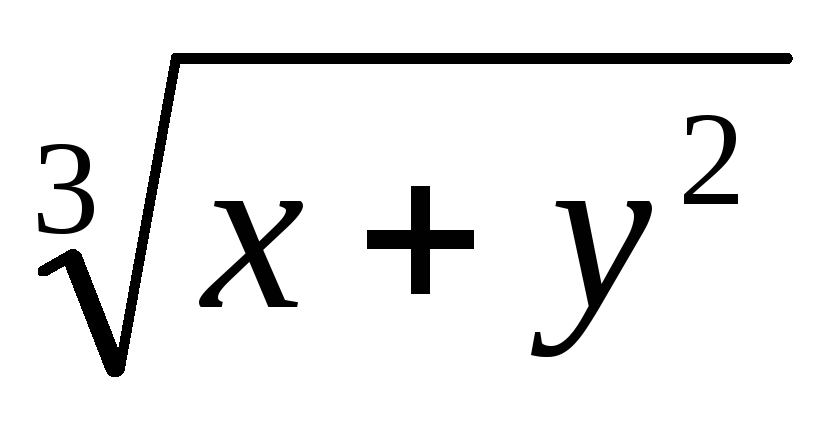
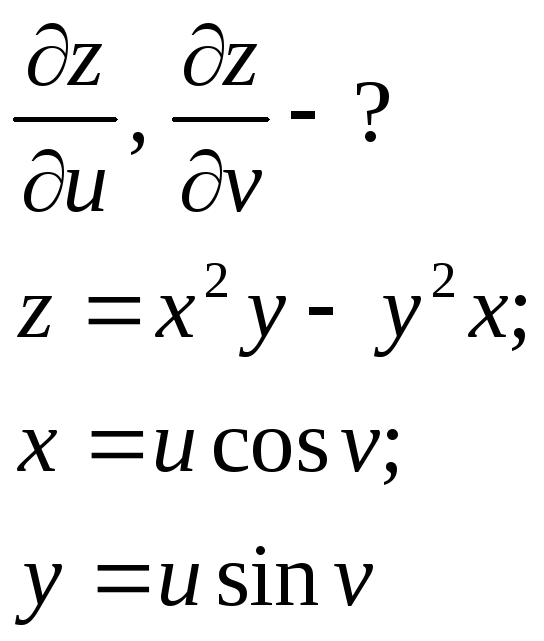
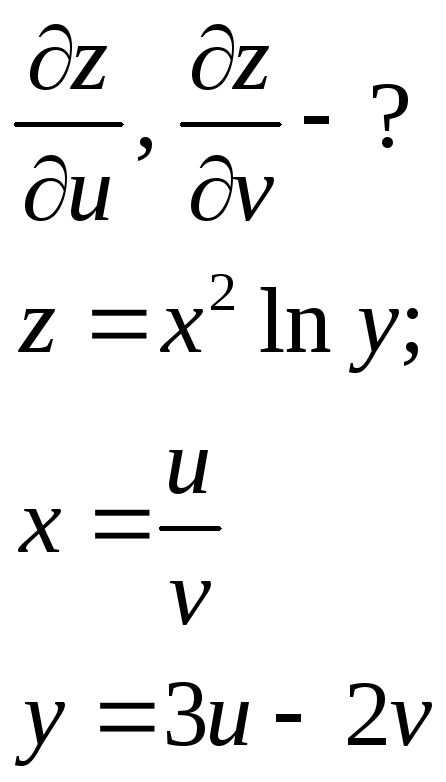
   б)	б)	б)

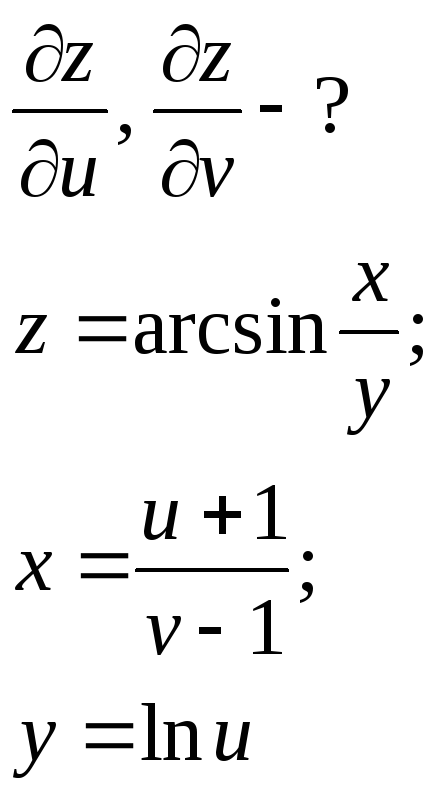
7. Вычислить:

1	2	3
а) , где (D)– область, ограничения параболами у=х2; у2=х.	а) , где (D)– область, ограничения формулами х=2, у=х, ху=1.	а) , где (D)– область, ограничения прямыми х=0, у = ; у = х

8. Вычислить криволинейный интеграл

1	2	3
а) , где (С)– контур треугольника АВО с вершинами А(1,0), В(0,1), О(0,0).	а) где (С)– верхняя половина эллипса х=аcost, y=bsint, пробегаемое по часовой стрелке.	а) где (С)– первая арка циклоиды х = а(t-sint), y=a(t-cost).

9. Решить дифференциальное уравнение:

1	2	3
а)	а)	а)

10. Решить дифференциальное уравнение:

1	2	3
а)	а)	а)

11. Вычислить интеграл

    1	2	3
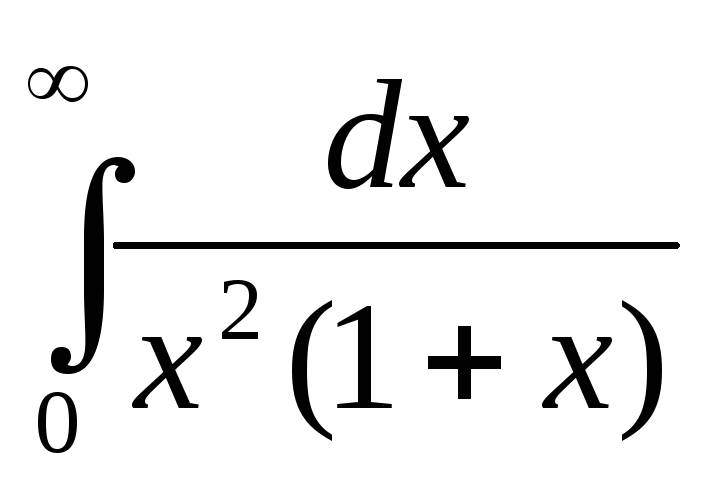
    а)	а)	а)

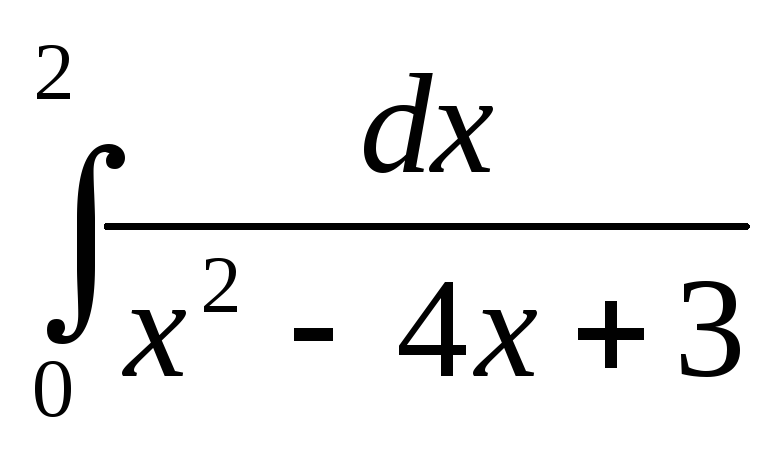
12. Исследовать ряды на сходимость:

    1	2	3
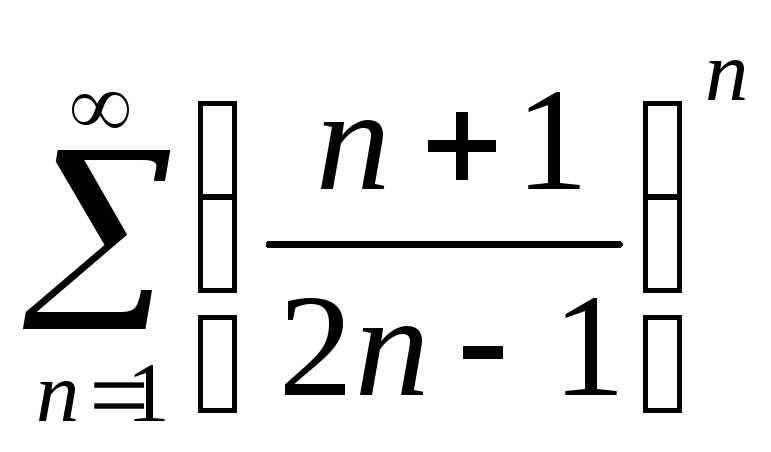
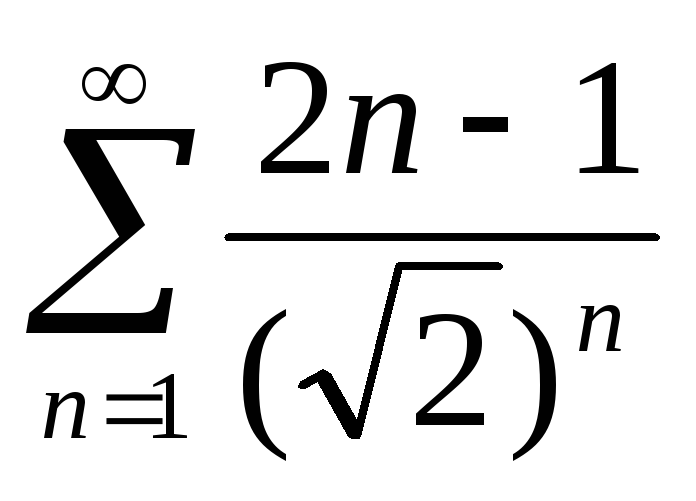
    а)	а)	а)
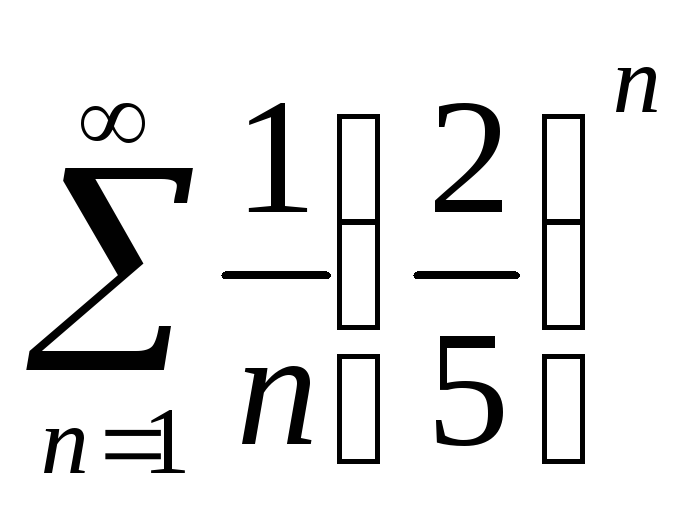
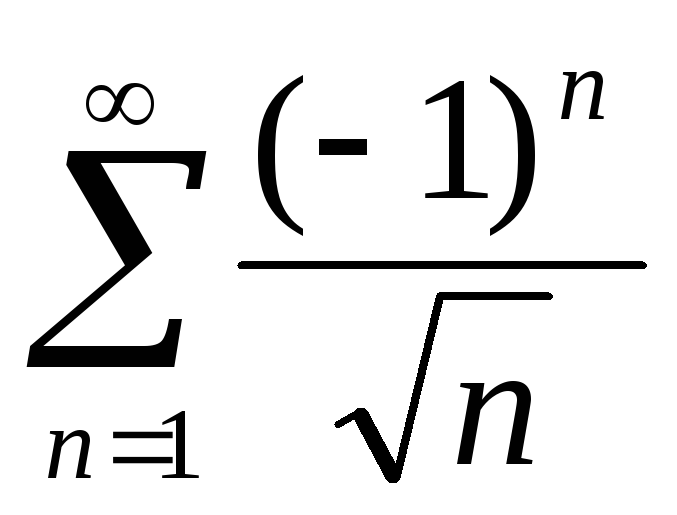
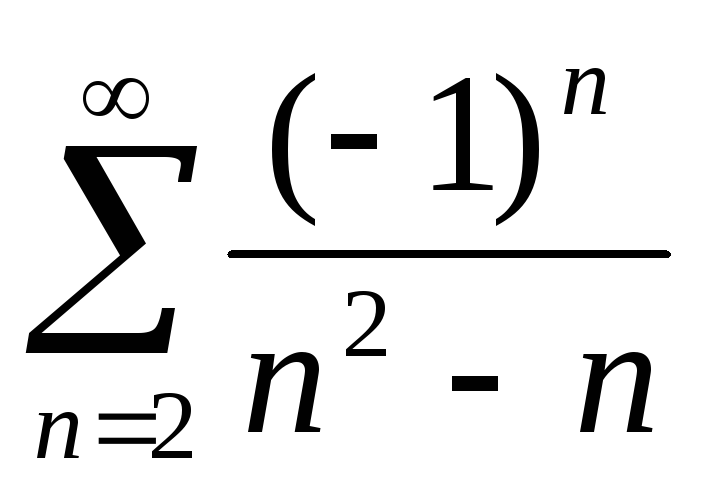
    б)	б)	б)
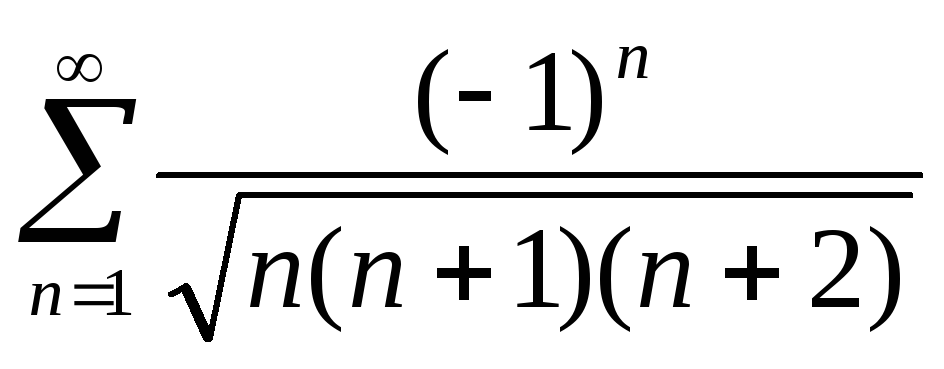
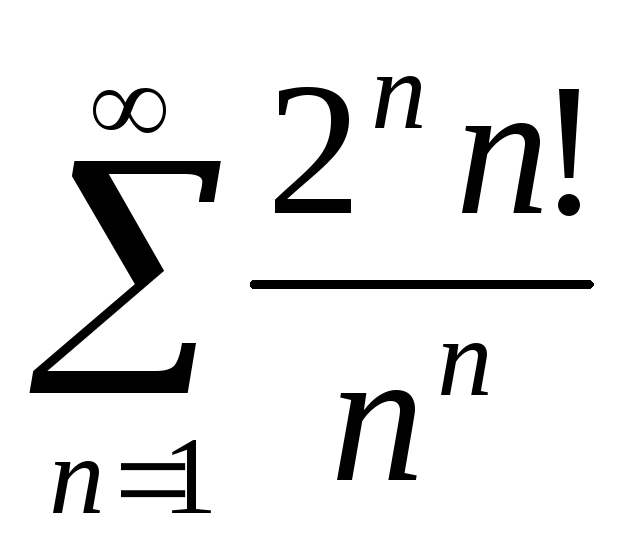
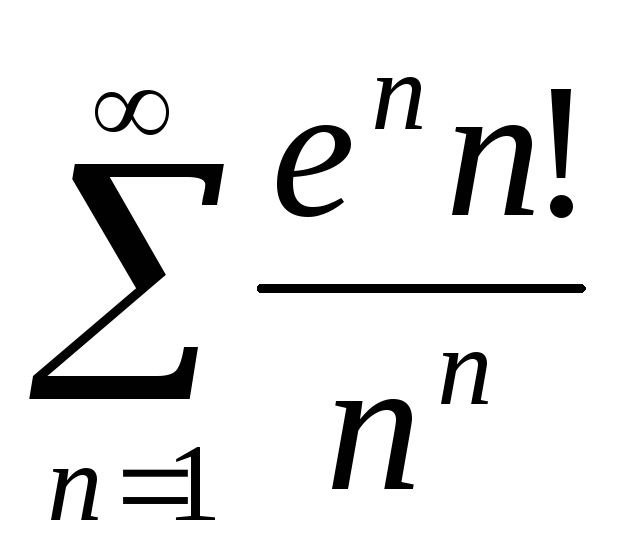
    в)	в)	в)

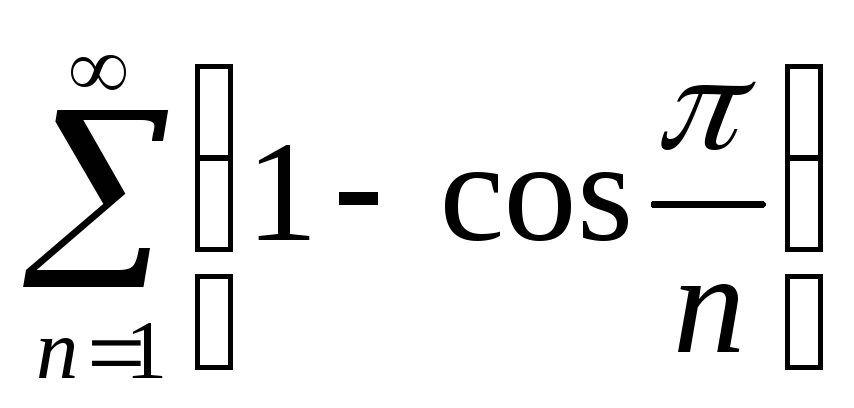
13. Разложить функцию в степенной ряд по степени х и указать интервалы, в который эти разложения имеют место

    1	2	3
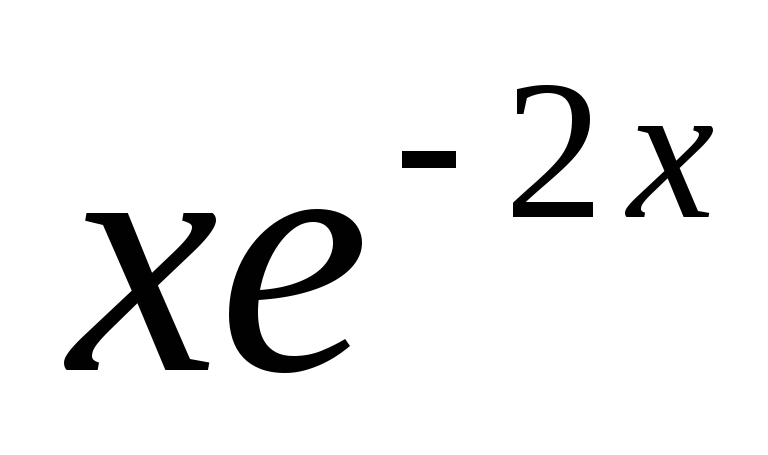
    а) y = arcsinx	а) y =	а) y = sin3x+xcos3x

1	2	3
а) Доказать эквивалентность замкнутого круга и открытого круга того же радиуса	а) Доказать, что если расстояние между любыми двумя точками множества Е на прямой больше единицы, то множество Е конечно или счетно.	а) Доказать эквивалентность плоскости и замкнутого квадрата на плоскости

15. Привести пример несчетного множества, все элементы которого изолированные/

1	2	3
а) Найти угол поворота и коэффициент искажения масштаба в точке z0=-2i при отображении	а) Дана действительная часть u(x,y)=x2-y2-x аналитической функции f(z) (z=x+iy)	а) Если возможно, найдите f(z)? Если f(z)=еxcosy+iexsiny

17. Вычислить:

    1	2	3
    а) 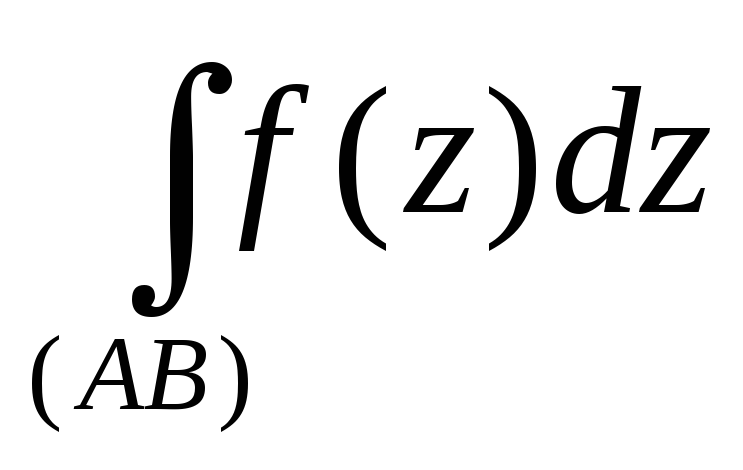, где f(z)= y+1-x i; (АВ) – отрезок прямой, соединяющий точки А=1 и В=-i.	а) 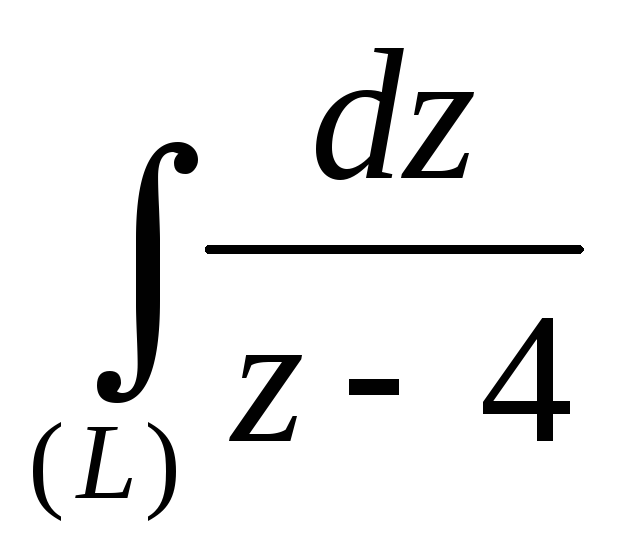, где (L) – эллипс, х=3cost y=2sint.	а) 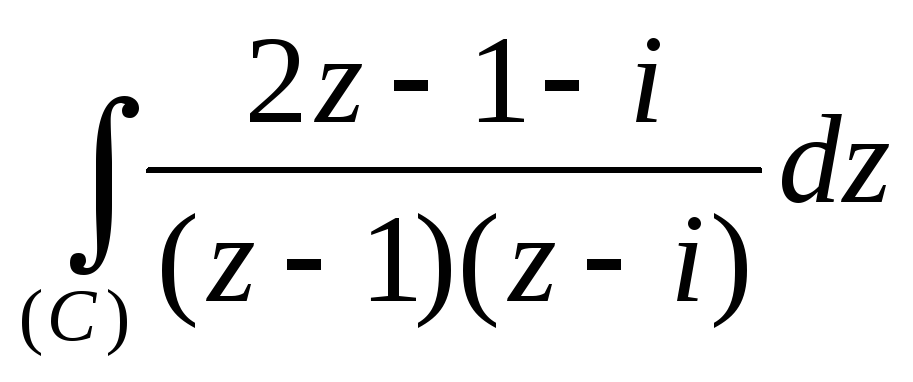, где (С) – окружность |z|=2.

1	2	3
а) Разложить в ряд Лорана по степени Z функцию в окрестности точки z=	а) Найти вычет функции .	а) Найти , где - замкнутый контур, внутри которого находятся точки , .

19. Пусть имеются следующие данные о распределении работников по стажу работы. Найти средний стаж работы и среднее квадратическое отклонение. Изобразить графически данное распределение.

Стаж работы, лет	До 1	1-5	5-10	10-20	20-40	всего
Число работников	8	12	16	14	10	60

20. Нормально распределенная случайная величина задана дифференциальной функцией: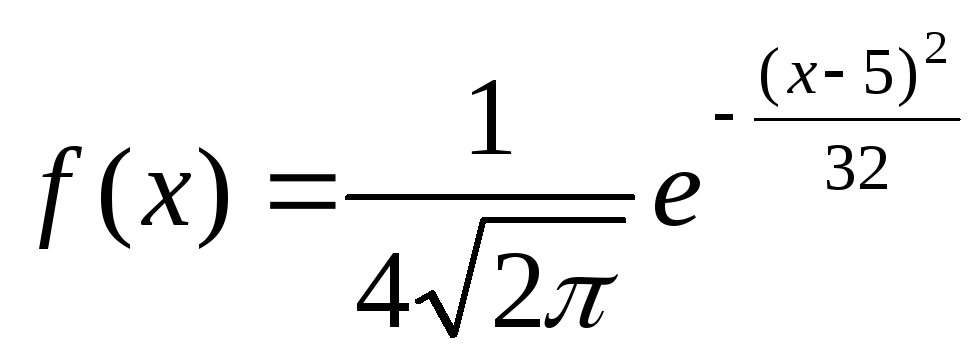. Определить вероятность попадания случайной величины в интервал (3;9).

21. В сеансе одновременной игры в шахматы с гроссмейстером играют 10 перворазрядников, 15 второразрядников. Вероятность того, что в таком сеансе перворазрядник выиграет у гроссмейстера, равна 0,2, для второразрядника – 0,1. Случайно выбранный участник выиграл. Какова вероятность того, что это был второразрядник?

22. Вероятность получить высокие дивиденды по акциям на первом предприятии - 0,2, на втором – 0,35, на третьем – 0,15. Определить вероятность того, что акционер, имеющий акции всех предприятий, получит высокие дивиденды только на одном предприятии.