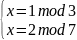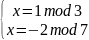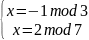Лабораторные и практики / 03_ЛР / 03_ЛР
.docxМИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ
ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ
«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»
(СПбГУТ)
_____________________________________________________________________________
Кафедра информационной безопасности телекоммуникационных систем
Дисциплина «Основы криптографии с открытыми ключами»
Лабораторная работа 3
«Тестирование простых чисел»
Выполнила: студ. гр. .
.
Проверил: проф. Яковлев В.А..
Санкт-Петербург
2021
Цель работы:
Закрепить знания, полученные на лекциях курса “Основы криптографии с открытым ключом“ по разделам: “Квадратичные вычеты” и “Генерирование и тестирование простых чисел”.
Ход работы:
Задание 1
Рассчитаем вероятность попадания на простое число при случайном генерировании чисел разрядности l=100, 300, 500 и 1000 при помощи следующей команды:
l:…..;
lg(x) := log(x)/log(10);
EstimateProb:2*(9*l-10)/(9*l*(l-1)*lg(10));

Вероятность попадания на простое число: 89/4455=1,99%

Вероятность попадания на простое число: 269/40365=0,66%

Вероятность попадания на простое число: 449/112275=0, 39%

Вероятность попадания на простое число: 899/449550=0,19%
Для проверки теста Ферма сгенерируем необходимое количество случайных 3-х разрядных чисел при помощи команды: U:100+random(900); и отберем среди них не менее 3 нечетных чисел m, среди которых должно быть одно простое числа. Сгенерируем не менее 5 случайных 2-х разрядных чисел a при помощи команды: U:10+random(90).
числа m: |
числа a: |
где 191 – простое число
|
|
Произведем проверку чисел m на простоту, используя тест Ферма при помощи команды: power_mod(a,m-1,m);

Программа выдала результат, что число 191 простое, а числа 429 и 585 составные.
Можно сделать вывод, что тестирование произведено верно. При использовании теста Ферма вероятность ошибки тестирования будет равна 1/2. Но стоит отметить, что тест Ферма не работает на числах Кармайкла.
Произведем тестирования числа Кармайкла m=561 по методу Ферма. Для этого сгенерируем необходимое количество случайных 2-х разрядных чисел a’ взаимно простых с 561, используя команды: gcd(a’,561);
|
|
|
Проверим число 561, используя тест Ферма
|
|
В ходе проверки программа показала, что число 561 простое, однако оно составное (3*11*17=561).
Можно сделать вывод, что данный тест нельзя использовать для чисел Кармайкла.
Произведем тестирование на простоту одного из чисел m и число Кармайкла 561, по методу Миллера–Рабина при помощи команды:
m:533;
f:0;
a:m-1;
u:random(m-2);
x:0;
while mod(a,2)=0 do (
f:f+1,
a:a/2);
printf(false,"a:~d,",a) ;
printf(false,"f:~d,",f) ;
x:power_mod(u,a,m);
for i:0 step 1 thru f do (
printf(true,"i:~d, x: ~d;",i,x),
x:mod(x^2,m));
|
|
Результат выполнения программы: число 561 составное. |
|
1) |
|
|
|
Результат выполнения программы: число 191 простое. |
|
Так как число m=191 прошло тест на простоту один раз, повторим расчет еще четыре раза. Если хотя бы в одном случае число m не пройдет тест, то оно составное .
2) |
|
|
|
|
|
Результат выполнения программы: число 191 простое. |
|||
3) |
|
|
|
Результат выполнения программы: число 191 простое. |
|
4) |
|
|
|
Результат выполнения программы: число 191 простое. |
|
5) |
|
|
|
Результат выполнения программы: число 191 простое. |
|
Xисло 191 простое с вероятность ошибки p=1/45=0,0009765625.
Тест Миллера — Рабина позволяет эффективно определить, является ли число простым или составным, однако данный тест - вероятностный. Вероятность ошибки равна 1/4к.
Найдем несколько квадратичных вычетов u<m по mod(m), где m одно из простых 3-х разрядных чисел, используя вычисление символа Якоби (который для простых m совпадает с символом Лежандра) , при помощи следующей команды:
u:…..;m:…;
jacobi(u,m)
|
|
|
Задание 2
Распределение числа в поле GF(p) на вычеты и невычеты.
Для варианта 6: p=13,.
При С=1, |
|
Проверка:
|
При С=2, |
|
Проверка:
|
При С=3, |
|
Проверка:
|
При С=4, |
|
Проверка:
|
При С=5, |
|
Проверка:
|
При С=6, |
|
Проверка:
|
При С=7, |
|
Проверка:
|
При С=8, |
|
Проверка:
|
При С=9, |
|
Проверка:
|
При С=10, |
|
Проверка:
|
При С=11, |
|
Проверка:
|
При С=12, |
|
Проверка:
|
При С=13, |
|
Проверка:
|
Проверим, является ли число а=(№вар+20)mod31 вычетом по модулю 17, 19. Для варианта 6: а=26.
-
1)

Проверка:

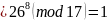 ,
вычет
,
вычет2)
Проверка:

 ,
вычет
,
вычет
Число 26 является вычетом по модулю 17 и по модулю19.
Решим уравнение
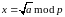
р=23, а=8 для варианта 6.
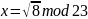

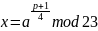
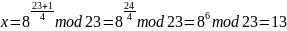
Ответ: (13; -13).
р=29, а=9 для варианта 6.
р = 29, а = 5 + 4 = 9
1) p - 1 = 22 ∙ 7
2) Символ Лежандра:
 ,
решение есть.
,
решение есть.
3) Подберем b такое, что b2-4a – невычет. Пусть b=3.
b2-1
mod
29= 8, – невычет.
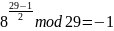 - квадратичный невычет.
- квадратичный невычет.
14 = 8 + 4 + 2
82mod 29 =64 mod 29 = 6
84mod 29 = 6∙ 6 mod 29= 7
88mod 29 = 7 ∙ 7 mod 29 = 20
(38 + 34 + 32 )mod 29 = (20∙7∙6)mod 29 = 3220 mod 29 = -1
4)
Искомый корень находим из уравнения
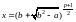
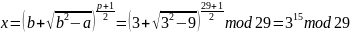
15 = 8 + 4 + 2 + 1
31mod 29 = 3
32mod 29 = 9
34mod 29 =9 ∙ 9mod 29 =(58+23) mod 29 = 23
38mod 29 = 23∙23mod 29 =(522+7 )mod 29 =7
315mod 29 = (38 ∙ 34 ∙ 32∙ 31)mod 29 = (7 ∙ 23 ∙ 9 ∙ 3) mod 29 = 26
5) Проверка:
262 mod 29 = (667+9) mod 29 = 9
(-26)2 mod 29 = 32 mod 29 = 9
Ответ: 26;-26 .
Решите уравнение
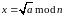
Для n=3 ∙ 7, a=16 (для варианта 6)
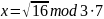
r(1;-1) |
|
Получим 4 системы уравнений:
1)
|
3)
|
2)
|
4)
|
Решение 1-й системы уравнений:
Т.к. модули m1, m2 попарно взаимно простые, система уравнений имеет единственное решение: x=x0 mod M, где М = m1∙ m2
M
= m1∙
m2
= 3∙
7
= 21
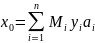
x0 = M1y1a1 + M2y2a2
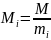
Miyi = 1mod mi
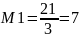 ;
;
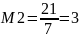
M1y1 = 1 mod m1 M2y2 = 1 mod m2
7y1 = 1 mod 3 3y2 = 1 mod 7
y1 = 1 y2 = 5
x0 = 7∙1∙1 + 3∙5∙2 = 37
x = x0 mod M
x = 37 mod 21 = 16
Решение 2-й системы уравнений:
Т.к. модули m1, m2 попарно взаимно простые, система уравнений имеет единственное решение: x = x0 mod M, где М = m1∙ m2
M = m1∙m2 = 3∙7 = 21
x0 = M1y1a1 + M2y2a2
Miyi = 1mod mi
;
M1y1 = 1 mod m1 M2y2 = 1 mod m2
7y1 = 1 mod 3 3y2 = 1 mod 7
y1 = 1 y2 = 5
x0 = 7∙1∙ (-1) + 3∙5∙ (-2) = -37
x = x0 mod M
x = -37 mod 21 = 5
Решение 3-й системы уравнений:
Т.к. модули m1, m2 попарно взаимно простые, система уравнений имеет единственное решение: x = x0 mod M, где М = m1∙ m2
M = m1∙m2 = 3∙7 = 21
x0 = M1y1a1 + M2y2a2
Miyi = 1mod mi
;
M1y1 = 1 mod m1 M2y2 = 1 mod m2
7y1 = 1 mod 3 3y2 = 1 mod 7
y1 = 1 y2 = 5
x0 = 7∙1∙1 + 3∙5∙ (-2) = -23
x = x0 mod M
x = -23 mod 21 = 19
Решение 4-й системы уравнений:
Т.к. модули m1, m2 попарно взаимно простые, система уравнений имеет единственное решение: x=x0 mod M, где М= m1∙ m2
M = m1∙m2 = 3∙7 = 21
x0 = M1y1a1 + M2y2a2
Miyi = 1mod mi
;
M1y1 = 1 mod m1 M2y2 = 1 mod m2
7y1 = 1 mod 3 3y2 = 1 mod 7
y1 = 1 y2 = 5
x0 = 7∙1∙ (-1) + 3∙5∙2 = 23
x = x0 mod M
x = 23 mod 21 = 2
Проверка:
x1: 162mod21 = 256 mod 21 = 4
x2: 52mod21 = 25 mod 21 = 4
x3: 192mod21 = 361 mod 21 = 4
x4: 22mod21 = 4 mod 21 = 4
Ответ: 𝒙𝟏 = 16; 𝒙𝟐 = 5; 𝒙𝟑 = 19; 𝒙𝟒 = 2;
Вывод:
В ходе выполнения данной лабораторной работы были закреплены знания, полученные на лекциях курса “Основы криптографии с открытым ключом“ по разделам: “Квадратичные вычеты” и “Генерирование и тестирование простых чисел”. Выполнены упражнения по нахождению доли простых чисел заданной разрядности и генерированию простых чисел при вероятностном тестировании. Найдены квадратичные вычеты по простому модулю и произведены вычисление квадратных корней из них.
Убедились в возможности быстрого тестирования многоразрядных простых чисел, а также быстрого нахождения квадратичных вычетов по простому модулю и вычисления для них квадратных корней.

 ,
,













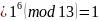 ,
вычет
,
вычет
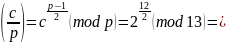
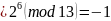 ,
невычет
,
невычет
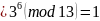 ,
вычет
,
вычет
 ,
вычет
,
вычет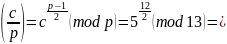
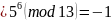 ,
невычет
,
невычет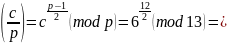
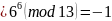 ,
невычет
,
невычет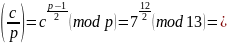
 ,
невычет
,
невычет
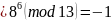 ,
невычет
,
невычет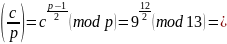
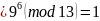 ,
вычет
,
вычет

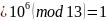 ,
вычет
,
вычет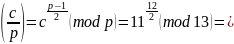
 ,
невычет
,
невычет
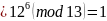 ,
вычет
,
вычет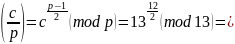
 ,
вычет
,
вычет
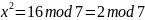 r(2;-2)
r(2;-2)